数的処理の実際の過去問を解く!
私が基礎的な問題や良問を抜粋して、
”やさしく解説”していこうと思っております。
おもに「特別区」「国税・労基」「都庁」の2019年の問題から紹介していきます。
苦手な方は必見ですよ!
『数的処理の対策・勉強方法』や『頻出テーマ』が知りたい方はこちら↓のページへどうぞ
→【受験先ごと】数的の頻出テーマ・特徴まとめ

【公務員試験】数的推理の過去問解説!
数的処理の中でも判断推理と数的推理に分かれていますが、とくに苦手な人が多いのが「数的推理」だと思います。
中学や高校の時の「数学」の基礎知識が必要な部分もあるため、苦手意識が強い方が多いようなイメージですね。
そんな方に向けて
このページでは”画像を使ってやさしく解説”できたらなと思ってます!
数的推理の問題
今回解説する問題はこちら!
公務員試験の数的推理 No.1:整数「サラダの売れた数は?」

解説


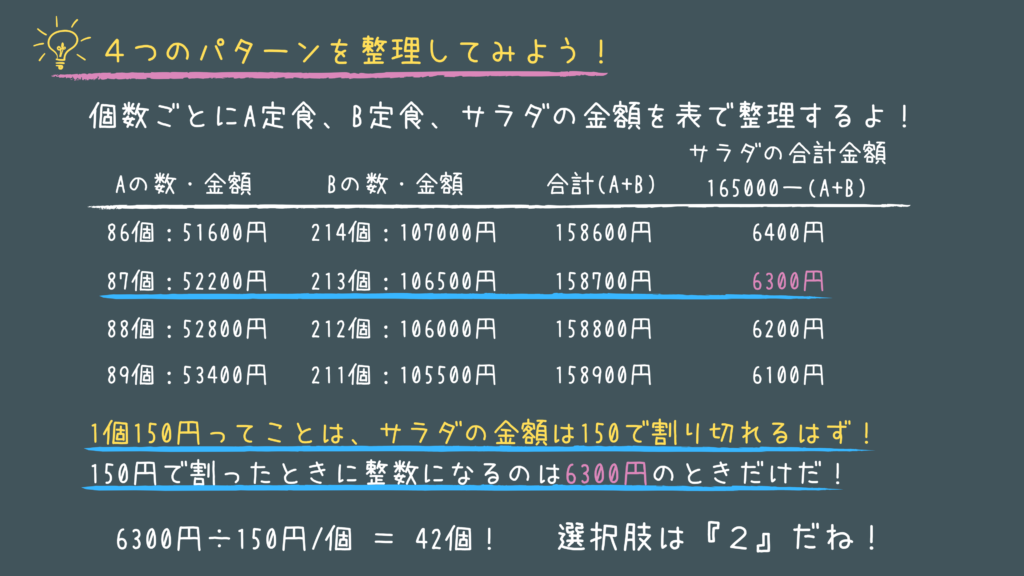
食堂でのサラダの売れた数はなぜか鉄板ですよね(笑)
これは実際に平成28年の東京都ででた問題ですが、なんと”見た瞬間に2択に絞れる”というすごい問題!
みなさんは気づきましたか?
まぁ絞り切れないので意味はないのですが、いざというとき2択に絞れるのはでかいですよね。
この問題を解くポイントはこの2つです。
- なるべく未知数(X等)は増やさない
- 選択肢を利用して解く
あとは基本的に画像に書いてある通りに解いてもらえればOKです!
真面目に計算すると法則に気づくと思いますが、Aが1個増えてBが1個減ると、合計金額は(600-500=)100円増えますよね!
こういう条件に気づくとより早く解けると思います!
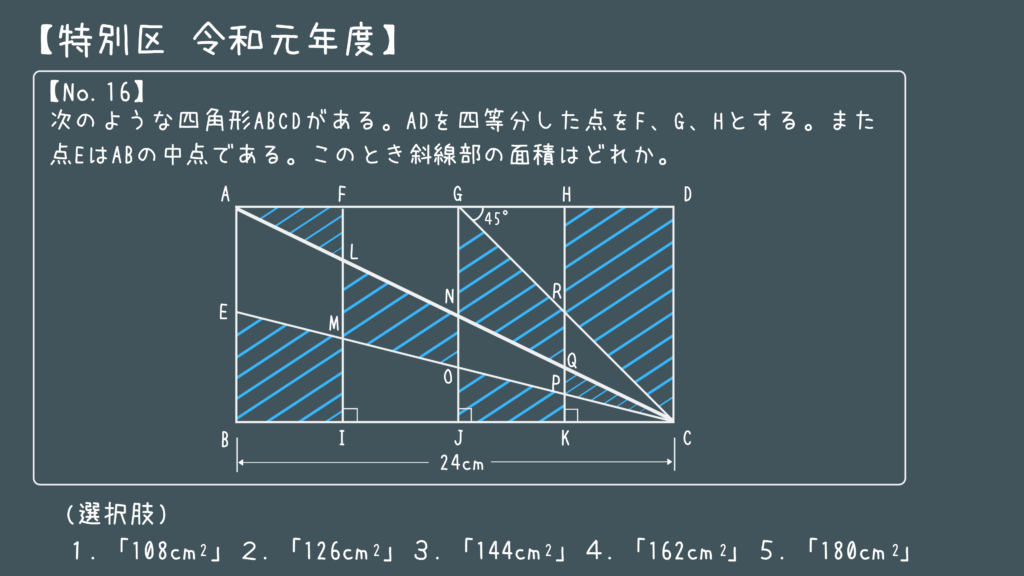
公務員試験の数的推理 No.2:面積「ある動物の模様の面積」
解説

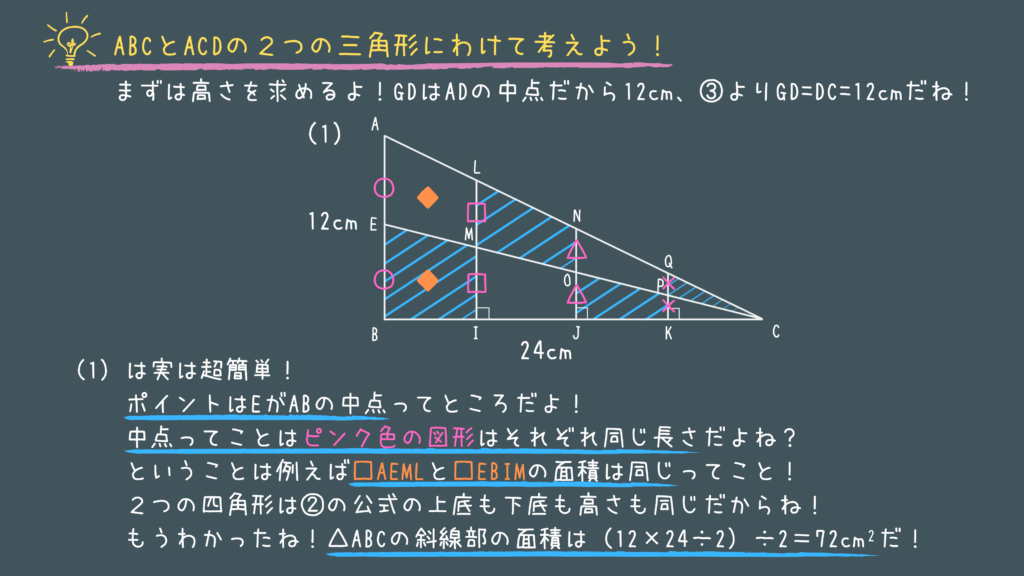
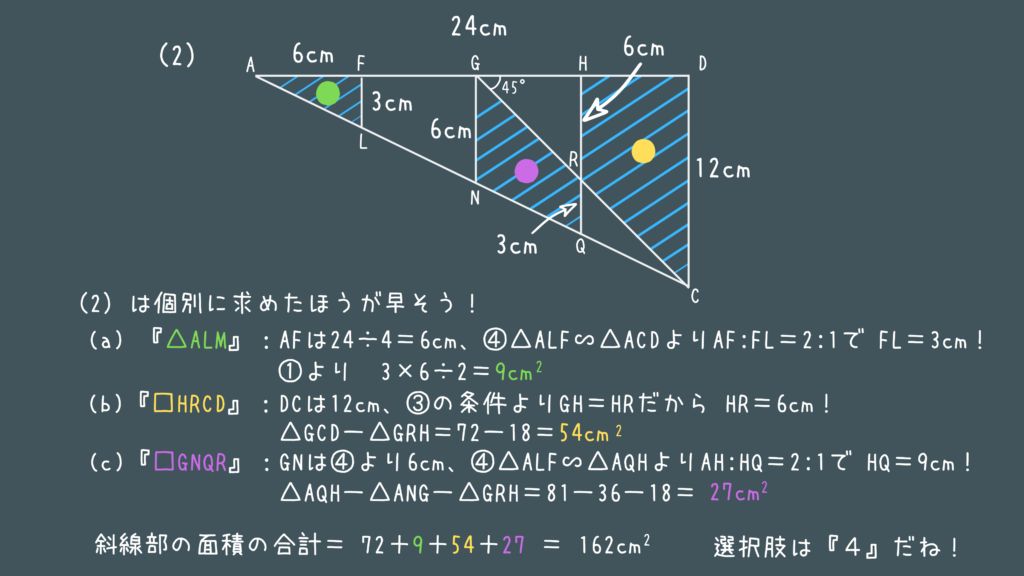
これも実際の特別区の問題です!
どこから手を付ければいいの…?ぱっと見ただけで現実逃避したくなる問題ですよね(笑)
でもある1点に気づけばこの問題は一気に簡単になります!
それは”点EがABの中点”ということです!
これに気づけば四角形ABCDを(1)、(2)のように2つにわけることができますね!
- (1)の面積は画像に記載してある知識が理解できていれば超簡単に解けます!
- (2)も三角形の面積を引き算していけばすべて求められますので、じつは簡単な問題ですね!
本番だと焦ってしまってなかなか手が出ないかもしれませんが、練習の内はこういうパターンも覚えておきたいところです!
ひとつひとつ整理して落ち着いて解いてみましょう!
公務員試験の数的推理 No.3:約数・倍数「法則に気づこう!」

解説



これは特別区の問題です。
勉強している人は簡単だけど、ノー勉の人には難しく見えるという公務員試験の鉄板問題みたいなものですね。
この手の問題には間違いなく法則性がある!
また、3と7の倍数法則はよくでますね!
1の位だけ計算すればいいので、もし忘れてしまってもその場でささっと計算しちゃいましょう!
ちなみに9は0乗から順に1,9,1,9,1,9…となっていきます!
解説では勉強のためにあえてなおしてみました!

間違ってもまともに計算なんてしてはいけません!
こういう問題には『法則』がつきもです!
公務員試験の数的推理 No.4:速さ「X町→Y町に到着するまでの時間は?」

解説


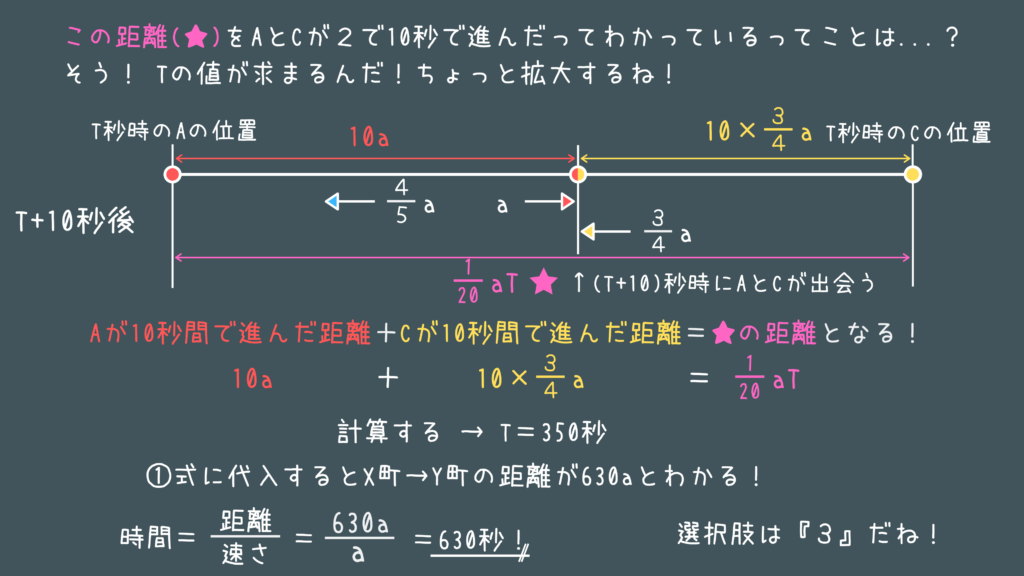
これも特別区の問題です!
やっぱり速さの問題は少し難易度が高いですよね!
逆にコツ・やり方を覚えてしまえば公務員試験の問題ならすべて解けると思いますが。
ポイントはこの点です!
- 図をかく
- 条件をきちんと整理する
- 道のり=速さ×時間
- T秒ごとT+10秒後の状態を想像してみる
この手の問題はT秒とT+10秒後などの条件を整理すればほしい値が求まるようになってますね!
道のり=速さ×時間という基礎的な部分が理解出来ていれば、整理していけば必ず解けます。
ピンクの☆の部分は”10秒間で進んだ距離”ですからね!
このように条件が明確なところに注目するとうまく解けると思います。
公務員試験の数的推理 No.5:場合の数「TOKUBETUの並び方は?」

解説

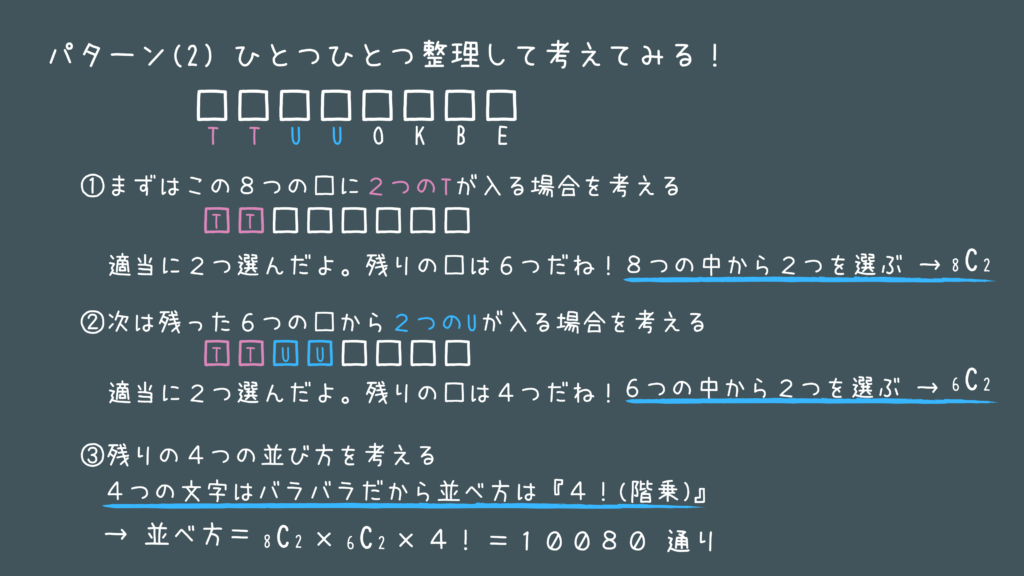

TOKUBETUなので当然特別区の問題です!
これはもうパターンを覚えるしかないです!
同じ文字を含む文字の並べ替えはよく出るのでこのパターン(1)、(2)の考え方は覚えておきましょう!
- 公式を覚える
- 余事象で解く
公式を覚えていないとなかなか最初の1歩が踏み出せないでしょう!
パターン化されているので、この際覚えてしまいましょう。
理解してしまえば簡単です!
公式で何通りあるか出しておいて、あとは余事象で解く!
図のように
(全体)-(2つのTの間に文字が1つも入らないパターン)で解けますね!
これが求めたい答えになります!
ちょっと慣れるまで大変かもしれませんが、きちんと理解しておきましょう!

公式の使い方や考え方が少し難しいですが、慣れれば簡単!
1回本気で理解してみよう!
公務員試験の数的推理 No.6:比・割合「公務員はお金の計算大事だよ」

解説


特別区の問題です!
気づかなければいけないのは”増加した金額は各社とも同じであった”という部分ですね!
ここで等式がつくれます。
また、10年前を基準にして問題を解くとスムーズだと思います!

求めるのは現在のCという点に注意しましょう!
公務員試験の数的推理 No.7:仕事算「安定のポンプ問題」

解説

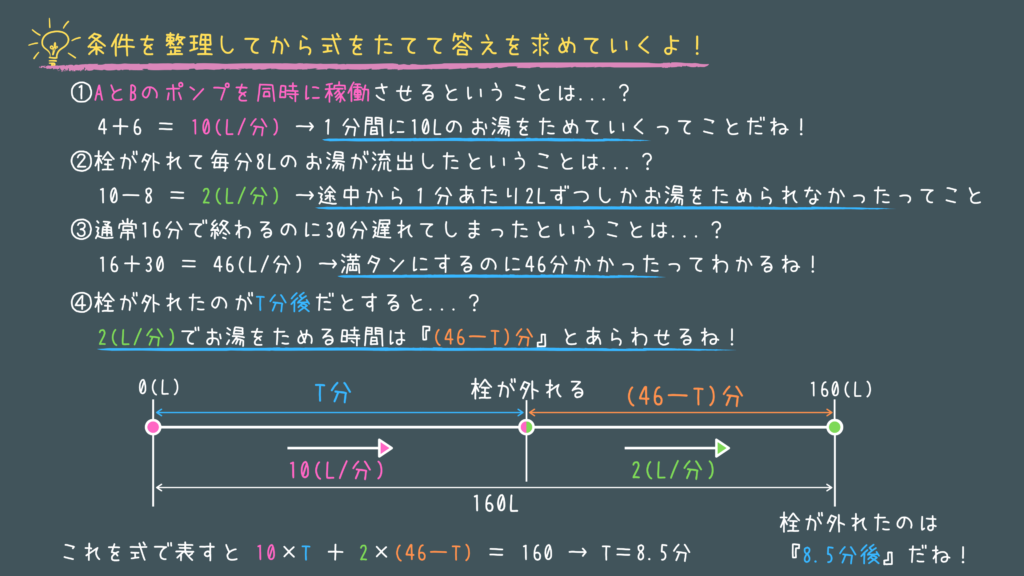
平成28年の特別区の問題がいい問題だったので紹介!
個人的にですが、仕事算には”単位を付けることをおススメ”してます!
例えば引っ越し作業なら単位を「仕事」にして、3日で引っ越しが終わるとすると1日当たりの仕事量は1/3「仕事/日」
単位が嫌いな人は↓こんなイメージ。
- 1分あたりAは4リットルの水を運ぶ
- 1分あたりBは6リットルの水を運ぶ
このように単位を意識するとごちゃごちゃせずにうまく問題が解けるかなと思います。
あとはもう算数の問題!
ひとつひとつ条件を整理して等式でむすんでいきましょう!

Bなら1分当たり6Lの水を入れれるってすぐわかるますよね!
公務員試験の数的推理 No.8:最小公倍数・最大公約数「882の約数の数は?」



ちょっと画像が多くなっちゃいましたが、特別区の実際の問題です!
画像内で徹底解説してるので、あんまりこっちでコメントはしません(笑)
かなりレベルが高い問題なので、できなくてもOKです。
882の約数の数は求められるようにしておきましょう!

素因数分解はできるようにしたいですね!
これで約数の個数を求められますので!
【公務員試験】判断推理の過去問解説!
判断推理は数学ではなく現代文・文章理解といったところがメインなので、文系の方でも嫌いな方は少ない印象。
主に苦手な方に向けて
このページでは”画像を使ってやさしく解説”できたらなと思ってます!
今回解説する問題はこちら!
ではさっそくやってみましょう!
公務員試験の判断推理 No.1:試合「PK戦」

解説

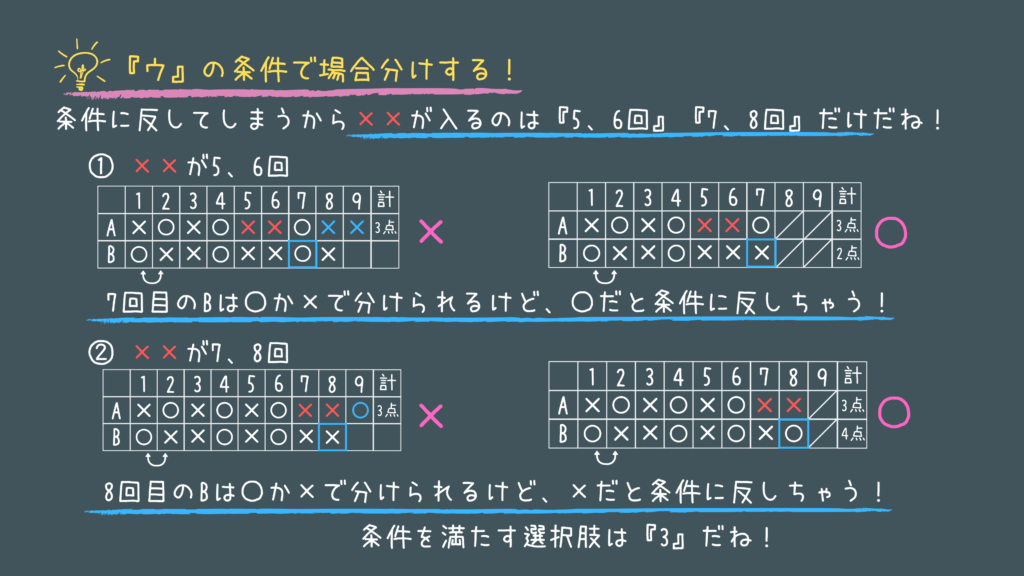
特別区の令和の1問目は試合の問題です!
わかりやすくサッカーのPK戦に内容を少し変更してみました。
ポイントは問題文の条件と「ウ」の条件の兼ね合いですね!
ここに気づけば無駄な作業をしなくて済みます!
✕✕というパターンが入るのは図の2パターンしかありませんね!

公務員試験の判断推理 No.2:暗号「実は3進法」



特別区の令和の2問目は暗号の問題です!
これはかなり難易度低めの暗号ですね!
なんせ「A・B・C・D」が与えられてますから、法則が見つけやすくなってます。
じつは3進法なので、受験生はこちらもマスターしておくと良いでしょう!

A、B、C、Dを並べ替えた段階で「3進法」だって気付きたいですよね!
この手の問題に対しては、そもそも「どうせ〇進法なんじゃないの?」って疑ってかかることが大事!
公務員試験の判断推理 No.3:対応関係「おかわり無料」

解説
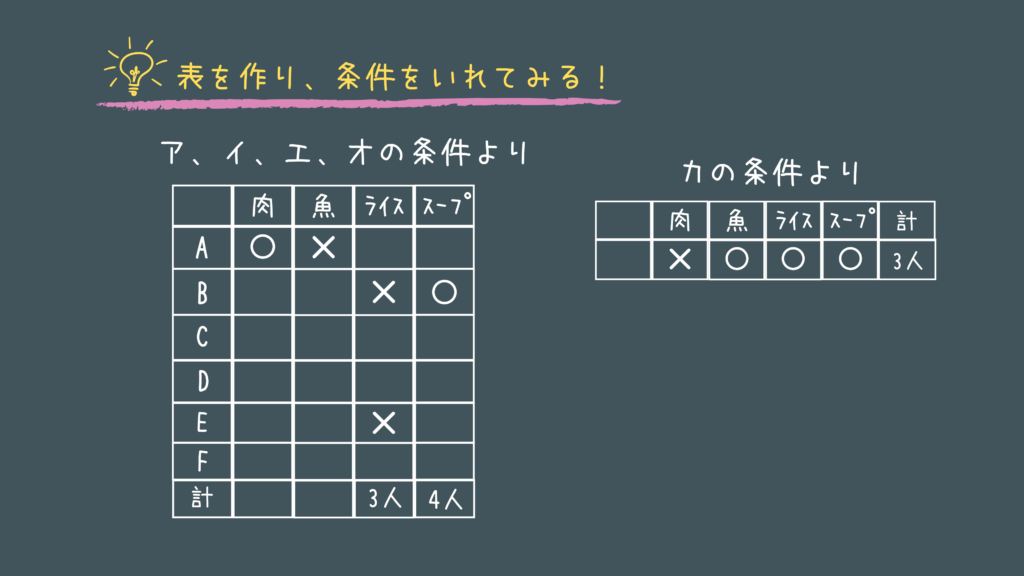
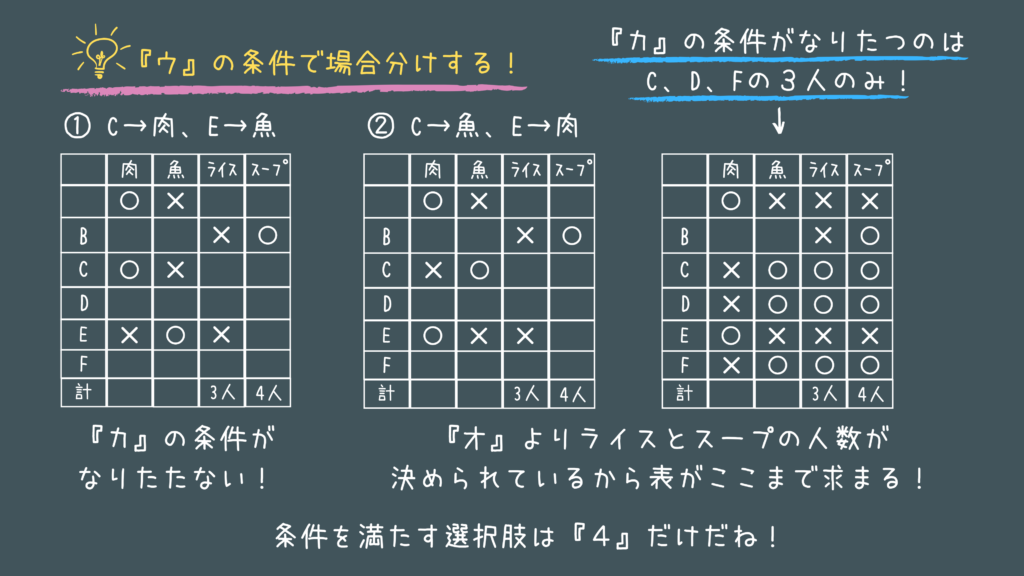
特別区の令和の3問目は安定の対応関係の問題です!
難易度自体は低めですね。
きちんとこのような表でまとめていきましょう!
やはり最後まできれいには求まらないので、きちんと場合分けを行って選択肢を選ぶことが大切です。
公務員試験の判断推理 No.4:推理「ニセ物の金メダルを探せ!」

解説



令和の特別区4問目は推理!
ニセ物の金メダル探しですね!
解法は2つ用意しましたが、この手の問題は”全体的に見る”ということが大切です!
解法2の方で解いていきたいところ。
難易度的にはそこそこ難しい問題です!

ココに気づけるようになっていきましょう!
公務員試験の判断推理 No.5:集合「ベン図の使い方」
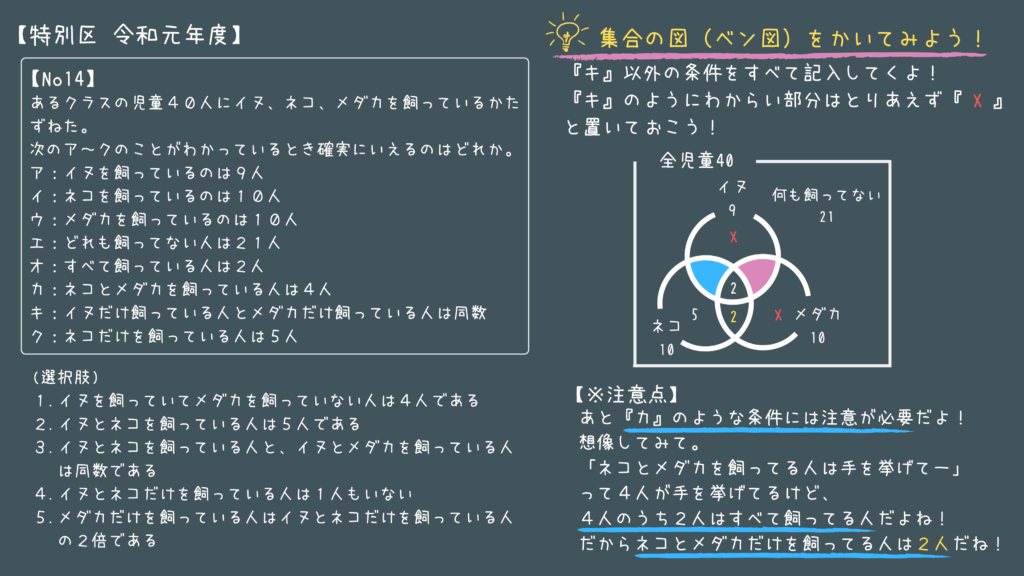

令和の特別区の5問目はベン図の問題ですね!
この手の問題で大事なのは”実際に想像してみる事”です。
2種類のみ飼っている人とすべて飼っている人が混同してしまう人が多いですからね。
あなたがクラスの生徒40人に質問してみましょう。
- ①「ネコとメダカを飼っている人は手を挙げてー」
→A、B、C、Dの4人が手を挙げた。 - ②「すべて飼っている人は手を挙げてー」
→A、Bの2人が手を挙げた
当然AとBは被ってますよね!
という事はネコとメダカのみ飼っている人はCとDの2人です。
これでもうまく理解できない人は自分がAの立場だと思って考えてみるとわかりやすいですよ!
※ABCDは適当に今作りました。
あとこの問題をとくポイントは全部で40人いて、何も飼ってない人が21人いるってことは、”何か1匹以上飼っている生徒は19人いる”ということです!
ここが最終的に問題を解くカギになりますね!
公務員試験の判断推理 No.6:数量推理「鉄板のじゃんけん」

解説


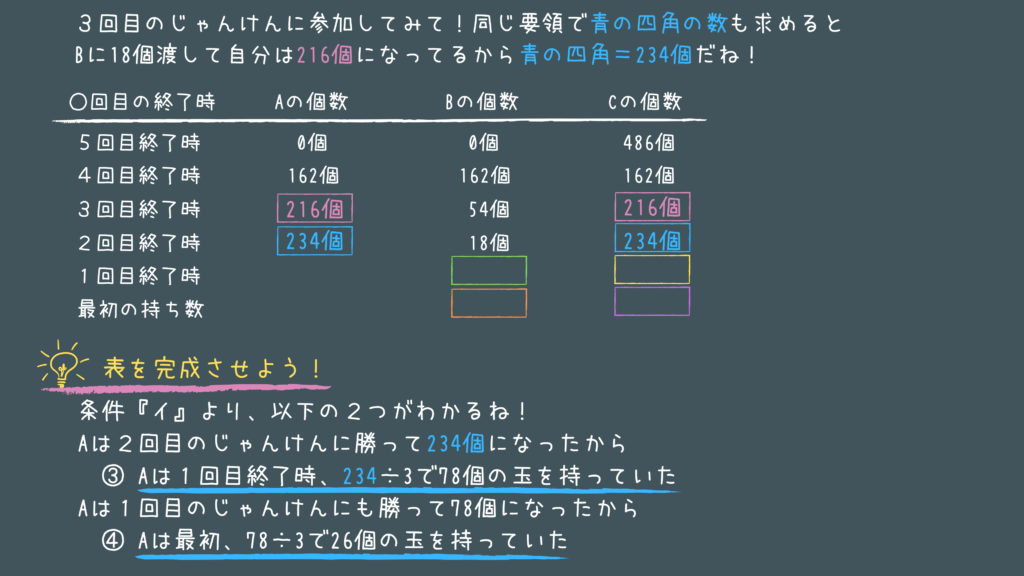

6問目は「じゃんけん」の問題ですね!
じゃんけんというと確率なんかが多いですが、この問題は数量推理です!
最近この手の問題が多いので解説してみました!
ちょっと理解するのが難しい問題だと思います。
ポイントはコレ!
- 5回目から逆算していく
- 勝ったら自分の持ってる玉が3倍になる
- 勝つ前は現在の持ち玉の1/3持っていることになる
- 負けたら勝った人の持ち玉分持っていかれる
- 負ける前は勝った人の持ち玉分多く持っていたことになる
- 実際にA、B、Cの立場になって考えてみる(自分が参加する)
とくにその人の立場になって、実際に自分が参加して考えてみるとうまく理解できます!
例えば3回目のAになってみましょう!
Bが54個もってて、Bが勝ったという事は自分の持ち玉から54個をBにあげなければいけません!
その結果自分の持ち玉は162個になったんです!
ということは負ける前は162+54=216個持っていたことになりますよね!
ひとつひとつ整理して考えると意外に簡単に解けるかもしれません。
公務員試験の数的処理「チャレンジ問題」
令和元年の国税専門官・労働基準監督官の教養試験で実際に出題された問題を5問やってみましょう!
とりあえず数的推理から5問出題します!
特別区や市役所に比べてちょっとレベルが高いので、解けなくても大丈夫ですよ!
この問題が解けたらあなたはもう合格レベル!
内容としてはこの5分野になります!
ではさっそくやってみましょう!
数的推理チャレンジ問題 No.1:「場合の数」

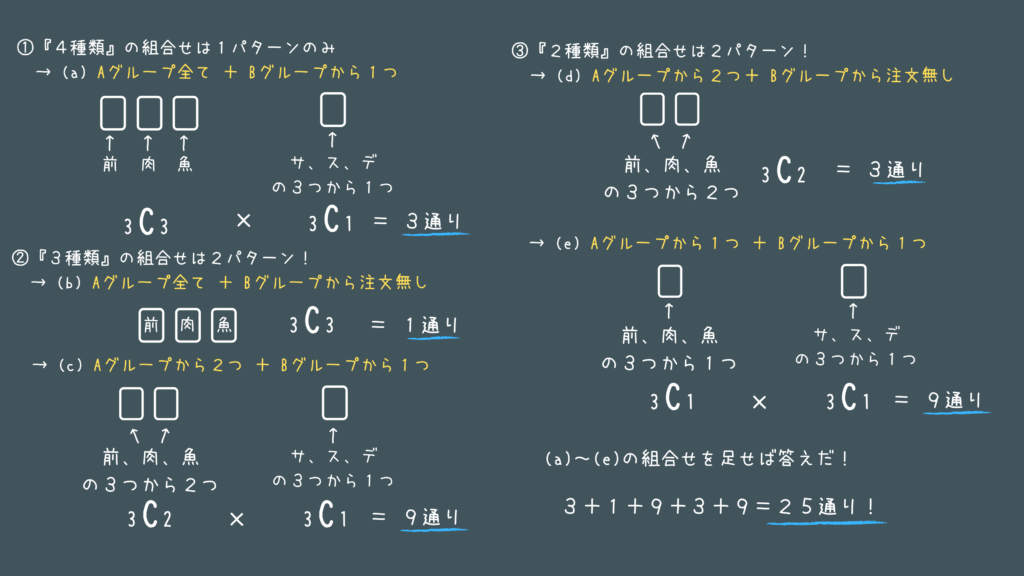
令和元年の数的の1問目です!
場合の数からの出題でしたね!
条件をきちんと整理して、ひとつひとつ丁寧に求めていけば解けちゃう問題です。
この1問は取っておきたいですね!
数的推理チャレンジ問題 No.2:「比・割合」



2問目は「比・割合」分野からの出題でしたね。
問題文も長く、条件もやや複雑ですが、丁寧に整理していけばスラっと解けちゃう問題。
落ち着いて解けば解けるのに…と本番は焦ってしまって解けなかった、という方も多そうですね!
きれいに条件を整理することが問題攻略の秘訣です。

問題文と条件がちょっとややこしいですが、整理しちゃえばこっちのもんです!
自分で整理できるようにしていきましょう。
数的推理チャレンジ問題 No.3:「整数の発展問題」


3問目は「整数」分野からの出題ですが、捨ててOKです。
興味がある人だけやりましょう!
こんな問題紹介してんじゃねぇって話ですよね(笑)
すみません。
数的推理チャレンジ問題 No.4:「扇形の面積」


4問目は扇形の面積を求める問題です!
扇形の面積の求め方はあらかじめ勉強しておかないと解けませんね!
ちょっと難しい問題ですけど、この手の問題は”三平方の定理で半径を求める”というのがお決まりのパターンです!
なのでポイントはコレです!
- OQ=半径だと気づく
- OZとZQの長さから半径を出すと気づく
これに気づかないとめちゃくちゃめんどくさいことになります。
逆にきづけばあとは簡単な計算だけ!
三平方の定理はよく出るので使えるようにしておきましょう!
数的推理チャレンジ問題 No.5:「微生物」

分野はどこになるんだろう、、5問目は「微生物の増殖」です。
文章が長すぎて難しく感じてしまう…けど、思っているほど難しくはないと思います!
きちんと整理するところが整理できていれば簡単に解けちゃいます!
- 表でまとめる
- 微生物の量に注目してみる
とくに微生物の量に注目すると、図の(MAX)の値は同じはずですから、等式で結べば簡単にa:b=1:4と求められます。
もしAの数が1からスタートしていたら、Bは4からスタートということですね!
bは6時間ごとに2倍になっていくから5回目(30時間)の時に32倍になりますね!

【数的処理の参考書】私のオススメはコレ!
やはり王道のこの2冊!
最初は理解できなくて大変だと思いますが、
どこに注目すれば問題が解けるようになるか、という部分を大事に繰り返し解いていきましょう!
ただ単に解くのではなく、
「同じようなタイプの問題がでたら、こういうところに注目して、こういう風に考えればいいんだ、こういう表でまとめればいいんだ。次は絶対自分の力で解くぞ!」
といった反省を大事にして勉強いきましょう!
解き方が決まっている問題は、繰り返し解いて解法を覚えていきましょう!
【数的推理】
【判断推理】

‘答えを丸暗記しちゃうタイプの人は要注意”です!
数的はパターンごとの解き方(考え方)を覚える科目なので!
この記事を書いた人

![公務員のライト[試験情報データベース]](https://senseikoumuin.com/wp-content/uploads/2022/12/cropped-logo-color-2.png)


















ではさっそく数的処理の問題を解いていきましょう!