「構造力学をやさしく教えていきます!」
難しくて諦めてしまう方もいれば、勉強が理解できていないまま試験に臨んで落ちてしまう人もいると思います。
でも実は公式を使うだけで解けてしまう問題ってかなり多いんですね!
勉強が進んでいる方も、そうでない方も効率よく勉強をしてもらえるように、
また、このページを見ただけで構造力学を理解していただけるように
私が重要なところをひとつひとつ”本気で”説明していきます!
長いページとなりますが、お付き合いいただけたら幸いです。
構造力学の重要度と出題頻度のページを見ながらこのページを見ていただけるとわかりやすいと思います。
ではこちらの参考書にそって説明していきますね。
![]() 土木職公務員試験 専門問題と解答 [必修科目編]
土木職公務員試験 専門問題と解答 [必修科目編]
今回は構造力学編です。
水理学と土質力学を勉強したい人はこちらをみてくださいね。
- ⇨勉強シリーズ 水理学編
- ⇨勉強シリーズ 土質力学編

教科書買ってやる気だけはあるんだけど、全然わかんねぇよ…。

徹底的に解説していくから頑張って勉強していこう!
毎年受験生からも好評の勉強ページなんだ!


【土木の専門模試スタート💡】
リリースキャンペーンということで
通常価格5000円のところ、今だけ2000円という超破格のお値段で提供させて頂きます✨
実際の問題(過去問)を見る機会も少ないと思いますので、模擬試験で本番の問題を解くことができるだけでも受ける価値はあると思います☺👍
地方上級の実際の問題(とある1年の過去問)を題材として、専門の模擬試験を実施させていただきます。
- 問題数:40問
- 時間:2時間
- レベル:地方上級(大卒程度)
問題と解説のPDFをお配りするだけでなく、動画で40問をフル解説いたします。
目次
【公務員試験の構造力学】参考書のタイトルごとの重要度

重要度はSが超大事な箇所で残りはA~Eの5段階で示してあります。
今回は重要なところは理解してもらえるように図で細かく説明し、効率が悪い問題の説明は省かせていただきます。
”重要だけどわかりずらい”
そんな問題は実際の問題を解きながら公式の使い方や、構造力学の考え方を説明していきたいと思います。
とくに理解するのが大変な「断面力図(曲げモーメント)」のところは練習問題をたくさん用意しました。
→曲げモーメントが苦手な方必見!
それでは、順番に解説していきますね。

ということで徹底的に解説していきますよ~!
【構造力学】①不静定次数

出題自体はすくないですが、この項目は土木の考え方の中心となるもので、非常に重要です。
ココの理解をおろそかにしておくと後で痛い目にあいます(笑)
支点に作用する反力 ★★★★★
支点にはたらく力は『毎回図示する』ことが大切です!
大事なところなのでわかりやすく図で説明しますね。
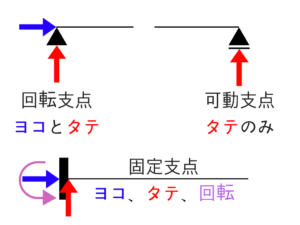
梁の問題がでたら、慣れるまではすべてこのように力を図示しておきましょう。
大きさがわからないものは、文字で置いておけばOKです!
不静定次数 ★★☆☆☆
力を図示し終わったら、その『矢印の数が反力の総数』となります!
ここは静定か不静定か判断できるようにだけしておきましょう。
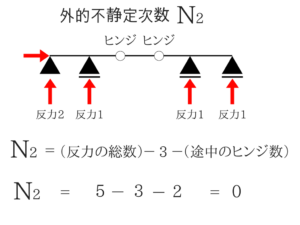
「反力の総数=矢印の数」となります。図に発生する矢印を書いていくとわかりやすいでしょう。
ちなみに0で静定となります。
【構造力学】②断面力図

断面力図からの出題が多いので、細かく説明していきます。
断面力は非常に重要です!
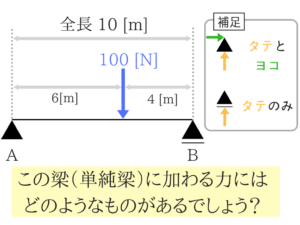
反力の求め方 ★★★★★
反力を求めるポイントは3つ
- A、B点での曲げモーメントがゼロであること
- その点に自分がいると思って考えること
- ”時計回りの力”=”反時計周りの力”です!
力のつりあいの解説はこちらを参考にしてみてください。
→物理の基礎を紹介!(教養用)
反力の公式は不静定次数の項目の「支点に作用する力」をきちんと理解していれば覚える必要はありません。
【超重要】反力は絶対に求められるように!
ただ、『反力を求める』というのはめちゃくちゃ大事なのでわかりやすく説明しますね。
慣れるまでは力はすべて図示しましょう!
まず、A点とB点に反力がはたらきますよね?
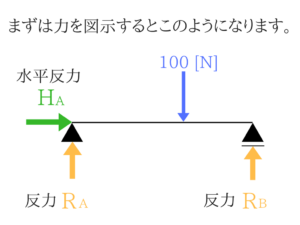
ここまで図をかくことができたら、次はタテのつり合いとヨコのつり合いをみてみます。
タテのつり合い、ヨコのつり合いを考えてみる
わからない文字はわからないままでいいので、つり合いの式をたててみましょう!

ヨコ向きの力ははたらいていませんが、きちんと図示することで土木が理解しやすくなると思います。
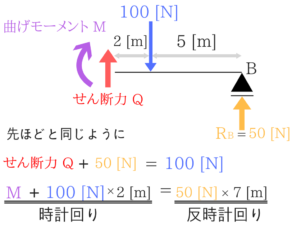
反力の大きさを求めていきます!
最後に反力の大きさを求めたいと思います。
真ん中より右側に100[N]の力があるので、なんとなくRBの方が力がたくさんかかっている気がしますよね?

でも求め方ってわかりませんよね。
回転支点・可動支点は曲げモーメントが発生しない!
めんどくさい方は公式が教科書に載っているので覚えてしまってもOKですが
これさえ理解していれば簡単に反力が求められます。

梁の問題では上の2つの支点が頻繁に出題されます。
この問題の場合でもA点とB点の「曲げモーメントはゼロ」なんですね。
時計回りの力=反時計回りの力
ということは、「時計回りに回転させる力」と「反時計回りに回転させる力」がつりあっているわけです。
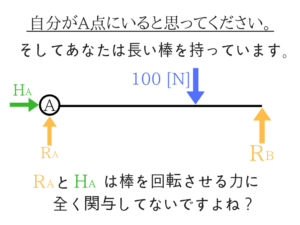
自分がA点にいて、長い棒を持っているとすると(この考え方非常に大事です)、回転させる力は100[N]とRBだけですよね?
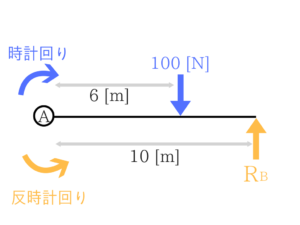
↑こんな感じです!なんとなく感覚つかめましたか?
等式で結んでみる!
そして、A点では曲げモーメントがゼロにならなければならないのでこのようになります。

RAとRBあわせて100[N]なので、RBは60[N]、RAは40[N]となりますね。
反力の求め方まとめ
単純梁などの梁での反力の求め方をまとめて紹介しておきますね!
 大事なところなので説明が長くなってしまってすいません。
大事なところなので説明が長くなってしまってすいません。
断面力の符号 ★☆☆☆☆
これはそんなに深く考える必要はありません。すぐに慣れます。
教科書に書いてある通りの意味です。
断面力の求め方 ★★★★★
曲げモーメントの大きさは、『距離×力の大きさ』で求められます。
土木の大事な考え方の一つに、切ってから考えるというものがあります。
この考え方はめちゃくちゃ大事です!
切ったところにはせん断力と曲げモーメントが作用!
そして教科書に書いてあるとおり
梁などを途中で切った場合に、曲げモーメントMXとせん断力QXが作用するということです。
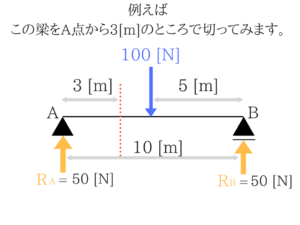 切った左側はこのようになります。
切った左側はこのようになります。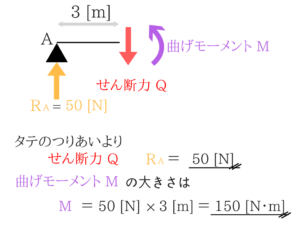
そして切った右側もこのようになります。
切ったところには曲げモーメントとせん断力が作用するということを覚えておいてください。
曲げモーメントとせん断力の関係式
曲げモーメントとせん断力の関係式は覚えなくてもいいと思いますが、一応説明しておきますね。
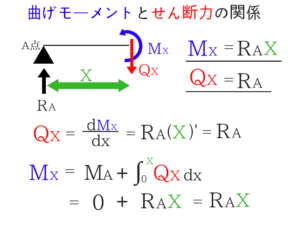
x点でのせん断力QxはMxを微分したもの、逆にMxはx=0の時の曲げモーメントにせん断力を0からx点まで積分したものを足したもの、という意味です。
⇒要は微分・積分の関係にあるわけですよね!速度と加速度の関係と同じようなものです。
ここまで見てもよくわからない方はこちらを見てみてください。

これがきちんと理解できているだけで構造力学は超簡単に見えるし、逆に理解できてないと超難しく見えると思う!

そうすればどんな形の梁でも曲げモーメント図の形がわかるんだ!

曲げモーメント図の問題がでたら切って切ってきりまくるぞ!
その都度曲げモーメントの大きさや正負を考えればいいんだね!
代表的な断面力図 ★★☆☆☆
単純梁くらいは暗記してもよいかもしれません。
それ以外は私も暗記していませんでした。

構造力学の基礎部分がきちんと理解できていれば、毎回自分で導き出すことが出来ますからね!
【構造力学】③トラスの部材力

トラスの問題は非常に多く出題されているため、しっかり説明していきますね。
とくに断面法をつかいこなせるようにしていきましょう!
トラスの部材力(1) 接点法 ★★★★☆
ヒンジの周りで切った後、わからない力は文字で置いておきましょう!
接点法とはトラスにおけるヒンジの周りで切ることで未知の力を求める方法です。
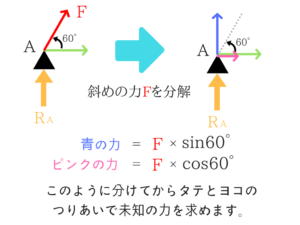 力の分解のやり方はこちらをみてください。
力の分解のやり方はこちらをみてください。
トラスの部材力(2) 断面法 ★★★★★
- まずは、支点の反力を求めます。
- そのあとに求めたい部材があるところをタテに切って考えてみましょう!
断面法とはトラスで求めたい部材力がある部材のところを縦に切ることでつり合いを計算し、その求めたい部材力を求める方法です。
トラスの問題を解いていきます!
言葉で説明してもわかりにくいので実際に問題を解いてみますね。
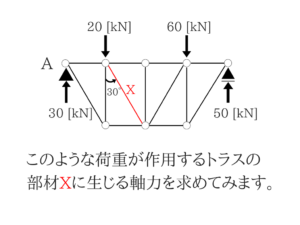 ぱっと見るととても難しそうな問題に見えますよね?
ぱっと見るととても難しそうな問題に見えますよね?
でも、実はやり方さえ知っていれば超簡単です。
断面法を使って、力をタテ・ヨコに分解!
この問題、断面法を使えば一発なんですね。
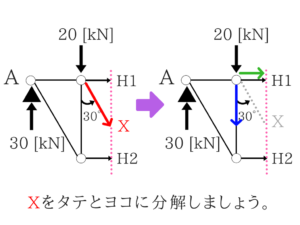
そしたらタテとヨコのつりあいの式を立てれば終わりです。
今回はヨコの力(緑)は必要ありません。

この手の問題は一回理解してしまえば、同じパターンの問題が出てきたら解くだけになるので、時間を使ってでもやり方を覚えるようにしましょう!
(3) トラスに生じる部材力の性質 ★★☆☆☆
覚えていなくても(1)の接点法や(2)の断面法を使って正負を求めればOKです!
簡単に読んでおく程度でよいと思います。
『上弦材には圧縮、下弦材には引張力が加わる』これくらいは覚えておきたいですね。

忘れちゃったり、知らなかったとしても、部材を一個一個切って考えれば、圧縮か引張かどちらか判断できるのでOKで基礎部分の理解を大事にしてください!
【構造力学】④影響線

最大曲げモーメントと最大せん断力を求める問題はそこそこ見ますが、影響線の問題は少ないと思います。

この項目を理解していなくても、公務員試験で出題される問題は、曲げモーメントの求め方やせん断力の求め方がきちんと理解できていれば、答えを導き出せる問題ばかりです。
⇒曲げモーメントとせん断力について深く理解してから勉強するべきだと思います。
今回は要点を伝えるために、実際に出題されている最大曲げモーメント、最大せん断力を求める問題を解きながら説明していきたいと思います。
着眼点 i における曲げモーメントの影響線 ★☆☆☆☆
影響線というのは、「大きさ1の単位集中荷重」が移動したときの曲げモーメントやせん断力がどのように変化するかを図示したものです。
いわば曲げモーメントやせん断力のテンプレートといったところでしょうか。

例えば、橋があったとして、車一台が端から端まで渡りきるのに、どのような影響があるのかというのが影響線があるおかげで計算できたりします。
単純梁と張出梁の影響線 ★★★☆☆
単純梁と張出梁くらいは影響線の公式として覚えておいてもいいかもしれません。
ミューラーブレスロウの定理 ★☆☆☆☆
ミューラーブレスロウの定理を使わなければ解けない問題は、基本的に国家総合職か東京都の記述の問題くらいなので飛ばしましょう。
影響線の利用 ★☆☆☆☆
単純にP=1の時の影響線がわかっているわけですからPの大きさによってそれは比例するわけです。
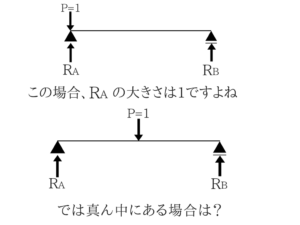
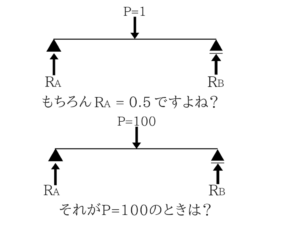
ただ比例しているってそれだけの話です。
答えはRA=50です。
間接荷重の影響線 ★☆☆☆☆
間接荷重自体、公務員試験での出題が少ないです。
飛ばしていいと思います。

一応説明しておくと、間接荷重とか関係なしに影響線をかいたあと、せん断力の影響線は間接荷重のある端から端を斜めに結び、曲げモーメントの影響線の場合は間接荷重のある所の端から端を横に結べば、それが影響線となります。(参考書の図を見てみてください)
最大せん断力と最大曲げモーメント ★★★☆☆
影響線の使い方は決まっているので解法を覚えるのが早いです。
曲げモーメントとせん断力について深く理解していれば影響線を使わなくても答えが導けます。
最近出題を見るので、実際に出題された問題を解きながら解説していきますね。
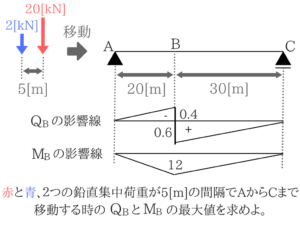

今回は問題の指示に従って【(1)影響線を使って解く解法】と【(2)強引に切って計算して求める解法】の2つを紹介していきたいと思います。
(1)影響線を使う解法
- 影響線の使い方は決まっています。
- 問題を解きながら覚えてしまいましょう!
影響線をつかいこなせるのであれば、こちらの解法の方がらくです。
まずは最大せん断力を求める!
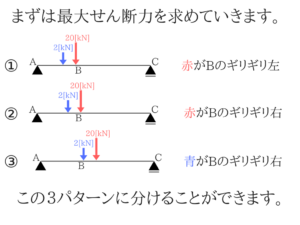
絶対値で考えるので、反対の符号を掛けるときだけマイナスをつけてください。
要は大きさだけわかればいいわけです。
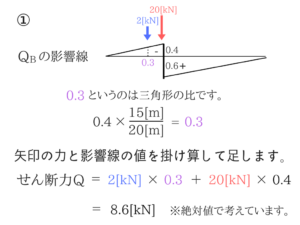
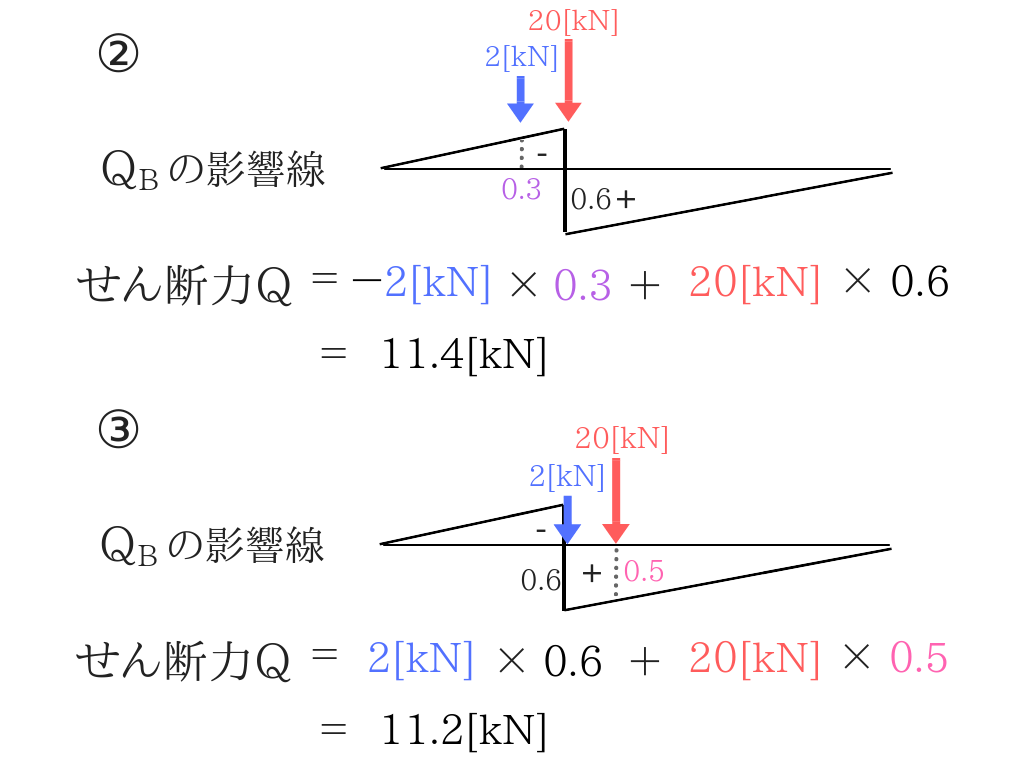
これで最大せん断力はわかりましたね。Qmax=11.4[kN]です。
同様に最大曲げモーメントを求める!
次は最大曲げモーメントを同じように求めていきます。
今回は2パターンしかありませんね。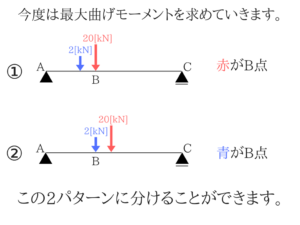
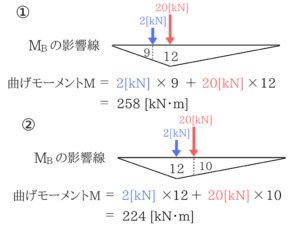
最大曲げモーメントの答えMmax=258[kN・m]ですね。
ポイントは、パターンを分けて考えることと、三角形の比で影響線の値を求めることですね。
では次に強引に切って最大値を探す方法を紹介します。
(2)切って最大値を探す解法
問題ももう一度のせておきます。
公務員の試験では、問題に従わずに自力で答えを探しだす力も大事なんですね。

5択の試験なので、どんなやり方で解いたって答えさえ見つけることができればOKです。
解法手順はこんな感じ!

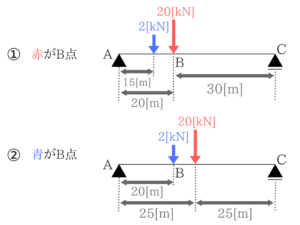
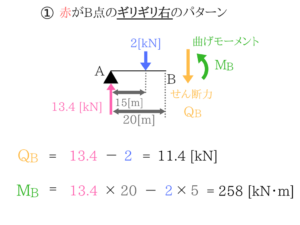
①から反力を求めていきます。
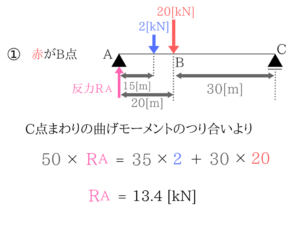
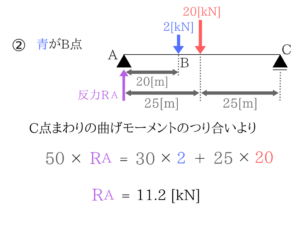 今回はA点の反力がわかればいいのでC点に自分がいると思って曲げモーメントのつりあい式を立てればOKですね。
今回はA点の反力がわかればいいのでC点に自分がいると思って曲げモーメントのつりあい式を立てればOKですね。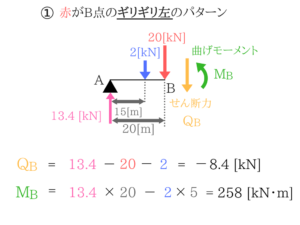
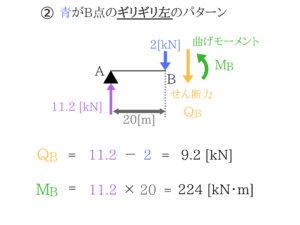
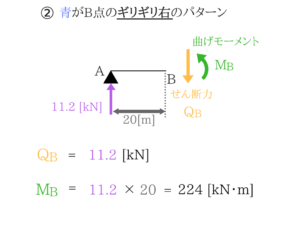
計算して出た値の中から最大のものを選べばOKです。
影響線を使わなくても、最大せん断力と最大曲げモーメントを探し出すことができちゃいましたね!
ちゃんと理解していれば、このように強引に答えを探すこともできます。


とくに曲げモーメント系の問題が切って考えるのが大事だって痛感したよ…!!
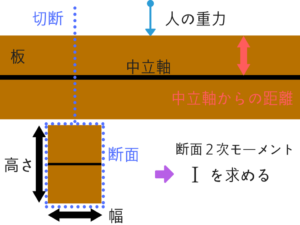
【構造力学】⑤断面2次モーメント

地方上級や国家一般職でも頻出なので断面2次モーメントはすべて理解しておきたいところです。
実際に出題されている問題は基礎的なものばかりで、この教科書に書いてあることが理解できたら確実に点がとれると思います。

非常に大事なところなので細かく解説していきたいと思います!
【断面2次モーメント】図心 ★★★★☆
- タテ方向の図心位置とヨコ方向の図心位置を求めます。
- その交点が図心となるわけですね!
- わかりにくい形の図形でも切って考えていきましょう!
図心を探せないと断面2次モーメントの問題が解けない場合があります。
図心の求め方から紹介!
この教科書だと文字ばかりで少しだけわかりずらい気がしませんか?
なので実際に図心を求めながら説明していきたいと思います。

まずは鉛直(タテ)方向の図心軸を探します!


下の長方形は「ヨコ10cm、タテ6cm」、上の長方形は「ヨコ4cm、タテ6cm」となります。
なので下の長方形は太線から3cm、上の長方形は太線から9cmとなります。

ここまで求められたらあとは計算するだけです!

図心は太線から33/7(約4.7)cmのところにあることがわかります。

次は水平(ヨコ)方向の図心軸を探します!
次はヨコ方向の図心の位置を求めます。
先ほどと同じ手順で太線を下の図のようにした場合で計算すればOKです。
右の長方形は太線から2cm、左の正方形は太線から7cmですね。
そして面積は、右の長方形は12×4で48cm2、左の長方形は6×6で36cm2となりますよね。
 同じように計算してみます。
同じように計算してみます。 ヨコ方向は太線から29/7(約4.1)cmのラインに図心があることがわかります。
ヨコ方向は太線から29/7(約4.1)cmのラインに図心があることがわかります。
タテの図心軸×ヨコの図心軸⇒交点が図心!
タテ方向の図心のラインとあわせてみます。
このようにして図心を求めることができます。
初めてやると難しいかもしれませんが、慣れてしまうと作業のような感じになってくると思います。
断面2次モーメント ★★★★★
- 公式の使い方を覚えるのが一番早いです。
- 公式の文字が図形のどこを表しているのかきちんと覚えましょう!
断面2次モーメントを求めよ、という問題は頻出なので、詳しく説明していきたいと思います。
断面2次モーメントの公式は絶対に覚えて!
 これだけ覚えておけばいいのですが、大事なのは使い方…ということで、今からその使い方を紹介していきたいと思います。
これだけ覚えておけばいいのですが、大事なのは使い方…ということで、今からその使い方を紹介していきたいと思います。
nx=図心軸!⇒断面2次モーメントは最小に!
まずは補足説明からしますね。
図心軸に関する断面2次モーメントの公式も覚えておこう!
とりあえず図心軸に関する断面2次モーメントの公式も暗記しておいてください。
断面2次モーメントの公式の使い方
では実際に断面2次モーメントを求めてみましょう。
公式である『 Ix=Inx+Ay2』に当てはめて計算したいところですよね。
面積(A)と図心までの距離(y)を求める!
そこで、まずは面積と図心までの距離を求めてみたいと思います。
後はこれを公式に当てはめて計算するだけです。


なんとなく雰囲気つかめましたか?
ここもやり方さえ覚えてしまえば、あとは同じ作業の繰り返しです。
断面2次モーメントは重要なので、きっちり理解できるように勉強しましょう!
簡単な図形の図心軸に関する断面2次モーメント ★★★★★
- 長方形と三角形は公式として確実に覚えておきましょう!
- この後の分野でも非常に多く使用します。
とくに長方形、三角形の断面2次モーメントは超頻出です!
暗記して確実に使いこなせるようにしましょう!

この公式は構造力学だけでなく土木として非常に大事です。
何度も書いて絶対に暗記してくださいね!

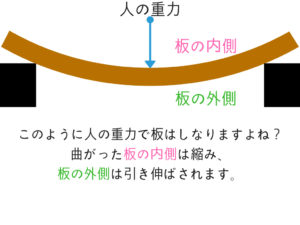
【構造力学】⑥ひずみと応力度

大事なところなんですけど理解するのが大変なんですね。
でも地方上級や国家一般職に出題される問題は基礎的なものばかりです。
理解できるように、問題を解きながらわかりやすく解説していきたいと思います。
軸応力度σと軸ひずみεの関係 ★★★★★
- 結局は『解法を覚える』ということになります。
- 解法か決まっているので、何回も書いて覚えてしまいましょう!

難しい分野ではありますが、結局は解法を覚えるだけです。
応力度の公式は絶対に覚えて下さい!
この公式はめちゃくちゃ大事です。
覚えてもらいたい公式を書くので、絶対にメモしてくださいね。

実は応力度の式とフックの法則は同じ意味!
この公式を変形したものと、ばねの公式を覚えておくと便利です。
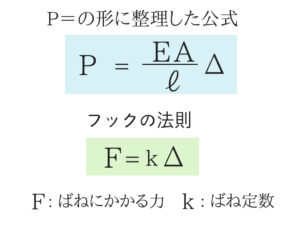
実は棒材などの問題は、ばねと置き換えて考えることができるんですね!
k=EA/ℓ とすると、応力度の公式とフックの法則は同じ形となります。
実際に国家一般職で出題された棒材の問題を2パターンの解法で解いてみます!
棒材の解法(1) 普通の解き方
普通に解くポイントは2つです。
- 棒を切って考え、値を公式に代入すること
- 結局、伸び量はゼロであるということです!
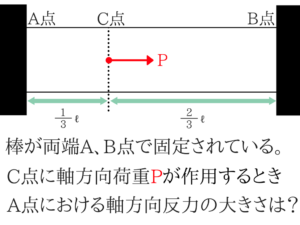
(※棒の重さは無視できるものとします。また断面積も等しいものとします。)
では、この問題を(1)普通の解法で解いてみますね。
はたらく力を図示する!
まずははたらく力を図示します。
曲げモーメントとタテ方向の力は作用しませんね。
ヨコ方向の力のみが作用します。
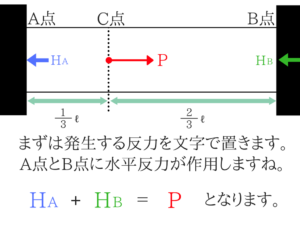
最終的にHAを求めるということですね。
切って考える!
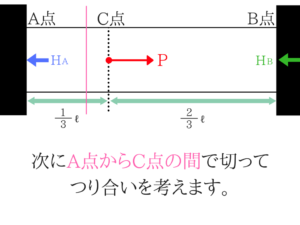
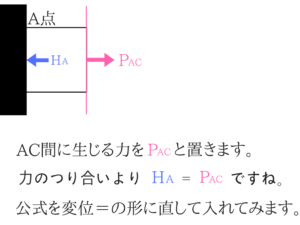
応力度の公式をΔ=に変形!
先ほどの公式を「変位(棒材の伸び)=」の形に直します。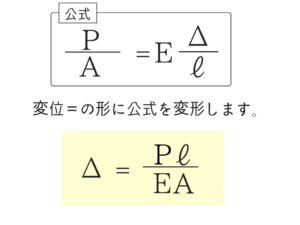
まずはAC間の伸び(変位量)を求める!
そして、値を代入してAC間の伸びを求めておきます。
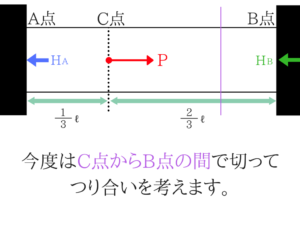
同様にCB間の伸び(変位量)も求める!
先ほどと同じように今度は、CB間で切ってCB間の伸びを求めていきましょう。
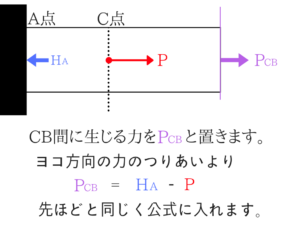

両端が固定されている⇒変化量はゼロ!
ここでポイントとなるのが、「両端が固定されている」ということです。
どういうことだと思いますか?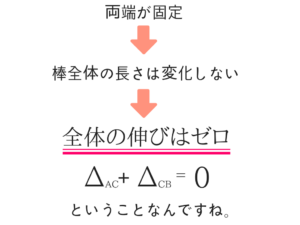
固定(静止)されているわけですから、変化量はゼロになります。
後は計算するだけ
代入して実際に計算してみますね。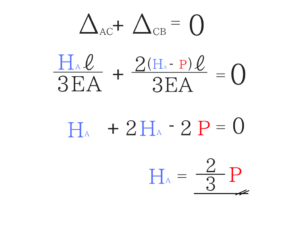 HAをこのように求めることができるんですね。
HAをこのように求めることができるんですね。
ちなみにHA+HB=Pなので、HBは1/3Pとなります。
ではもう一方の解法を紹介していきます。
棒材の解法(2) ばねとして考える解き方
- ばね定数k = EA/ℓ のばねとして考えるということです。
- 力の大きさはばね定数に比例します!
先ほど説明したフックの法則を使います。
慣れてしまうと、こちらのやり方のほうが簡単です。
もう一度応力度の公式から紹介!
公式をもう一度画像で確認してみますね。

フックの法則のばね定数というのは、簡単にいうとばねの伸びやすさのことなんですね。
⇒変化量(伸び量)はばね定数の大きさに比例します。
応力度の公式とフックの法則の関係
そしてこの2つの公式、形が似てませんか?
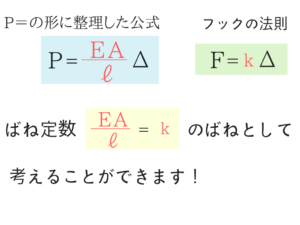
棒材⇒ばねとして考えることができる!
実はPは力Fも力、Δはどちらも変化量(伸び量)ですから、このような棒材はばねとして考えることもできるんですね。
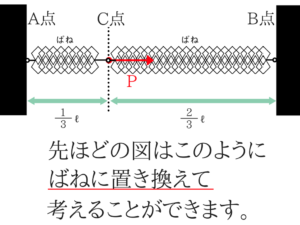
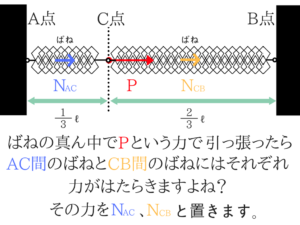
少しわかりずらいとは思いますが、ばねにかかる力というのはばね定数に比例するんですね。
ばね定数が大きいとばねが伸びにくくなり、小さいとばねが伸びやすくなります。
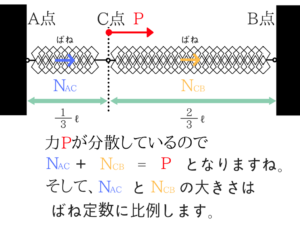
なのでこの関係を式で表してみます。


ここまでくればもう答えはわかるかもしれませんが、一応きちんと計算しておきます。
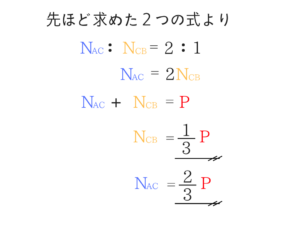
この力が棒ACを通して壁に伝わっているのでAの支点反力も2/3Pとなります。

とりあえず2つの解法を説明しましたが、基本的には最初に説明した解法をマスターしてくださいね。
ひずみの解法
- 難しく見えますが、解法が決まってます。
- 知識問題として解き方を覚えてしまいましょう!
長くなってしまいますがひずみの方も問題を解きながら解説していきたいと思います。
応力度の公式!
使用する公式は応力度の公式です。
ひずみの問題を解いてみよう!
理解するのが難しい分野となりますので、実際に出題された問題を解きながら解説していきますね。
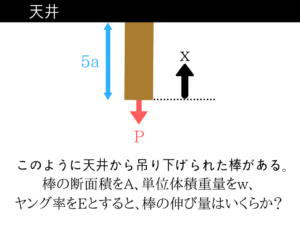
xで切って、つり合いの式!
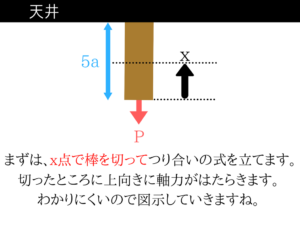
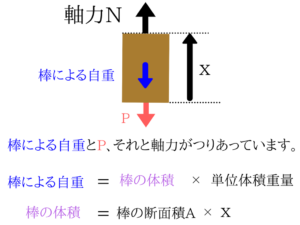
単位体積重量に体積をかければ、重力となります。
重力はAxw
棒の体積はAxなので、重力はAxwとなりますね。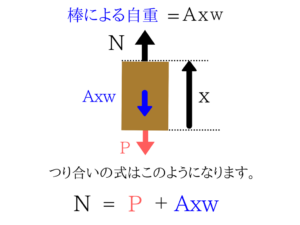
ここで一旦おいておきます。
微笑要素dxの伸び量をΔdxとして考える


Δdx/dxというのは微小単位で考えたときの軸ひずみのことなので、
実際の変位Δというのは、この式を0~5aまで積分したものとなります。
後は積分するだけ!
ここまでできたら、あとは計算するだけです。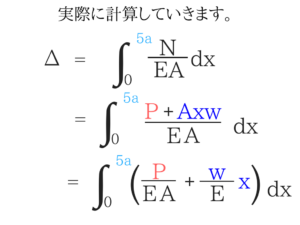
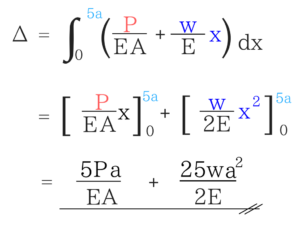
めちゃくちゃ難しく感じますが、一度解法や考え方をマスターしちゃえば、実際の問題はスラスラ解けちゃうと思います。
出題される問題がこのパターンしかないので、今回の問題で流れをマスターしておきましょう!

積分のやり方がわからない方はこちらを見てみてください。
→数学の基礎を紹介!
温度変化による伸び ★★☆☆☆
これは公式だけとりあえず覚えておいてください。
試験での出題は少ないです。
(国家総合職等の試験を受ける方はやっておこう)
鉄筋コンクリート柱の軸応力度 ★★☆☆☆
ここも教科書に書いてある通りに理解してください。
試験での出題も少ないです。
曲げ応力度 ★★★☆☆
これは国家総合職や東京都などの記述問題での出題が多いです。
短い柱と長い柱のところで、この知識が必要なので一応説明しますね。

そして、発生する曲げモーメントから曲げ応力度を算出します。

この項目は1.8 短い柱と長い柱のところで詳しく説明するので、今はこれだけ覚えておいてください。
断面係数と縁端応力度 ★★★☆☆
- 断面2次モーメントは『変化している方向が高さ』になります。
- 今回の図の場合、下向きに変化しているので板の厚さが高さとなります。
断面二次モーメント÷縁端距離⇒断面係数
単純に断面係数は「断面2次モーメント ÷ 縁端距離」ということです。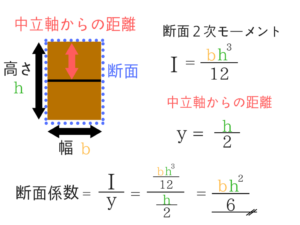
先ほどの図で説明するとこのようになります。
断面係数を求めよ、という問題が出たらこのように計算してくださいね。
せん断応力度τ ★☆☆☆☆
簡単に読んでおく程度でよいでしょう。
出題も少ないです。
せん断応力度τとせん断ひずみγの関係 ★☆☆☆☆
この分野の問題は総合職の記述などで出題されています。
飛ばしてOKだと思います。
モールの応力円 ★★★☆☆
- 座標が求められるようになる程度でOKです!
- y軸はせん断力、x軸は曲げ応力度を表しています。
この説明のページ、見ただけで頭が痛くなりますよね…。
本気で全部理解しようと思ったら一カ月くらい勉強しなきゃいけない気がします。

ただ、公務員試験で出題される問題は基礎だけですから、基礎部分だけは理解しておいてほしいなと思います。
モールの応力円は基礎部分だけ理解しておこう!
モールの応力円自体は出題が少ないですが、せん断系の分野なので土を切ったりする土質力学で出題されます。
土質力学の方でも説明しますが、こちらでも基礎の部分だけ簡単に説明しておきますね。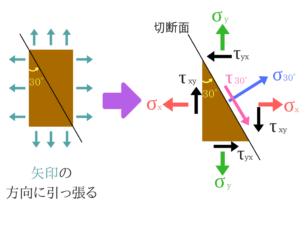 板や土などをせん断した場合このように力が働きます。
板や土などをせん断した場合このように力が働きます。
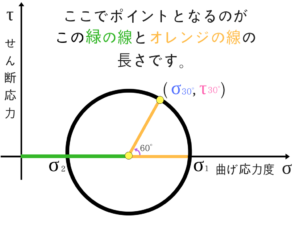
求めるのはσ30°とτ30°です。
モールの応力円の使い方を紹介①
そしてモールの応力円を描きます。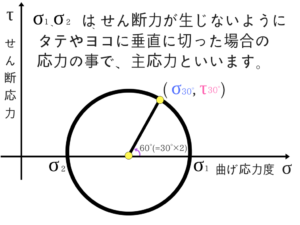 角度(60°)のところは公式で2θなので30°の場合は30°×2で60°となります。
角度(60°)のところは公式で2θなので30°の場合は30°×2で60°となります。
ここまで描けてしまえば、あとは座標を求めるだけとなります。
モールの応力円の使い方を紹介②
では、どうやって座標を求めるのか説明しますね。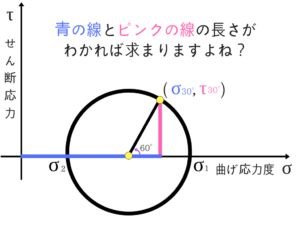

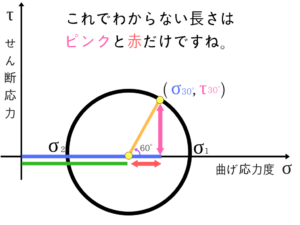
 ごちゃごちゃするので、値は書きませんがこのようになります。
ごちゃごちゃするので、値は書きませんがこのようになります。
これがモールの応力円の基礎なのでこれくらいは理解できるようにしたいですね。

長さ成分の分解がわからない方はこちらをみてみてください。
→物理の基礎を紹介!
モールの応力円について、どうしても理解したいという方はこちらの都庁の例題を参考にしてみて下さい!
→東京都庁1類B平成28年度土木問3(2)
(難しいので飛ばしてOKです)
重要度が高いところから重点的に勉強していきましょう!
モールの応力円が理解できてなくても他を頑張れば余裕で試験に受かります。

「応力度とひずみ」、「曲げ応力度」、「断面係数」を今勉強しているところ!
【構造力学】⑦構造物の変位

この分野は非常に難しいですが、覚えるところや勉強しなければいけないところは限られています。
とくに梁のたわみを求める式は非常に重要です。
では公式の使い方や考え方を細かく説明していきますね。
たわみとたわみ角 ★★★★☆
dy/dx = たわみ角 と覚えておきましょう!
たわみ角はyの式をxで微分すれば求めることができるということです。
たわみをxで微分⇒たわみ角!

数学の基礎がわからない方はこちらを見てみてください!
→数学の基礎を紹介!
微分方程式による解法 ★★★☆☆
- 公式を1回積分したものがたわみ角、2回積分したものがたわみとなります。
- 境界条件もきちんと考慮することを忘れないようにしましょう!
ここは理解するのが難しい分野です。
基礎的な問題だけできればOKなのでとりあえず公式は覚えてください。

国家一般職と地方上級を希望する方はたわみの公式だけきちんと覚えられれば、最悪微分方程式は理解してなくても問題無いとは思います。
発展した問題は国家総合職の記述式の試験で多く出題されています。
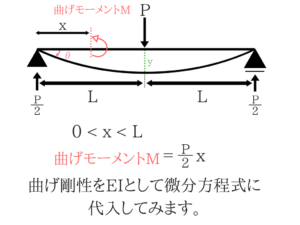
微分方程式の使い方・考え方
一応細かく説明していきたいと思います。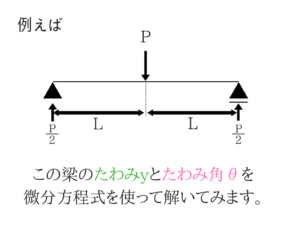
たわみ角(ピンク)とたわみ(緑)を求める!
下の図のピンクのθがたわみ角、緑のyがたわみでこれを求めていきます。
微分方程式の公式はコレ!
dy/dx⇒たわみ角、yがたわみです!
 微分方程式は、ーMx/EI(右辺)を積分して求めたいものを求めるんですね。
微分方程式は、ーMx/EI(右辺)を積分して求めたいものを求めるんですね。
曲げモーメントを代入!

積分するとこのようになりますよね。
そしてこの問題をとくポイントは境界条件をきちんと考慮することなんです。
境界条件とは何か?
では境界条件ってなんなんでしょうか。
今からそれを説明します。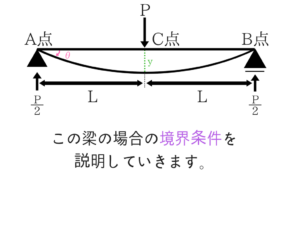
境界条件はコレ!
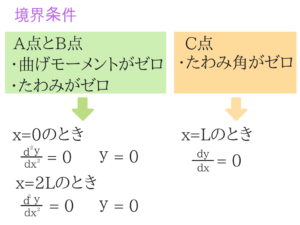
この境界条件と微分方程式から、たわみとたわみ角の値を算出していきます。
境界条件と微分方程式からたわみとたわみ角を求める!
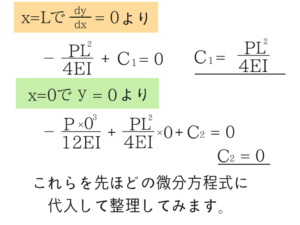


これでたわみとたわみ角を求めることができました。
まぁこれは少し難しいと思います。
東京都や国家総合職を希望する方は使いこなせなければなりませんが、たわみの式は公式として暗記できるので、これらのやり方はできなくても市役所や国家一般職の試験においては大丈夫です。
たわみの公式はこの章の最後の項目の「梁のたわみを求める式」のところにのっているので、確実に暗記するようにしてください。


弾性荷重法 ★★★☆☆
解法が決まっているので、覚えてしまいましょう!
最終的にB’点のギリギリ手前で切ったところの
- 曲げモーメントがたわみ
- せん断力がたわみ角
となります。
これもたわみとたわみ角を求める方法の一つで、片持梁などで使用します。
弾性荷重法でたわみとたわみ角を求める!
こちらも実際に説明していきます。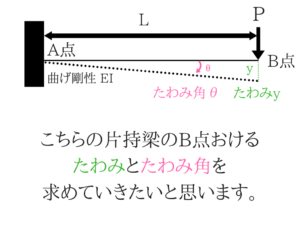
まずはB⇒Aにかけての曲げモーメントを求める!
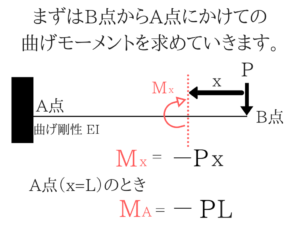
曲げモーメントは適当な箇所で切って、その都度計算して調べればどんな構造物の曲げモーメント図も書けます。
⇒このような癖をつけると曲げモーメント図の問題が出た時に確実に解けるようになります。
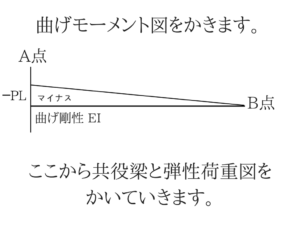
次は曲げモーメント図をかく!
共役梁と弾性荷重図をかく!
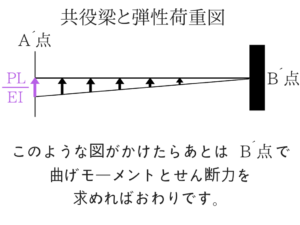
この図がかけるのがポイントです。
なんでこんな図になるのかと思うかもしれませんが、この形(流れ)を覚えてください。
かけてしまえば簡単にたわみ角とたわみを求めることができます。
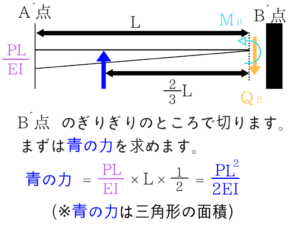
青の力は三角形の部分の面積となり、B’点から2/3Lのところに作用します。
わからない方は1.2 断面力図 反力の求め方のところを参照してください。
B’での曲げモーメントがたわみ!せん断力がたわみ角!

B’点での曲げモーメントがたわみ、せん断力がたわみ角となるんですね!
弾性荷重法というのは理解するよりも、解法が決まっているので覚えるといった感じです。
やり方さえ覚えてしまえば、実際の問題もすぐにできるようになると思います。
エネルギー法 ★★☆☆☆

エネルギー法は地方上級や国家一般職を希望するのであれば飛ばしていいレベルだと思います。
単位荷重法だけは、試験での出題が多いのでここだけ詳しく解説したいと思います。
単位荷重法 ★★★★☆
- 断公式の上線つきのMは、P=1を作用させたときの曲げモーメント
- 上線つきのNはP=1を作用させたときの軸力となります。
公式は参考書にのっているものを覚えてください。
とはいってもこの公式、どうやって使うか全然わかりませんよね。
単位荷重法を使う問題を解く!
なので使い方を覚えてもらうために実際に出題されている問題を単位荷重法を使って解いていきます。
トラスでの出題が多くみられるので、トラスの問題を解いていきます。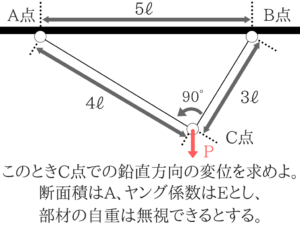
接点法を使ってトラスの軸力を求める!
実際に解いていきますね!
まずはトラスの軸力を求めていきます。
トラスなので接点法を使えばすぐに求められます。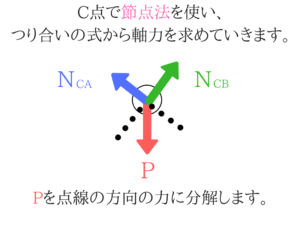
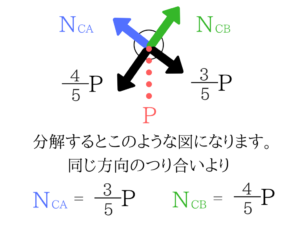
3:4:5の三角形なので、これに気づくことができるとすぐに求められますね。
もちろん角度をθとおいて力を分解すればOKです。
単位荷重法の公式を使う!
あとは公式に当てはめるだけですね。
上の線がついているものはP=1としたときの軸力となります。
値を代入していけば終わりですね。


この問題のポイントは’’単位荷重法を使うということに気づく’’ことです。
使い方はあらかじめ勉強しておかなければなりませんが、これに気づくだけで一気に簡単な問題となってしまいます。
マトリックスを用いる方法 ★☆☆☆☆
国家総合職でしか出題を見たことがありません。飛ばしましょう。
梁のたわみを求める式 ★★★★★
問題を解くためには公式を覚えるだけでなく、使い方をマスターしましょう!
梁のたわみを求める式はクソ大事!
梁のたわみを求める式は絶対に覚えてください!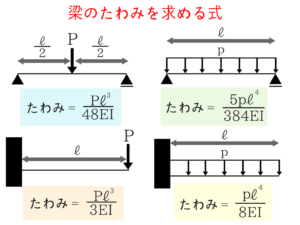
ここまでの微分方程式やエネルギー法などを理解していなくても、この式さえ覚えていれば解ける問題が非常に多く出題されています。
梁のたわみを求める式を使う問題を解く!
今回はその使い方と解法を、実際の問題を解きながら解説していきますね。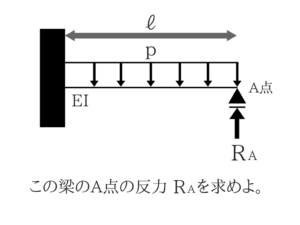
この問題は梁のたわみを求める式だけで解くことができます。
分解して考えてみることが大切!
この梁を下の図のように考えてください。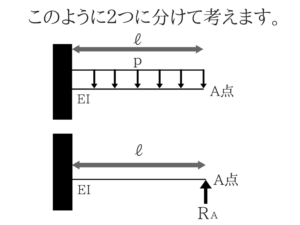
A点でのたわみの公式は覚えてますか?
梁のたわみを求める式は絶対覚えておいてくださいね。
「A点でのたわみは等しい」がポイント!
そしてポイントなのが「A点でのたわみは等しい」ということです。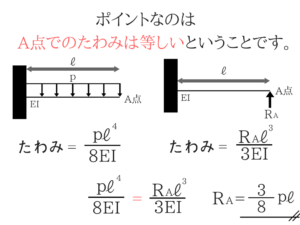
これで終わりです。簡単ですよね?
このようにたわみの問題は梁のたわみを求める式だけで解けてしまう問題が頻出しているので、公式の使い方は絶対にマスターするように!!
ここまで読んでもうまく理解できない方はこちらもチェックしてみてください!
→【たわみの求め方】例題をたくさん解く!

ネコ君も絶対に使い方をマスターするように!

【構造力学】⑧短い柱と長い柱

とくに長い柱での座屈でオイラーの公式を使用した問題が頻出しています。
この分野はそんなに難しくないうえ、点数につながるので頑張って勉強していきましょう!
短い柱に作用する応力度 ★★★★☆
この公式だけ覚えて使えるようにしましょう。

使い方は難しくありません。教科書の問題を解いて練習しましょう。
ちなみに図心軸に関する円の断面2次モーメントはπ(直径)4/64です。
長い柱での座屈 ★★★★☆
- オイラーの座屈荷重の公式は絶対に覚えてください。
- 有効長さ係数も確実に覚えてください。

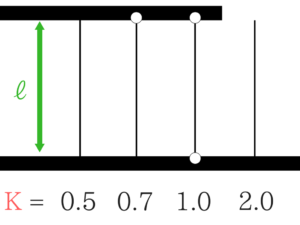
これを覚えるだけで問題が解けます!
実際に出題も多いですので、絶対覚えてくださいね。


【構造力学】⑨弾塑性と塑性ヒンジ

この分野は国家一般職、地方上級を希望するかたは勉強しなくてもよいでしょう。飛ばしてOKです。
国家総合職の記述試験ではめちゃくちゃ出題されますが、国家一般職や地方上級の試験では出題されないでしょう。
出題されたとしてもほとんどの人ができないと思うので大丈夫です。



長々とお疲れさまでした!
【他の受験生は↓の記事を見て効率よく対策しています!】

私が珍しく本気で解説しているから、上の記事はぜひチェックしてくれ!
ココまで勉強したら過去問に挑戦するのもアリです!
実際に出題されている問題を解説しています↓
![公務員のライト[試験情報データベース]](https://senseikoumuin.com/wp-content/uploads/2022/12/cropped-logo-color-2.png)
















