【曲げモーメントの求め方】「難しい」「苦手」だと決めたのはキミじゃないのかい？

曲げモーメントって意味不明！
嫌い！苦手！見たくもない！

そう思っている人のために、私が曲げモーメントの考え方や実際の問題の解法を紹介していきたいと思います。

曲げモーメントって理解するのがすごい難しいくせに重要なんです…
もう嫌になりますよね…!!

誰もが土木を勉強しようと思っていて
はじめにつまづいてしまうポイントだと思います。

でも実は、そんな難しい曲げモーメントの勉強も
”誰かに教えてもらえれば簡単”なんですね。

私も実際に一人で勉強して、理解できてなくて、と効率の悪い勉強をしてしまいました。
一生懸命勉強して公務員に合格できた私の知識を参考にしていただけたら幸いです。

では「曲げモーメントに関する基礎知識」と「過去に地方上級や国家一般職で出題された良問を6問」をさっそく紹介していきますね！

土木を勉強していて最初につまづくのが曲げモーメントです！
実際に出題されている問題は基本的な知識さえあれば解けるので、これから紹介するポイントはきちんとおさえておくようにしましょう(^o^)/

公務員試験に特化した専門土木速習講座がスタートしました！
土木の専門科目は誰かに教えてもらうと超簡単に見えると思いますので、興味がある方はチェックしてみて下さい☺

土木の速習講座のパンフレット&★過去の頻出テーマはこちらになります❕❕

【曲げモーメントに関する基礎知識】

まずは曲げモーメントに関する基礎知識から説明していきます。

文章で書いても理解しにくいと思うので、とりあえず重要な点だけまとめて紹介します。

曲げモーメントの重要な基礎知識

このポイントを理解しているだけで曲げモーメントを使って力の大きさを求める問題はすべて解けます！

曲げモーメントに関する知識・考え方で重要なところはアンダーラインを引っ張っておきますね！

曲げモーメントの演習問題6問解いていきます！

解いていく問題はこちらです。

覚えることはこれだけでOKです。
とくに”反力を求めよ”という問題は超頻出です！
ポイントをきちんと理解していれば問題がスラスラ解けちゃうからしっかりこの記事の説明をよく見ておきましょう！

曲げモーメントの計算：①「単純梁の反力を求める問題」

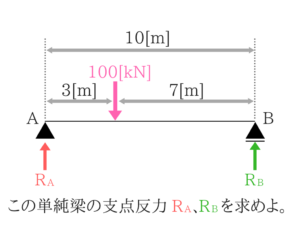まずは基礎となる単純梁の支点反力を求める問題から解いていきます。
ぱっと見ただけでも答えがわかりそうですが、曲げモーメントの知識を使って解いていきます。

反力を求めるというのは土木の問題での基礎となるので、きちんと求められるようにしましょう！

①可動支点・回転支点では、(曲げ)モーメントはゼロ！

この問題を解くために必要な知識は、可動・回転支点では(曲げ)モーメントがゼロになるということです。

A点とB点で曲げモーメントはゼロという式を立てれば答えが求まります。
実際に計算してみますね！

回転させる力は「力×距離」⇒梁は静止している

このように、可動・回転支点では(曲げ)モーメントがゼロになるという考え方(式)はめちゃめちゃたくさん使います。
簡単ですよね！

鉛直方向のつり合いの式を使ってもOK

もちろん、片方の支点反力だけ求めてタテのつりあいから「R_A＋R_B＝100kN」に代入しても構いません。
慣れるまでは毎回、モーメントのつり合いの式を立てて、反力を求めていきましょう。

単純梁の反力を求める問題のアドバイス

詳しい解説はこちら↓
▼力のモーメント！回転させる力について

支点の反力を求めるのは、構造力学の一番基礎の部分！
梁の問題を解くときにまず最初にやらなきゃならないことだから絶対に覚えるようにしましょう！

曲げモーメントの計算：②「分布荷重が作用する場合の反力を求める問題」

分布荷重が作用する梁での反力を求める問題もよく出題されます。
考え方はきちんと理解していなければいけません。

②分布荷重が作用する梁の反力を求めよう！

では基礎的な問題を解いていきたいと思います。今回は三角形分布する場合の問題です。
最初に分布荷重の問題を見てもどうしていいのか全然わかりませんよね。

でもこの問題もポイントをきちんと抑えていれば簡単なんです。
実際に解いていきますね！

合力は分布荷重の面積！⇒合力は重心に作用！

三角形の重心は底辺(ピンク)から1/3の高さの位置にありますよね！

図示してみよう！

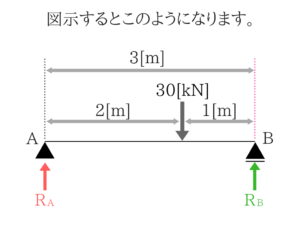
ここまで図示できたら、あとは先ほど紹介した①の単純梁の問題と要領は同じですよね！

可動支点・回転支点では、曲げモーメントはゼロ！

モーメントのつり合いより、反力はすぐに求まります。
可動・回転支点では、曲げモーメントはゼロですからね！

なれるまでに時間がかかると思いますが、解法はひとつひとつ丁寧に覚えていきましょう！

分布荷重が作用する梁の問題のアドバイス

机の上にスマートフォン(長方形)を置いたら、四角形の場合は辺から1/2の位置に重心があるので、スマートフォンの重さは画面の真ん中部分に作用しますよね！
⇒これを鉛筆ようなものに変換できるわけではありません、ただ重心に力が作用しているというだけです。(※スマートフォンは長方形でどの断面も重さ等が均一&スマートフォンは3次元なので、奥行きは無しと仮定した場合)

分布荷重は慣れるのが大変です。理解しちゃえば簡単なんですけどね。

曲げモーメントの計算：③「ヒンジがある梁（ゲルバー梁）の反力を求める問題」

ヒンジがついている梁の問題は非常に多く出題されています。
これもポイントさえきちんと理解していれば超簡単です。

③ヒンジがある梁（ゲルバー梁）の反力を求めよう！

実際に市役所で出題された問題を解いていきますね！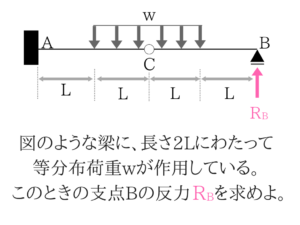

ヒンジ点で分けて考えることができる！

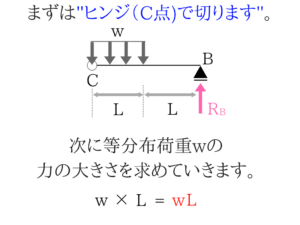
まずは上記の図のようにヒンジ点で切って考えることが大切です。
ただ、分布荷重の扱い方には注意が必要です。

分布荷重は切ってから重心を探る！

今回の問題には書いてありませんが、分布荷重は基本的に単位長さ当たりの力を表しています。
例えばw[kN/m]などで、この場合は「1mあたりw[kN]の力が加わるよ～」ということですね！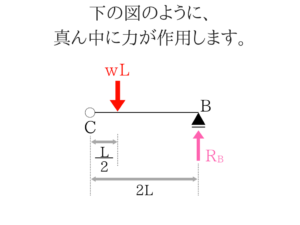

先ほどのスマートフォンの例でいうと、スマートフォンを真っ二つに切って、右半分の力のつり合いを考えていくということですね(笑)
スマートフォンは半分になったので、また辺から1/2の位置に力が作用します！
(スマートフォンは3次元なので、奥行きは無しと仮定)

ヒンジ点では曲げモーメントはゼロ！

要はヒンジ点では回転させる力は働いていないので、回転させる力のつり合いの合計がゼロになります。

ヒンジがある梁（ゲルバー梁）のアドバイス

ヒンジ点では曲げモーメントはゼロですからね！
そこからつり合いの式が立てられるから絶対に覚えておきましょう！

曲げモーメントの計算：④「ラーメン構造の梁の反力を求める問題」

ラーメン構造の梁の問題もよく出題されます。
これもポイントをきちんと理解していれば普通の梁の問題と大差ありません。

④ラーメン構造の梁の反力を求めよう！

では実際に出題された基礎的な問題を解いていきたいと思います。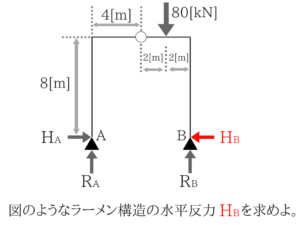

HBを求める問題ですが、いくら基礎的な問題とはいえ、はじめて見るとわけわからないですよね…。

回転支点は曲げモーメントはゼロ！

回転支点(A点)では、曲げモーメントはゼロなので、RBの大きさはすぐに求まりますよね！

回転させる力は「力×距離」です。
A点まわりについて考えてみると、A点というのは、HAやHBなどの水平反力の作用線の延長線上にありますよね！
⇒ということは回転させる力は働かない(距離＝0)ということになります！

ヒンジ点で切って考える！

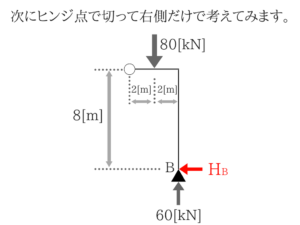
この図が描けたらもうあとは計算するだけですね！

ヒンジ点では曲げモーメントはゼロ

回転させる力はつり合っているわけですから、「時計回りの力＝反時計回りの力」で簡単に答えは求まりますね！

ラーメン構造の梁のアドバイス

ちなみに、ヒンジ点で切って右側だけ考えましたが、鉛直方向のつり合いより、ヒンジ点には上向きに20[kN]の鉛直反力が加わっていることになります。

そこで、ヒンジ点で切った左側の図について考えてみたとき、作用反作用の法則より、ヒンジ点には下向きに20[kN]の鉛直反力が加わっていることになります。
まぁヒンジ点より左側の図はRAが20[kN]で、それ以外に鉛直方向の力は無いですから、ヒンジ点に下向きの力が同じ大きさだけ加わっているのはすぐにわかりますよね！

この関係は水平方向についても同じです。

曲げモーメントの計算：⑤「曲げモーメントが作用している梁の問題」

曲げモーメント自体が作用している梁の問題も結構出題されています。

作用している曲げモーメントの考え方を知らないと手が出なくなってしまうので、実際に出題された基礎的な問題を一問解いていきます。

⑤曲げモーメントが作用している梁のせん断力と曲げモーメントを求めよう！

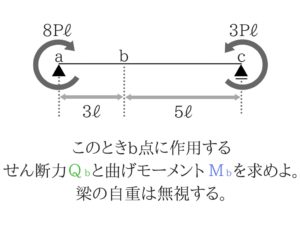これは曲げモーメントとせん断力を求める基本的な問題ですね。
基礎がきちんと理解できているのであれば非常に簡単な問題となります。
わからない人はこの問題を復習して覚えてしまいましょう！

曲げモーメントが作用している梁のポイント

では解いていきます！

曲げモーメントの単位は、例えば[kN・m]等です。
今までずっと回転させる力は「力×距離」だと言ってきましたよね！
単位の部分を意識してみるとうまく理解できるかもしれません。

時計回りの力＝反時計回りの力

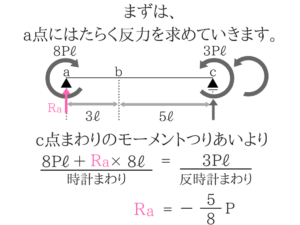とりあえずa点での反力を上向きにおいて計算しました。
これは適当に文字でおいておけばOKです！

計算してみて、プラスなら上向き、マイナスなら下向きということになります！

力を図示(反力の向きに注意)

計算した結果、符号がマイナスだったので反力は上向きではなく下向きということがわかりました。

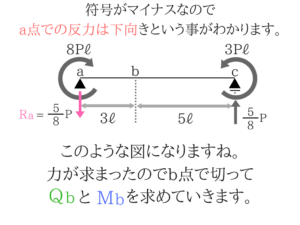
b点で切って考えてみる

b点にはせん断力と曲げモーメントが作用しています。

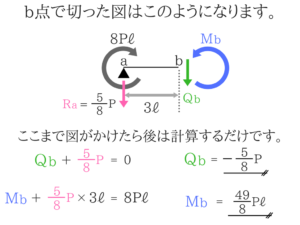Mbを求めるときも「時計回りの力」＝「反時計回りの力」で計算しています。
Qbは鉛直方向のつり合いだけで求まります。

曲げモーメントが作用している梁のアドバイス

曲げモーメントの計算：「曲げモーメント図の問題」

土木の教科書に載っている曲げモーメント図の問題を解いていきたいと思います。
曲げモーメント図の概形を選ぶ問題は頻出です。

【まずコメント】
最初は難しいと感じるかもしれないですが、公務員試験に出る曲げモーメント図の問題は基礎的なものばかりなので、解法・考え方を覚えてしまえば簡単に解けてしまう問題ばかりです！
⇒基礎部分の理解は大事にしていきましょう！

⑥曲げモーメント図の問題を解こう！

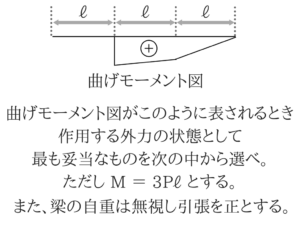
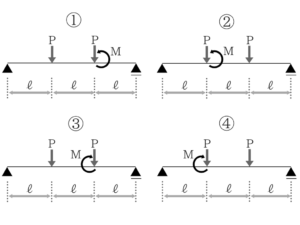曲げモーメント図が書いてあってそれを選ぶ問題の場合、選択肢を利用するのがいいと思います。

選択肢をチェックしていく問題なので、①～④の梁を適当な位置で切って考えれば、絶対に答えにたどり着けます。
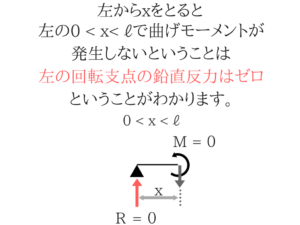
ただ、これでは効率が悪いので可能性があるものを絞っていきます。

左の回転支点は鉛直反力はゼロ！

①と②は左側に鉛直反力が発生してしまうので、この時点でアウト！

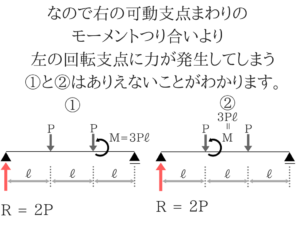
右の回転支点は鉛直反力が2P

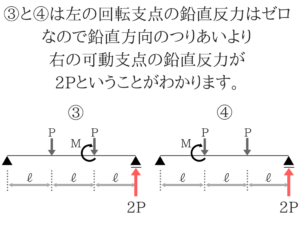③と④に絞って考えていきます。今回はタテのつりあいより簡単に2Pと求めましたが、もちろん回転支点まわりのモーメントつりあいで求めても構いません。

【重要】適当な位置で切って、つり合いを考えてみる！

今③をチェックしていきましたが、このように適当な位置で切ってつり合いを考えてみるという考え方がめちゃくちゃ大事です！

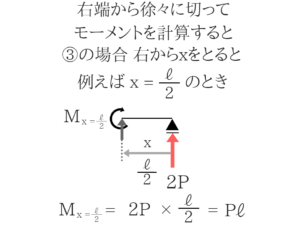
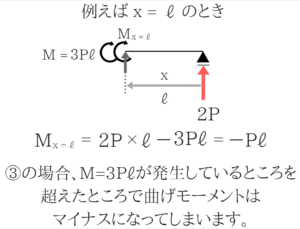
④も切って曲げモーメント図を自分で作ってみる！

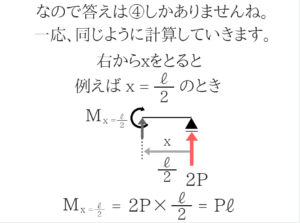
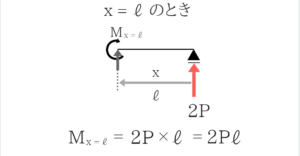
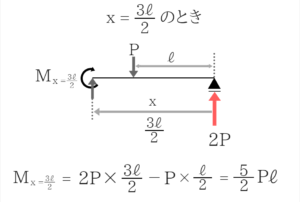
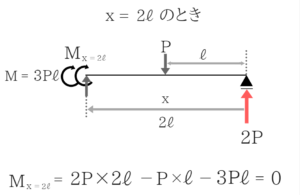X=2ℓのM=３Pℓが発生するぎりぎり前でモーメントつりあいをとると

M_X=2ℓ=3Pℓとなります。

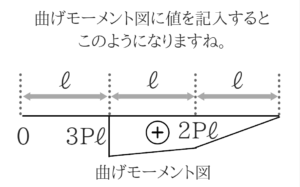
曲げモーメント図のアドバイス

参考に平成28年度の国家一般職の問題No.22で曲げモーメント図の問題が出題されています。
かなり詳しく説明しているのでこちらも参考にどうぞ(^^)

▼平成28年度 国家一般職の過去問解いてみました

切って計算して切って計算してって何回かやれば答えにたどり着けますよね！
曲げモーメントにも慣れてきましたか？
曲げモーメントを使う問題って難しいですが、逆に”理解すると全部解けちゃう”ということです！

【他の受験生は↓の記事を見て効率よく対策しています！】

私が珍しく本気で解説しているから、上の記事はぜひチェックしてくれ！

ココまで勉強したら過去問に挑戦するのもアリです！
実際に出題されている問題を解説しています↓

• →地方上級の過去問をマジ解説！
• →国家一般職の過去問をマジ解説！