「国家公務員の過去問は解答が手に入らない？」
そうなんです。国家公務員の試験の過去問は申請して手に入れることができる（お金がかかります）のですが、過去問の解説は手に入りません！
普通に勉強している人も、独学で勉強している人も過去問の解説がなければ、それは「効率が悪い勉強」となってしまいます！
見ていただいているみなさんに効率よく勉強してもらえるように、私が国家一般職の試験H28、H29の「土木の過去問を２年分」解いていこうと思います！
ではまいりましょう！
地方上級も過去問を２年分解いているので参考にしてみてください。
過去問の入手方法がわからない方はこちらを見てみてください。
目次
- 1 【土木・過去問】国家一般職『平成29年度』マジ解説！
- 1.1 【土木・過去問】国家一般職：No.21「曲げモーメント」
- 1.2 【土木・過去問】国家一般職：No.22「断面２次モーメント」
- 1.3 【土木・過去問】国家一般職：No.23「ひずみ」
- 1.4 【土木・過去問】国家一般職：No.24「たわみ」
- 1.5 【土木・過去問】国家一般職：No.25「浮力（喫水）」
- 1.6 【土木・過去問】国家一般職：No.26「水の衝突力」
- 1.7 【土木・過去問】国家一般職：No.27「マニング」
- 1.8 【土木・過去問】国家一般職：No.28「有効応力」
- 1.9 【土木・過去問】国家一般職：No.29「圧密・体積圧縮係数」
- 1.10 【土木・過去問】国家一般職：No.30「三軸圧縮試験」
- 2 【土木・過去問】国家一般職『平成28年度』マジ解説！
- 2.1 【土木・過去問】国家一般職：No.21「単位荷重法」
- 2.2 【土木・過去問】国家一般職：No.22「曲げモーメント図」
- 2.3 【土木・過去問】国家一般職：No.23「影響線・最大曲げモーメント」
- 2.4 【土木・過去問】国家一般職：No.24「曲げ応力度」
- 2.5 【土木・過去問】国家一般職：No.25「オリフィス」
- 2.6 【土木・過去問】国家一般職：No.26「流れの状態」
- 2.7 【土木・過去問】国家一般職：No.27「跳水現象」
- 2.8 【土木・過去問】国家一般職：No.28「クイックサンド」
- 2.9 【土木・過去問】国家一般職：No.29「室内せん断試験」
- 2.10 【土木・過去問】国家一般職：No.30「時間係数・圧密度」
- 2.11 関連
【土木・過去問】国家一般職『平成29年度』マジ解説！
平成29年度の問題はこの１０問です！
【構造力学】
【水理学】
【土質力学】
本気で解説していきますのでよろしくお願いいたします！
ではいきますよ！
【土木・過去問】国家一般職：No.21「曲げモーメント」
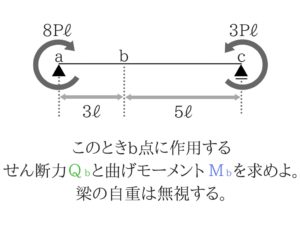No.21は曲げモーメントとせん断力を求める基本的な問題ですね。
基礎がきちんと理解できているのであれば非常に簡単な問題となります。
わからない人はこの問題を復習して覚えてしまいましょう！
曲げモーメントが作用している梁のポイント
では解いていきます！
計算した結果、符号がマイナスだったので反力は上向きではなく下向きということがわかりました。 b点にはせん断力と曲げモーメントが作用しています。 よくある間違いに『曲げモーメントの大きさに距離をかけて計算してしまう×』というものがあります。 ▼曲げモーメントが苦手な方はこちら No.22は断面２次モーメントの問題ですね。超頻出分野です。 三角形の図心軸に関する断面２次モーメントは暗記していなければいけません。 公式が覚えにくいのでできなかった人も多いかもしれませんが、私が今回紹介した断面２次モーメントの公式だけ覚えておけばOKです。 簡単な図形の図心軸に関する断面２次モーメントは絶対に暗記しておきましょう！ No.23はひずみの問題の中でも基礎的な問題です。 勉強している人は正解させたいところです。わからなかった人はこの問題で練習しておきましょう！ ひずみの問題は内容的には難しいですが解法が決まっているんです。 一通りの流れを覚えておけば、実際の問題を解くときにその流れのまま解いていけば答えを求めることができます。 今回の問題を解いて、その解法をマスターしてしまいましょう！ では実際に解いていきます。 使用する公式はこちらの応力度の公式です。 棒の体積はAxなので、重力はAxwとなりますね。 ここで一旦おいておきます。 Δdx/dxというのは微小単位で考えたときの軸ひずみのことなので、 ここまでできたら、あとは計算するだけです。 めちゃくちゃ難しく感じますが、一度解法や考え方をマスターしちゃえば、実際の問題はスラスラ解けちゃうと思います。 難しく感じるかもしれませんが、この問題をマスターしておけばひずみの問題で困ることは少ないと思いますので、実際に出題されたら「ラッキー」って思うようになると思います。 とはいってもばねと一緒に出題されるパターンも頻出ですから取りたい1問ですね。 たわみのポイントから説明します。 文章で書いても理解しにくいと思うので、実際に解いて紹介していきますね！ 合力は(PーF)ということになります。 梁の全長は2Lなので注意が必要ですね。 「ばねの変位（Δ）」というのは「b点でのたわみ（変位）」と等しくなれけばいけません！ 自分でばねの反力をFと置いたのでその力を求めたら、あとはフックの法則を変化（Δ＝の形に）させた式に代入すれば終わりです。 少し難しく感じるかもしれまえせんが、この問題は非常に良い問題なので、一通りの解法は確実にマスターしておきましょう！ 初めてこの問題を解いてみて解けないのは当然です。 公式は この２つです。 ポイントは”重力＝浮力”です。 では解いていきたいと思います。 この公式の浮力と重力を求めて等式でつなげば答えがわかります。 このように物体の底辺からの高さをXとおいてそのまま計算していきましょう。 浮力Fは上向きに作用します。 浮力の問題は「下向きの重力」と「上向きの浮力」がつりあって静止しています。 密度が水と物体とで異なるので注意が必要です。 No.26は水の衝突力の基礎問題です。 有名な問題なので、この問題を通して理解してしまいましょう！ 「流体と壁面間の摩擦を無視すると衝突後も速度が変わらない」ということは知っていなければなりませんね。 これが答えです。 難しそうに見えるかもしれませんが、物理の力学の基礎がきちんと理解できていればすぐにマスターできちゃうと思います！ 水の衝突力(基礎)や力学の基礎部分について簡単に勉強したら、いきなりこの問題にチャレンジしてOKだと思います。 No.27は超頻出のマニングの式を使う問題です。 この２つが問われる問題ですね。 とくに径深Ｒの式は忘れがちなので気をつけましょう。 潤辺は分母にあるので値が小さいほど流量は大きくなります。 公式を覚えていればこのように簡単に解くことができます。 マニングの公式は頻出なので公式を絶対に覚えておきましょう！ 有効応力の問題の解法は決まっています。 を使います。 「土の水中単位体積重量＝土の飽和単位体積重量ー水の単位体積重量」です！ シルト層などがある場合はシルトの湿潤単位体積重量を使いましょう。 1[m2]あたりの土の重さ、水の重さが有効応力とイメージするとわかりやすいかもしれません。 重力が下向きにはたらくので、その垂直抗力のようなものです。 有効応力の問題って解き方を覚えてしまったらめちゃくちゃ簡単なんです。 そのうえ頻出なので絶対にできるようにしましょう！ 実際に解いていきたいと思います！ どの公式を使えばいいのかしっかり勉強して見極められるようにしましょう！ 「この問題がきたらこの公式で解く」という感覚を勉強して身につけなければいけません。 当然公式自体は覚えていなければいけません。 では答えを紹介していきますね。 間違えの選択肢を載せてもしょうがないので、正解だけのせておきました。 非排水条件なのでせん断中の土は”体積が変化しない”んですね。 そして密な状態の砂はせん断によって緩い状態になるとき水などを吸収します。 理解できない場合は、とりあえずこの答えを覚えておきましょう！ 平成28年度の問題はこの１０問です！ 【構造力学】 【水理学】 【土質力学】 本気で解説していきますのでよろしくお願いいたします！ ではいきますよ！ No.21は構造力学の単位荷重法をつかう問題ですね。 ”単位荷重法で解く”という考えが出てこなかった時点で解くのは難しいでしょう。 実際に解いていきますね！ ※節点法ではなく、力のつり合いの関係から、軸力を求めます↓（節点法は誤り） あとは公式に当てはめるだけですね。 値を代入していけば終わりですね。 この問題のポイントは’’単位荷重法を使うということに気づく’’ことです。 この問題を見た時に「単位荷重法」という解法が頭に浮かぶことがまず第一歩です。 公式の使い方は何回も解いて覚えていきましょう！ まずは支点に作用する反力を図示します。 モーメントのつりあいを考えるときははたらく力に十分注意しましょう！ そして、モーメントのつりあいよりE点での反力は上向きということがわかります。 水平反力の向きも両方左むきということがわかりましたね。 仮にE点で最初に矢印を下向きに置いたときは、マイナスがつくのでそれで判断できます！ では反力が求まったので適当なところで切ってモーメントとせん断力をその都度求めていきます。 曲げモーメントの大きさは”力 × 距離”ですからね。 例えばX = 0のときはM=0、 このように距離に比例して大きくなっています。 最終的にせん断力図と曲げモーメント図はこのようになります。 要所要所で計算して出た値を、線でつなぐだけですね！ 『せん断力』に関しては 『曲げモーメント図』に関しては 比例しているので線で結んだものが曲げモーメント図となります。 今回はかなり詳しく説明していますが、実際は答えの概形さえわかればOKです。 そもそも5択で選ぶ問題ですから特徴があるところを切って調べれば答えは早く見つかります。 ▼曲げモーメント図の解説はこちら 今回は問題の指示に従って【(1)影響線を使って解く解法】と【(2)強引に切って計算して求める解法】の２つを紹介していきたいと思います。 影響線をつかいこなせるのであれば、こちらの解法の方がらくです。 絶対値で考えるので、反対の符号を掛けるときだけマイナスをつけてください。 これで最大せん断力はわかりましたね。Qmax＝11.4[kN]です。 次は最大曲げモーメントを同じように求めていきます。 最大曲げモーメントの答えMmax＝258[kN・m]ですね。 ポイントは、パターンを分けて考えることと、三角形の比で影響線の値を求めることですね。 では次に強引に切って最大値を探す方法を紹介します。 問題ももう一度のせておきます。 公務員の試験では、問題に従わずに自力で答えを探しだす力も大事なんですね。 5択の試験なので、どんなやり方で解いたって答えさえ見つけることができればOKです。 ①から反力を求めていきます。 計算して出た値の中から最大のものを選べばOKです。 ちゃんと理解していれば、このように強引に答えを探すこともできます。 曲げ応力度の公式は覚えている人が多いかもしれませんが、使い方をきちんと覚えなければ意味がありません。 まずは公式から再確認しておきますね！ まず引張応力度が最大となる点を求めます。 断面２次モーメントＩと中立軸からの距離yはどの点でも等しいので、曲げモーメントが最大となるＣ点で引張応力度が最大となります。 この曲げモーメントMの大きさを求めるために、支点反力を求めていきます。 もちろん、a点、c点でのモーメントつり合いを考えても反力は求まります。 反力が求まったのでc点における曲げモーメントの大きさを求めていきます！ あとはｃ点での曲げモーメント（最大）の大きさを求めましょう。 公式はこれです。 あとは曲げ応力度の公式に代入すれば終わりですね。 ”曲げ応力度の公式を使う”という事に気づけば簡単な問題となりますが、それに気づかないと難しい問題となってしまいます。 計算自体も単位がバラバラでややこしいですが気を付けて計算していきましょう。 小オリフィスなので流速はトリチェリーの定理で簡単に求まるので㋐は簡単に求めたいところです。 とりあえず最初から説明していきますね！ もちろん、水面では流速と圧力はゼロ、流出口では圧力がゼロとなります。この知識は必要なので絶対に覚えていてくださいね。 次はグラフの形を求めていきます。 まずは（排出量を流量として）補足説明からいきます。 この問題では単位がありませんが、適当において考えたほうがイメージしやすいかもしれません。 補足説明を踏まえたうえで式をたてていきます。 dh/dtというのは傾きとなります。 ちょっと難しかったですかね？ そもそもオリフィスの問題は難しい問題が多いです。 ㋐を理解しているだけで選択肢は1か2に絞れます。 そしてdQの２つの式は公式として覚えてしまっていいレベルです。 No.26は流れの状態の問題です。 過去に何度も出題されている問題で、特徴を覚えていれば見た瞬間解けますね。 初めて解いてみてできなかった人は次見たらできるように勉強しておきましょう！ No.27は跳水現象の問題です。 では答えをのせていきます！ ㋒に関しては少し迷った人もいると思いますが、’’跳水区間でなにか損失があるはずだ’’と考えることができれば答えはすぐにわかりますね。 基本的な考えですが、エネルギーは流れの方向で減少するのが一般的です。 摩擦による損失から断面に関する損失など、何かしら損失があるのでエネルギーが増えるということはほぼないです。 跳水現象は頻出項目のひとつです。 この問題も基礎知識だけで解けてしまう問題なのでできた人もできなかった人も、今一度基礎知識を勉強しておきましょう。 この問題の答えを基礎知識として覚えればOKです。 ミスが多いところなので気をつけていきましょう！ まずは公式から紹介します。 ※動水勾配というのは距離と損失水頭(分子)の比のことです。 解法を紹介していきますね！ まずは動水勾配から求めます。 次に限界動水勾配を求めます。 このように距離を整理しておきます。 あとは公式に代入していけばOKです！ 計算自体は簡単ですが、公式の使い方は少し難しいかもしれません。 クイックサンドの問題は公式を覚えているか、また、その使い方を覚えているかという事が問われます。 同じような問題が何度も出題されているので、この問題のようなパターンで出題されたら解けるように準備しておきましょう！ 土の状態を考えてみましょう。 構造物の急速な荷重載荷直後は「圧密が終わってない」ので非圧密、 逆に長時間にわたる安定性は「圧密も排水も終わっている」ので非圧密非排水条件となります。 冷静にどんな状態なのかをイメージすることが大切かなと思います。 ㋐～㋒に関しては土の状態を考えて試験条件を選びましょう。 この問題を解くポイントは３つです。 とくに排水距離を片面か両面かを判断できないと答えが違う値になってしまいます。 これらに気を付けて実際に問題を解いていきたいと思います。 最終沈下量が50[cm]ということは圧密が終わった(100%の)ときに50[cm]沈下しているということです。 一応、圧密度の公式を説明すると、「圧密度＝時間tの沈下量÷最終沈下量×100 [%]」です。 時間係数と圧密度の問題の中でも難しい方の問題です。 今回の問題でしっかりと復習をして次同じような問題が出た時に確実にとれるようにしておきましょう！ 以上で国家一般職・土木編の過去問解説は終わりです！ 【他の受験生は↓の記事を見て効率よく対策しています！】 
今までずっと回転させる力は「力×距離」だと言ってきましたよね！
単位の部分を意識してみるとうまく理解できるかもしれません。時計回りの力＝反時計回りの力
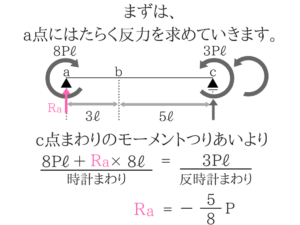とりあえずa点での反力を上向きにおいて計算しました。
これは適当に文字でおいておけばOKです！力を図示(反力の向きに注意)
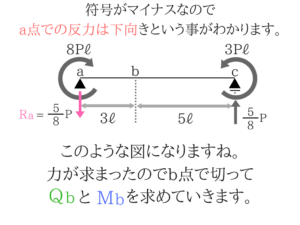
b点で切って考えてみる
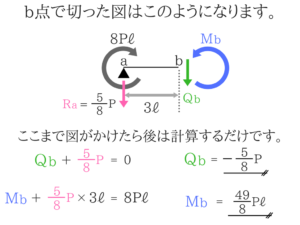Mbを求めるときも「時計回りの力」＝「反時計回りの力」で計算しています。
Qbは鉛直方向のつり合いだけで求まります。曲げモーメントが作用している梁のアドバイス
「曲げモーメントの大きさ＝力×距離」で求められるので勘違いしやすいです。
今回の問題でいう8Pℓや3Pℓは曲げモーメントの大きさで、これはすでに計算された値（回転方向も決まっている）ということです。
⇒なのでモーメントのつり合いをとるときに、8Pℓや3Pℓなどはそのまま値を使えばOKです！
▼曲げモーメントの基礎はこちら【土木・過去問】国家一般職：No.22「断面２次モーメント」
公式をきちんと理解していないと解けない問題ですが、公式を使えれば解けるので絶対に落としたくない問題です。断面2次モーメントのポイント
今回の問題で異なる点はyですね。
これは絶対に覚えておきましょう！三角形の図心軸に関する断面2次モーメントの公式
図心軸から距離がある！
公式を覚えていたら簡単な問題ですよね。
このレベルの問題は解けるようにしておきましょう。アドバイス
断面２次モーメントは大事なのでしっかりと対策をしましょう！【土木・過去問】国家一般職：No.23「ひずみ」
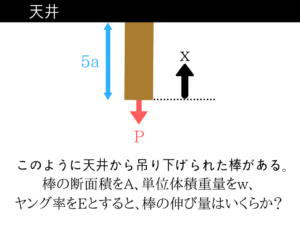
ひずみの問題自体難しい部類なのですが、かなり丁寧な誘導がついています。ひずみの問題を解くポイント
ひずみの公式(応力度)
実際のひずみは公式の中のΔのところです。xで切って、つり合いの式！
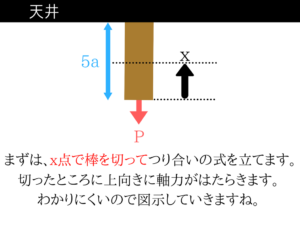
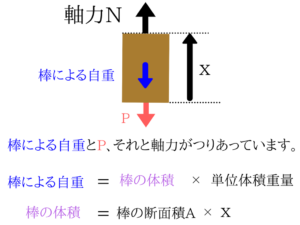単位体積重量に体積をかければ、重力となります。重力はAxw
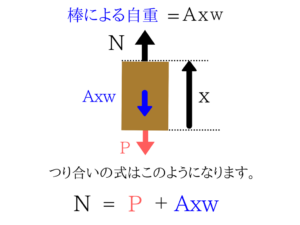
微笑要素dxの伸び量をΔdxとして考える
実際の変位Δというのは、この式を0~5aまで積分したものとなります。後は積分するだけ！
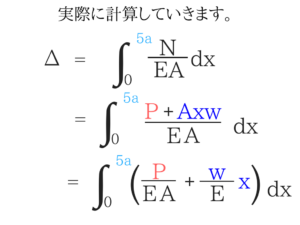
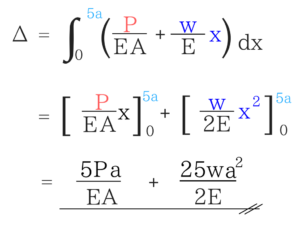
出題される問題がこのパターンしかないので、今回の問題で流れをマスターしておきましょう！アドバイス
【土木・過去問】国家一般職：No.24「たわみ」
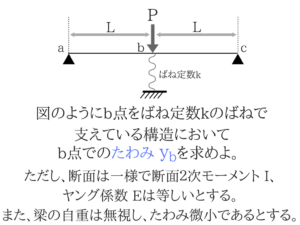
No.24は超頻出のたわみの分野から出題された問題ですね。
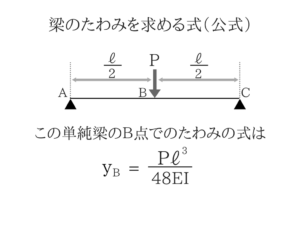
重要な公式の”梁のたわみを求める式”だけでは解けません。たわみのポイント
b点に働く力について考えてみる
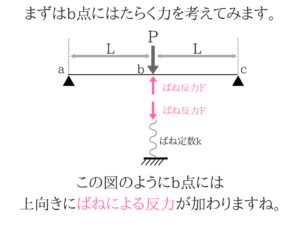
フックの法則を使う！Δはたわみ！
ばね反力が上向きにはたらく！
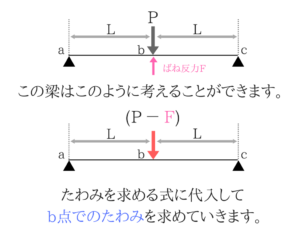
たわみの公式を使ってb点のたわみを求める
ばねの変位＝b点でのたわみ
アドバイス
この問題を理解して次同じ系統の問題が出た時に確実にできるようにしておきましょう！
重要なのできちんと復習しておきましょう！【土木・過去問】国家一般職：No.25「浮力（喫水）」
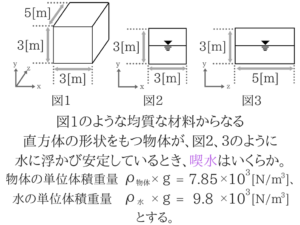No.25は浮力の問題です。
最近浮力の問題が頻出しているので勉強しておいた方がよさそうですね。浮力の問題を解くポイント
ρ(物体の密度)×g×V(物体の体積)＝ρ(水の密度)×g×V(水中の部分の体積)
式で表すとこうなりますね。浮力の問題で使う公式
重力の大きさを求める
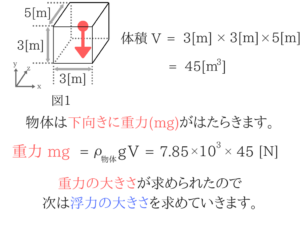
沈んだ部分をXとして、体積を求める
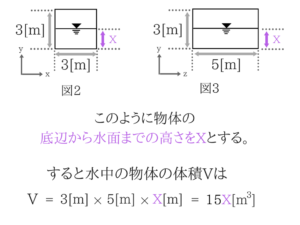
浮力を求めて、「浮力＝重力」
喫水は2.4mとなります。
浮力は水中の体積と水の密度を使うので注意が必要です。アドバイス
この力を図示して計算していきましょう。【土木・過去問】国家一般職：No.26「水の衝突力」
水の衝突力は難しい問題が多いですが、この問題は誘導つきの穴埋め問題です。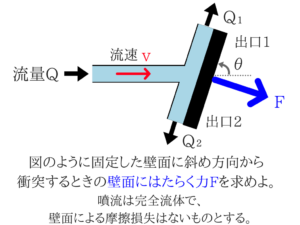
有名な問題がそのまま問題となっているので、問題文は省かせていただきます。まずは流速を分解
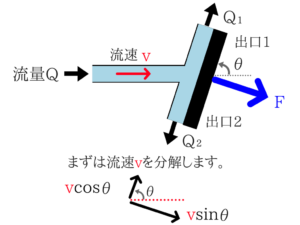
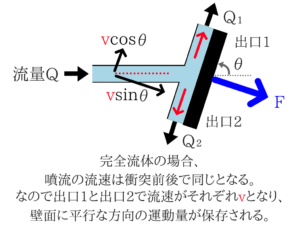
(ただ、この問題の場合は問題文に書いてありました。)運動量は保存される
アドバイス
【土木・過去問】国家一般職：No.27「マニング」
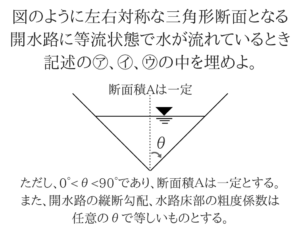
少しひねってある問題ですが絶対に落としてはいけません。マニングの式を使う問題を解くポイント
公式をノートに書いてからこの問題を考えてみましょう！マニングの式と径深Rの公式
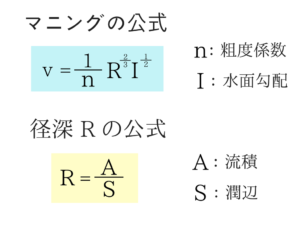まずはこの公式を問題の隅にでも書いておきましょう。vが最大で流量Qも最大、径深Rが最大のとき流量Qも最大
潤辺Sが小さいほど、径深Rは大きくなる
たとえば1/1と1/10では1/1の方が大きくなりますね。潤辺Sが小さいほど、流量Qは大きくなる
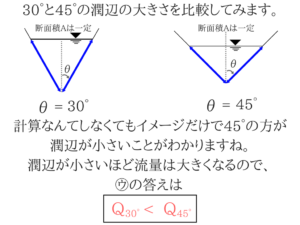
アドバイス
しかも公式を覚えるだけで解けて簡単なので絶対に落とさないようにしましょう！【土木・過去問】国家一般職：No.28「有効応力」
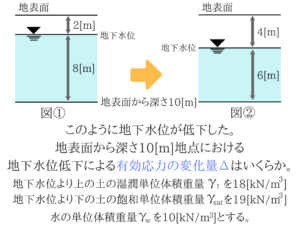No.28は有効応力の問題ですね。最近よく出題されています。
この問題と同じパターンの問題がいくつも出題されているので、この問題を通して有効応力の問題はマスターしてしまいましょう！有効応力の問題を解くポイント
地下水面を基準に考えてみてください。
地下水は土の水中単位体積重量を使う
土や水の重さ≒有効応力
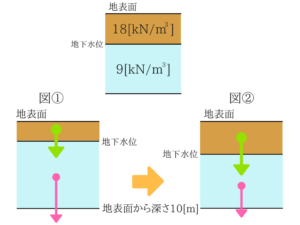図でイメージするとこんな感じですね。重さに対する抗力のことです！
このように図示して考えてみると簡単な問題ですね。アドバイス
【土木・過去問】国家一般職：No.29「圧密・体積圧縮係数」
No.29は圧密の問題ですね
体積圧縮係数の公式を使うことに気づかなければいけませんが、これに気づけば超簡単です。体積圧縮係数の公式を使う
アドバイス
【土木・過去問】国家一般職：No.30「三軸圧縮試験」
No.30は三軸圧縮試験、ダイレイタンシーからの出題ですね。
この分野からの出題は多いので勉強しておくべきですね。圧密・排水条件等の出題も多いです
アドバイス
外部から水が入ってきてほしいがこない。
このように引っ張られる水には負の過剰水圧が発生するわけです。【土木・過去問】国家一般職『平成28年度』マジ解説！
【土木・過去問】国家一般職：No.21「単位荷重法」
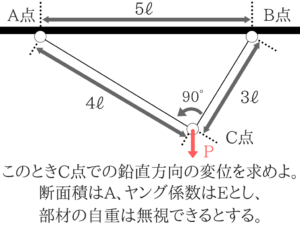
逆に単位荷重法で解くということが頭に浮かんだ場合はものすごく簡単な問題となります。接点法を使ってトラスの軸力を求める！
まずはトラスの軸力を求めていきます。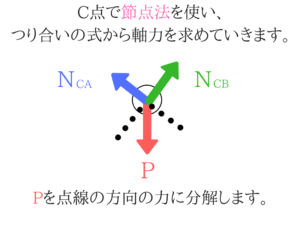
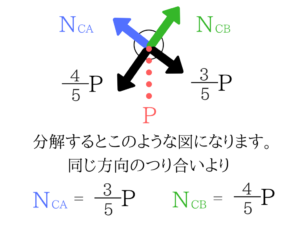３：４：５の三角形なので、これに気づくことができるとすぐに求められますね。
もちろん角度をθとおいて力を分解すればOKです。単位荷重法の公式を使う！
上の線がついているものはP=1としたときの軸力となります。
使い方はあらかじめ勉強しておかなければなりませんが、これに気づくだけで一気に簡単な問題となってしまいます。アドバイス
切って考えてみても全然解けないんですよね。
単位荷重法で解くって後で気づいたときに「あ～なるほど！」って思いました！【土木・過去問】国家一般職：No.22「曲げモーメント図」
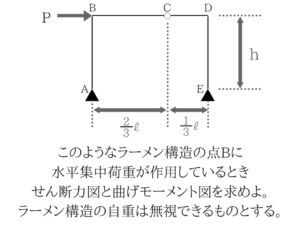No.22はせん断力図と曲げモーメント図の概形を求める問題ですね。
超重要で超頻出の問題です。曲げモーメント図のポイント
では解いていきますね。まずは働く力を図示！
A、E点ともに回転支点なので反力数は２でタテとヨコですね。
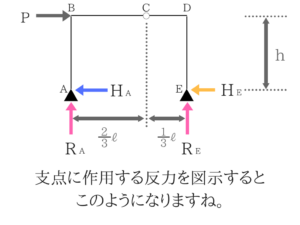この時点ではプラスかマイナスかわからないので、文字だけ置いておきます。
後でモーメントのつりあいをとったときに正負がわかります。反力の大きさを求める！
図示しなおして、モーメントのつり合いを考えてみる！
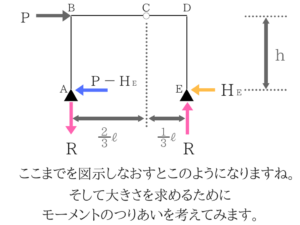
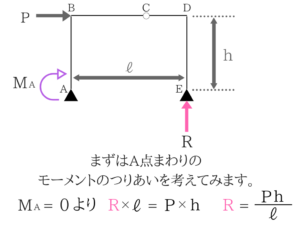
A点に自分がいると思って時計まわりの力と反時計まわりの力を考えると理解しやすいです。計算すると文字の正負がわかる
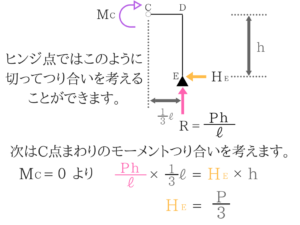
計算すると文字の正負がわかる
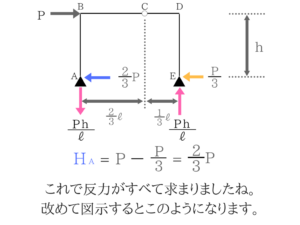
この反力の向きは非常に重要なので、きちんと求められるようにしましょう！
とりあえずは適当に矢印の向きを置いておけばOKです。適当に切って、MとQをその都度求める！
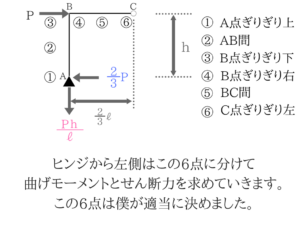
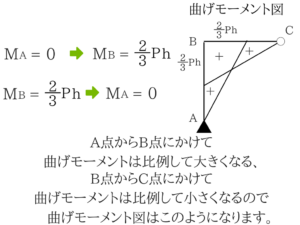
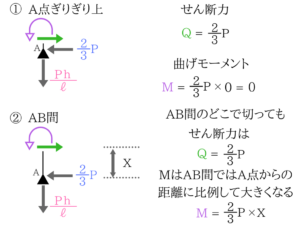曲げモーメントMはAB間ではA点からの距離に比例して大きくなりますね。曲げモーメントは力×距離
X=h/2のときはM=2P/3 × h/2でM=Ph/3、
X=hのときはM=2P/3 × hでM=2Ph/3要所要所で大きさを計算してみる
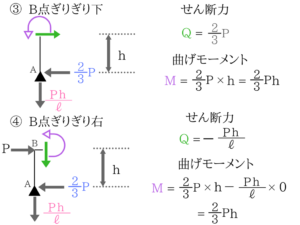
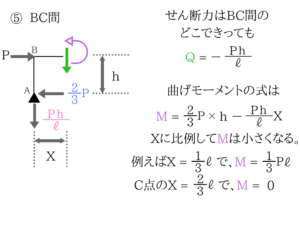BからCにかけてはMは小さくなっていきますね。
最終的に曲げモーメントはC点でゼロになります。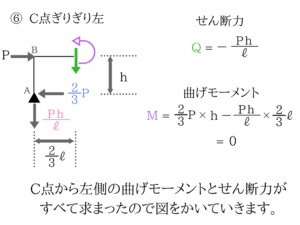
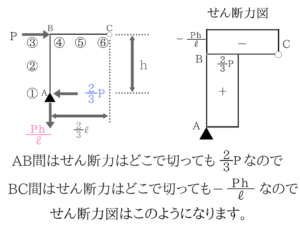
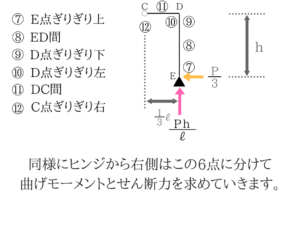右側も同様に求めていけば終わりです。
同じ作業なので説明は省かせていただきます。せん断力図と曲げモーメント図完成
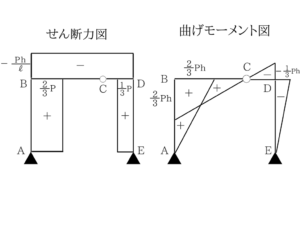
ME＝０からMD＝－Ph/3へ
MD＝－Ph/3からMC＝０へアドバイス
慣れてくれば２、３点適当に切って考ええば答えがわかります。
▼曲げモーメント図の問題はこちら
切ってその都度計算していけば確実に答えを導き出せるんだ。【土木・過去問】国家一般職：No.23「影響線・最大曲げモーメント」
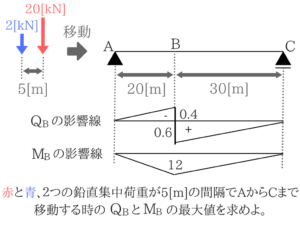No.23は影響線を使う問題ですね。
使い方には慣れていないといけません。(1)影響線を使う解法
まずは最大せん断力を求める！
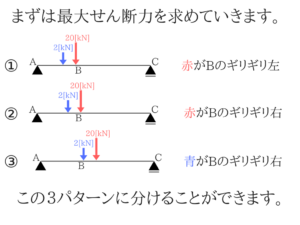
要は大きさだけわかればいいわけです。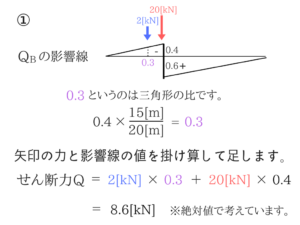
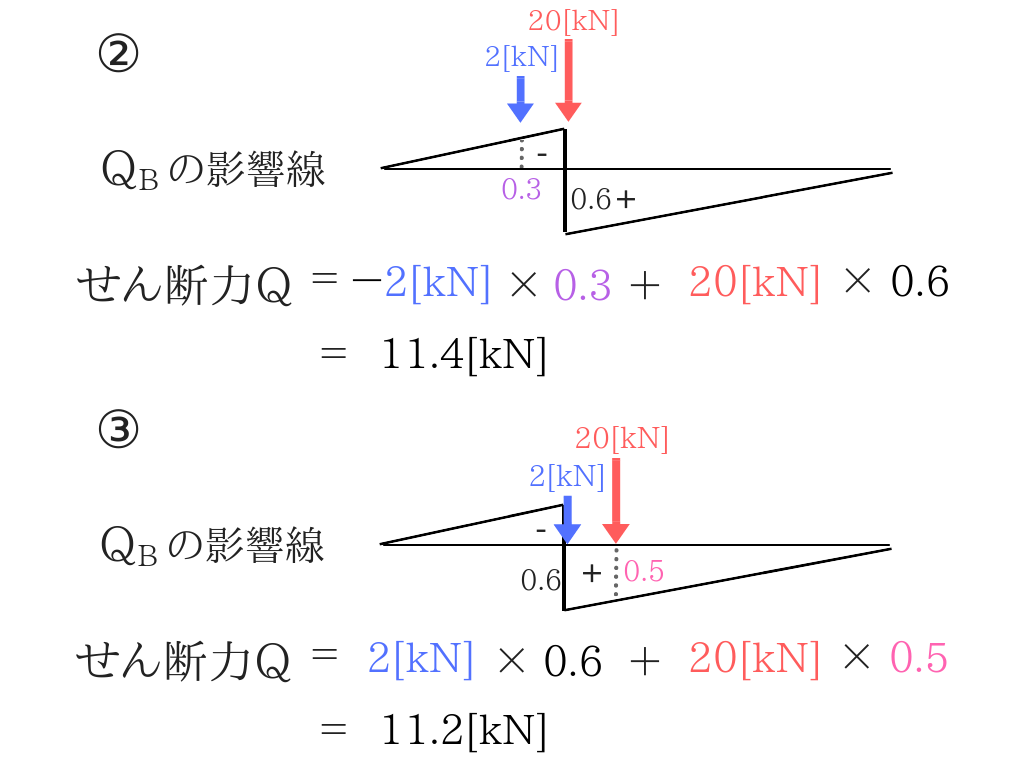
同様に最大曲げモーメントを求める！
今回は２パターンしかありませんね。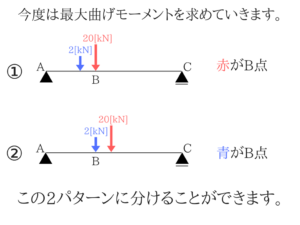
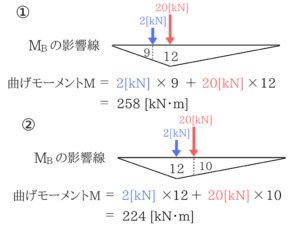
(2)切って最大値を探す解法
解法手順はこんな感じ！
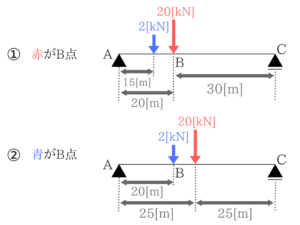
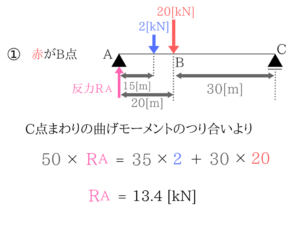
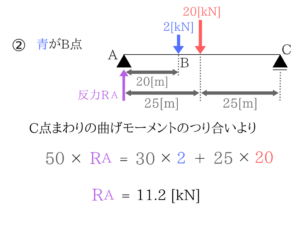今回はA点の反力がわかればいいのでC点に自分がいると思って曲げモーメントのつりあい式を立てればOKですね。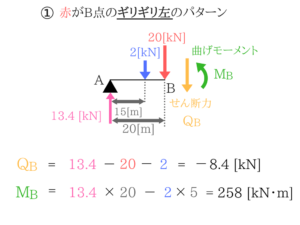
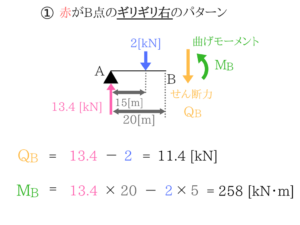
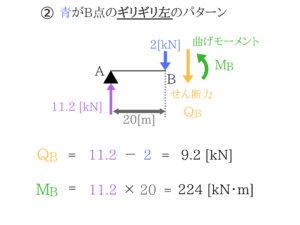
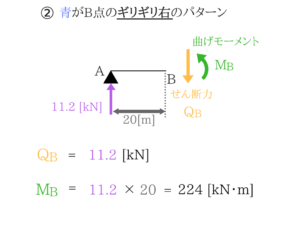
影響線を使わなくても、最大せん断力と最大曲げモーメントを探し出すことができちゃいましたね！【土木・過去問】国家一般職：No.24「曲げ応力度」
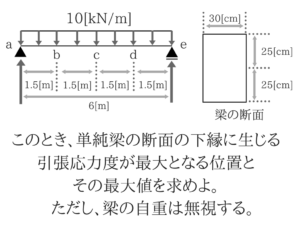No.24は曲げ応力度と断面係数の分野の問題ですね。
公式を覚えてさえいれば解けるのでなんとしても取りたい１問ですね。
今回の問題で使い方をマスターしてしまいましょう！曲げ応力度の公式
引張応力度が最大になるのは…
まぁこれは知らなくてもなんとなくわかりますよね。そう、ど真ん中C点です。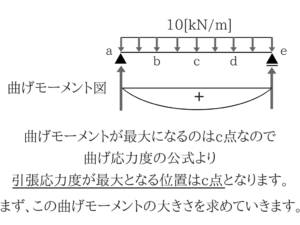
曲げ応力度の公式より支点反力を求める！
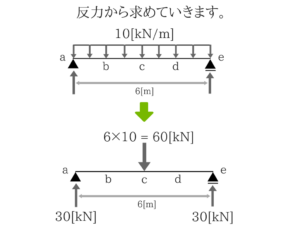梁の真ん中に力が加わっているので支点の反力はa点、e点ともに30[kN]となりますね。曲げモーメントの大きさを求める
c点で切ってモーメントのつり合いを考えればOKです。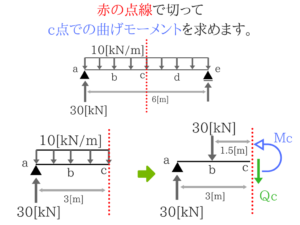
このように切って考えましょう。c点で切ってモーメントつり合い
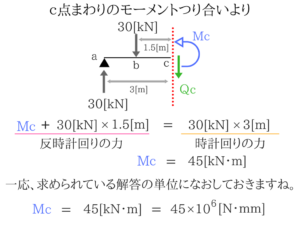最大曲げモーメントが求められたので、Ｉとｙを求めていきます。
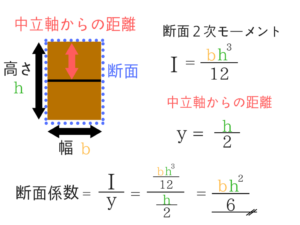
単位をなおしたのは、５択の解答の単位が[N/mm2]だったからです。断面2次モーメントの公式
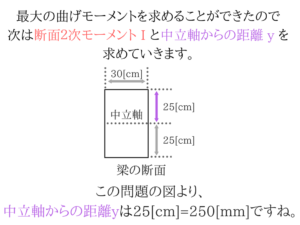
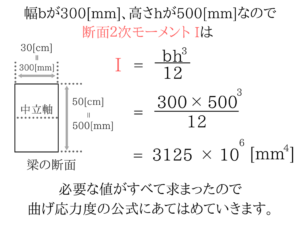ここでも単位をなおしているのは、解答の単位とあわせるためです。曲げ応力度の公式に代入だ！
今回は公式をわかりやすくするためにすべて計算してから代入しましたが、計算する前の形のまま代入したほうが計算はラクです。アドバイス
【土木・過去問】国家一般職：No.25「オリフィス」
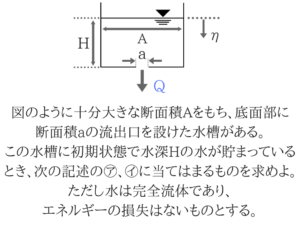
No.25は水理学からの問題でオリフィスの問題です。
オリフィスの問題は全体的に難易度がやや高めです。まずは排出量Qを求める！
完全流体なのでベルヌーイの式の右辺の一番右の項、損失水頭はゼロとなります。グラフの形を求めるために、経過時間tの式を求める。
⇒そのために経過時間ｔの式を求めていきます。
変化量dQ＝面積×dH
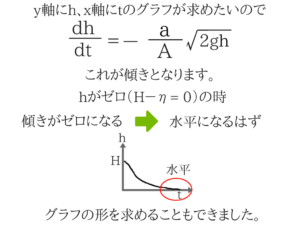
文字が違うとわかりにくいですがx-yグラフでいうdy/dxが傾きということです。アドバイス
ですが、この問題の㋐のように基礎的な出題もありますので、そこはできるようにしたいです。【土木・過去問】国家一般職：No.26「流れの状態」
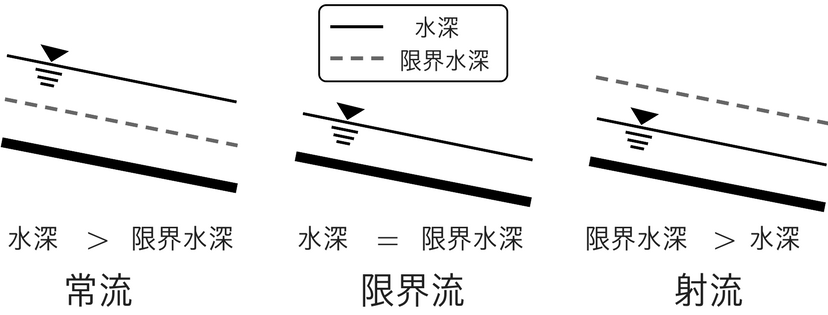
頻出問題なので確実に正解したい１問ですね。アドバイス
この問題は確実にとらなければいけません。【土木・過去問】国家一般職：No.27「跳水現象」
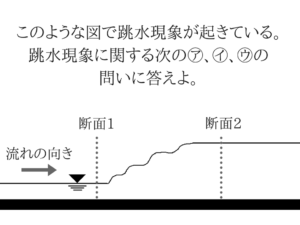
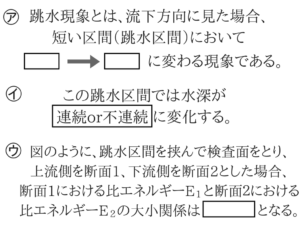
㋐、㋑、㋒のすべてが跳水問題の基礎知識なので確実にとりたいですね。跳水は射流から常流に変わる時に起こる
エネルギーは基本減少する
跳水現象では渦によるエネルギー損失があることは知っておかなければいけません。アドバイス
【土木・過去問】国家一般職：No.28「クイックサンド」
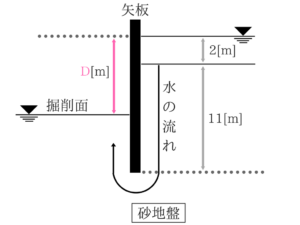
No.28はクイックサンドの問題です。
少し難しいですが、過去に同じような問題を解いていれば解けると思います。
⇒限界動水勾配の公式の分子は’’土の水中単位体積重量’’です。
⇒そして動水勾配の公式の分子も’’掘削面から地下水面までの距離’’なので注意が必要です。クイックサンドの公式
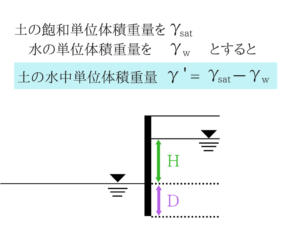
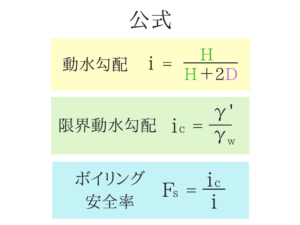公式の使い方を覚えていれば解ける１問です。動水勾配iを求める
※動水勾配の公式は分子の値に注意しましょう。
公式に代入する値に注意が必要です。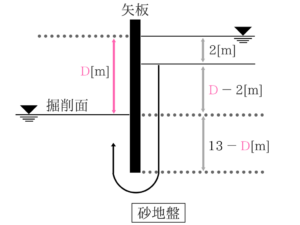
限界動水勾配を求める
公式の使い方が練習しておくようにしましょう。
※動水勾配の分子は『損失水頭』です！水面差のことですね！アドバイス
【土木・過去問】国家一般職：No.29「室内せん断試験」
No.29は室内せん断試験の問題です。
理解するのが難しい分野ですが、最近出題が多いです。室内せん断試験のポイント
「排水も終わってない」ので非排水となります。
㋓に関しては知識問題です。答えをそのまま覚えてしまいましょう！アドバイス
【土木・過去問】国家一般職：No.30「時間係数・圧密度」
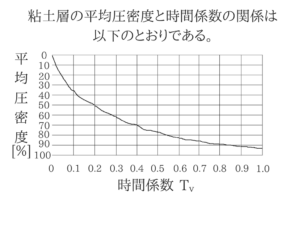No.30は頻出の時間係数からの出題です。
時間係数の問題の中でも少し難しいですが、あらかじめ勉強しておいて確実に点につなげていきたいところです。時間係数・圧密度のポイント
条件をきちんと読み取ろう！
この最大排水距離を間違えてしまうと、計算がすべてくるってしまうのできちんと分けられるようにしましょう。公式を使って時間係数を求めていく！
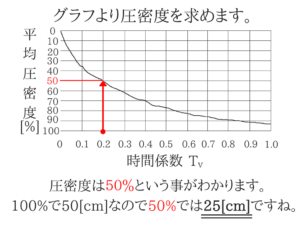
50%しか進んでいないということは単純にその半分で25[cm]ということです。アドバイス
この問題を理解して解くことができれば、この系統の問題はすべて解けると思います。
土木・地方上級編のレベルが同じくらいなので参考になると思います！
この過去問がある程度解けた皆さんは公務員試験も余裕の合格だと思います！
わからなかった部分は↓以下のページで復習しておきましょう！
図の8Pℓや3Pℓは大きさを表しています。(Pは力、ℓは距離)