「公式が使えれば水理学も楽勝♪」
公務員試験に出る『水理学』という専門科目。
内容が他の分野に比べて難しい印象があります。
でも公式を使うだけで解けてしまう問題って実はかなり多いんですね!!
それに、誰かに教えてもらうと超簡単だったり…
勉強が進んでいる方も、そうでない方も効率よく勉強をしてもらえるように、
また、このページを見ただけで水理学を理解していただけるように
僕が重要なところをひとつひとつ”本気で”説明していきます!
長いページとなりますが、お付き合いいただけたら幸いです。
土木職公務員試験 専門問題と解答 [必修科目編]
今回は水理学編です。
水理学と土質力学を勉強したい人はこちらをみてくださいね。
- ⇨勉強シリーズ 構造力学編
- ⇨勉強シリーズ 土質力学編

このページを見ただけで、勉強難易度が一気に低くなると思います!!
目次
【公務員試験の水理学】参考書のタイトルごとの重要度
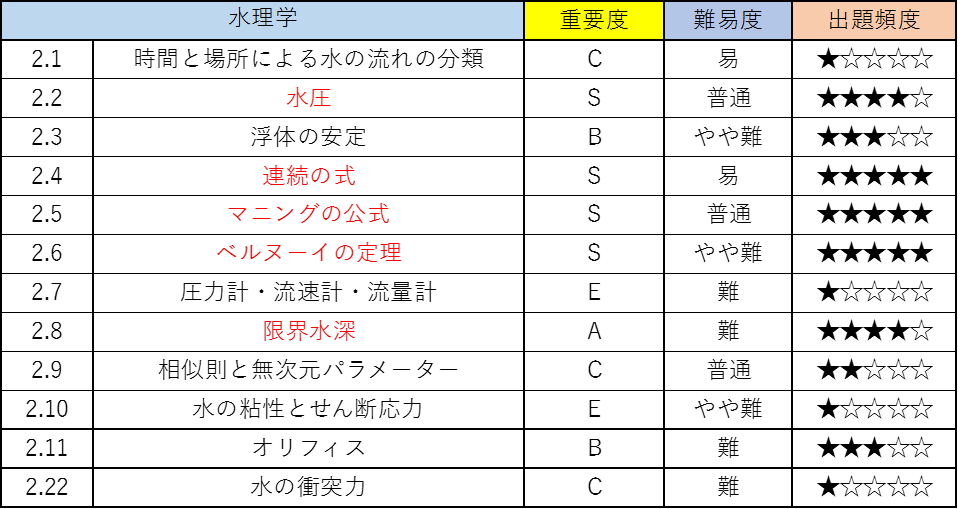
重要度はSが超大事な箇所で残りはA~Eの5段階で示してあります。
今回も重要なところは理解してもらえるように図で細かく説明し、効率が悪い問題の説明は省かせていただきます。
”重要だけどわかりずらい”
そんな問題は実際の問題を解きながら公式の使い方や、水理学の考え方を説明していきたいと思います。
【水理学】①時間と場所による流れの分類

『流積と潤辺がどこを表しているのか』という事はきちんと理解しておきましょう!
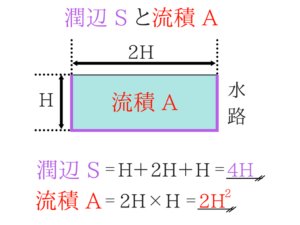
流れの分類は教科書通りにおぼえましょう!

絶対に覚えておいてください!
【水理学】②水圧

水圧は水理学の基礎となるので、確実に理解してください!
非常に重要な項目となりますので、図を使ったり問題を解いたりして詳しく説明していきます!
水圧 ★★★★★
ここは簡単に読んでおく程度でよいでしょう。
実際に水圧が図示できるようになるほうが、文章で覚えるよりよっぽど大事です。
水平な平面に作用する全水圧 ★★★★★
- 全水圧の大きさは、三角形の面積ということです!
- そして三角形の重心は水面から2/3の位置にあります!
全水圧と静水圧、きちんと区別できるようにしましょう。
大事なので図でわかりやすく説明しますね。
全水圧の求め方
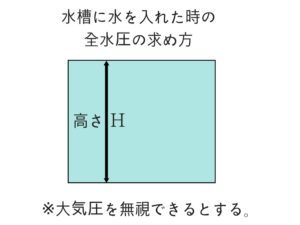
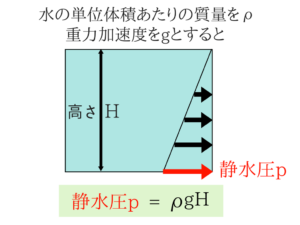
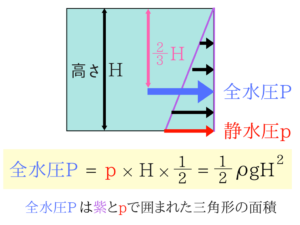
このように全水圧は水面から2H/3のところ(重心)に作用しますね。
赤の矢印が静水圧、青の矢印が全水圧となります!

絶対圧とゲージ圧 ★★★★★
水圧のところで説明しましたが、大気圧を考慮しなければならない問題と、大気圧を考慮しなくてもよい問題があります。
問題文にきちんと書いてあるので使い分けてくださいね。
圧力水頭 ★★★☆☆
これは別に覚えていなくても大丈夫です。
先ほどの静水圧の公式のH=に変換したものを圧力水頭(H=p/ρg)と呼びます。
傾斜した平面に作用する全水圧 ★★★☆☆
公務員試験では、「斜面した平面に作用する全水圧を求めよ」「全水圧の作用点を求めよ」といった問題が出題されます。
水圧の基礎となりますし、土木系の科目の考え方の基礎ともなりますので、きちんと使いこなせるようにしておきたいところです!

水圧について理解してもらうために、以下の2問を解いていきます。
実際に出題された問題を解きながらポイントを説明していきますね!
- 斜面の問題
- 全水圧の作用位置の問題
(1)斜面の水圧の解き方
斜面でも水圧は面に垂直に作用します。
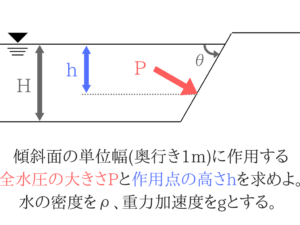
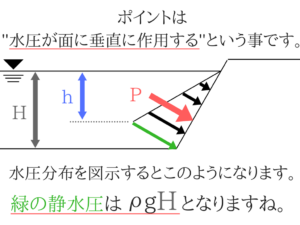
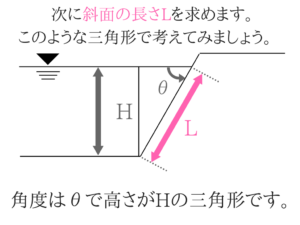
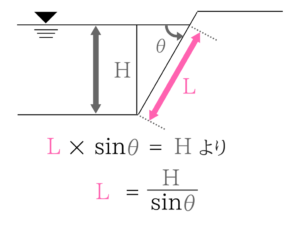
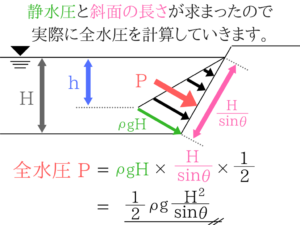
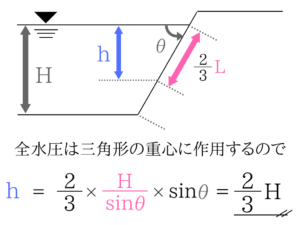
計算自体は普通の水圧と同じですね!
斜面でも水圧は垂直に作用するということをきちんと理解しておきましょう。
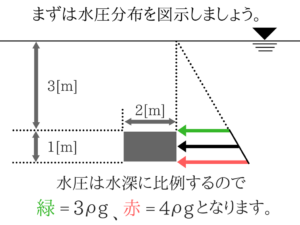
(2)台形分布する場合の水圧と作用位置
台形分布は三角形と四角形に分けて考えていきましょう!
全水圧を求める場合に水圧分布が台形になるものがあります。
静水圧の作用点の位置を見つける問題です。
実際に出題された問題を解きながら作用位置を求めてみますね。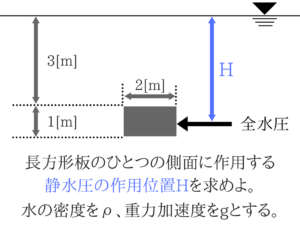
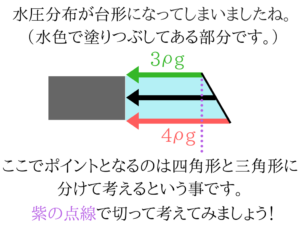
台形部分は三角形と四角形に分けて考える(鉄則)
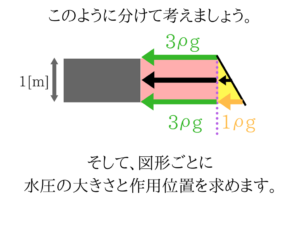
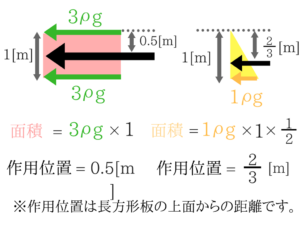
水圧の大きさは図形の面積なので、四角形は3ρg、三角形は0.5ρgとなりますね。
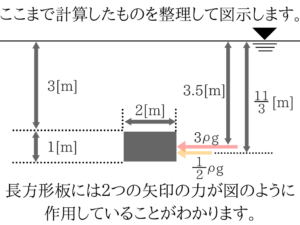
四角形は3+0.5で3.5[m]、三角形は3+2/3で11/3[m]が力の作用位置となります。
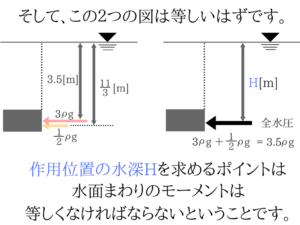
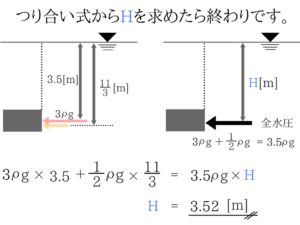
少しごちゃごちゃした説明になってしまいましたが、台形の水圧分布は三角形と四角形にわけて考えると簡単に考えることができます。
【別解】(2)台形分布する場合の水圧と作用位置
今解いた台形分布する水圧の作用位置の問題、実は公式を使いこなせれば一発で答えを求められるんですね。
一応、こっちの解法も紹介しておきます。
全水圧の作用位置の公式

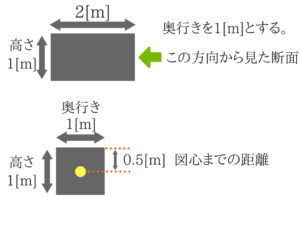 断面積と断面2次モーメントは奥行きを使用しますので、注意してください。
断面積と断面2次モーメントは奥行きを使用しますので、注意してください。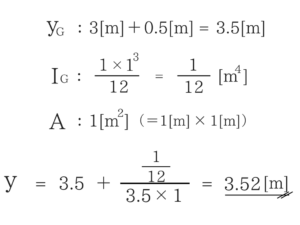 使い方が難しいので、基本的にはこの解法は使わずに、先ほど紹介した普通の解法で答えを導いて下さい。
使い方が難しいので、基本的にはこの解法は使わずに、先ほど紹介した普通の解法で答えを導いて下さい。
曲面に作用する全水圧 ★★★☆☆
- 鉛直分力と水平分力の求め方をきちんと理解しましょう!
- 奥行きを1[m]と自分で置くのがコツです。
テンダーゲートの問題がたまに出題されます。
曲面に働く水圧の公式
まずは公式から載せておきます。
使い方が難しい公式ですので、実際に問題を解きながら説明していきますね。
円弧型のゲートの問題
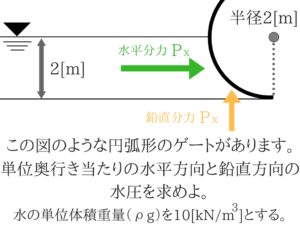
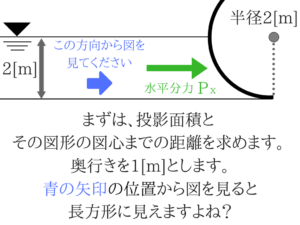
奥行きを1[m]と置いて考えましょう。
奥行1mと仮定して実際に青部分から見ると…
そして、青の方向から見た図形が投影図形となります。
タイヤを前から見ているようなものなので、長方形になりますよね!
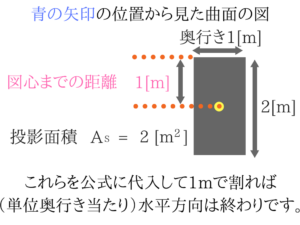
公式を使って水平分力を求める

公式を使って鉛直分力を求める
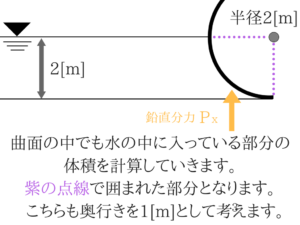
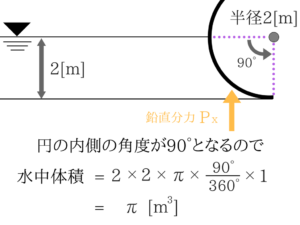 半径×半径×πで面積、それに奥行きの1[m]をかけて体積となります。
半径×半径×πで面積、それに奥行きの1[m]をかけて体積となります。
そして角度が90°なので体積は90/360で1/4となりますね。 一度やり方を覚えてしまったら簡単だと思います。
一度やり方を覚えてしまったら簡単だと思います。
そんなに出題は多くないですが、一応抑えておきましょう。
【水理学】③浮体の安定

最近はよく浮体のつり合いの問題が出題されています。流行っているかもしれませんね。
この項目は昔の教科書には記載されてないのですが、教科書を改訂した際に増加された項目ですからね。
浮力の問題を解くポイントは”浮力”と”重力”がつり合っているということです!
 工学の基礎や、教養試験の物理でも出題されます。
工学の基礎や、教養試験の物理でも出題されます。
参考書の問題をいくつかといておくとよいでしょう!
【水理学】④連続の式

連続の式はめちゃめちゃ大事です。
- どの断面でも流量が等しいということです。
- 断面積が大きければ流速は小さく、断面積が小さくなれば流速は大きくなります!
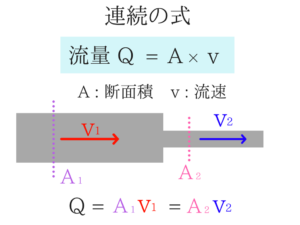 この先の項目の基礎となる公式なので絶対使いこなせるようにしましょう!
この先の項目の基礎となる公式なので絶対使いこなせるようにしましょう!
様々な分野で使用します!

確実に使いこなせるようにね!

ちゃんと勉強しておくよ!
【水理学】⑤マニングの式
マニングの公式を使って解く問題は地方上級、国家一般職で超頻出です。 公式はこちらです。 流積と潤辺をきちんと求められるかというのがマニングの問題をとくカギとなるので絶対に覚えてください! 問題を解く前に注意しなければならない点があるので説明します。 たまに問題文に などと書いてある問題があります。
使い方自体は簡単なので、実際に出題された問題を解いていきますね。マニングの公式
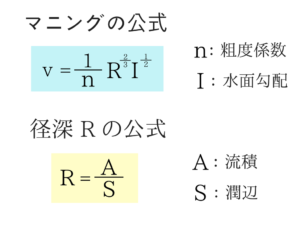

マニングの公式を使う際の注意点
このような場合は”水路幅=潤辺”と考えて問題を解く必要がありますので、注意して問題文を読んでくださいね。
マニングの公式を使う問題
では問題を解いていきましょう!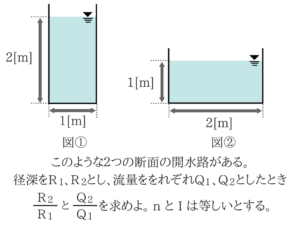
要は、径深Rと流量Qをそれぞれ求めよということです。
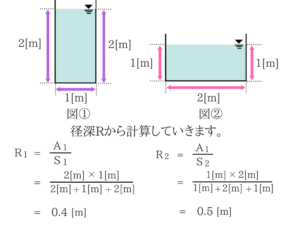

流量を求めるときはマニングの公式を使ったあと、連続の式から求めます。
マニングの式で平均流速を求める
マニングの式は「平均流速v」を求める式です。
Q=Avに代入して流量を求めていきましょう。




慣れてしまえばどうってことないけどね!
【水理学】⑥ベルヌーイの定理
ベルヌーイの範囲からの出題もかなり多いです。しっかり勉強して理解する必要があります。

⇒きちんと使いこなせるように勉強していきましょう!
- ベルヌーイの定理を使って解く問題
- エネルギー線と動水勾配線の問題
- 損失水頭の問題
では、頻出項目のところを細かく解説していきますね。

絶対に考え方・公式をマスターしよう!

俺でも理解できるようにわかりやすく説明よろしくな!
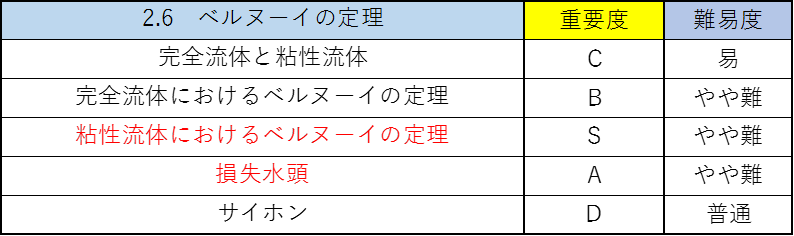
完全流体と粘性流体 ★★☆☆☆
ここは軽く読んでおく程度でよいでしょう。
完全流体におけるベルヌーイの定理 ★★☆☆☆
『エネルギー損失は無視する』などの記述がある場合のみ、こちらの公式を使用します。
次の項目で説明する粘性流体のほうの公式を覚えてください。
そのほうが理解しやすいと思います。
粘性流体におけるベルヌーイの定理 ★★★★★
粘性流体におけるベルヌーイの定理は非常によく使用します。
仮に「エネルギー損失を無視する」という記述があった場合でも、hのところにゼロを代入すればOKです。

ベルヌーイの定理のを使って解く問題とエネルギー線と動水勾配線の関係の問題を解いていきますね!
ベルヌーイの定理の使い方ポイント
ベルヌーイの定理の公式を使うポイントは3つあります。
- 水面では流速vと圧力pはゼロとなります!
- 2つの点を選択してベルヌーイの定理の式に当てはめます。
- その2つの点でのつり合い式を立てるということですね
損失水頭はなにかというのが問題を解くポイントです。
例えば、”高いところ”から”低いところ”に物体が動いた場合、エネルギーの損失があります。
(高いところのエネルギー)-(エネルギー損失)=(低いところのエネルギー)
高いところの方がエネルギーが大きいです。円管の摩擦などでエネルギーが使われて、低いところの小さなエネルギーとなるわけです。
ポイントの補足説明
きちんと理解していただきたいので、ポイントの説明からいきます!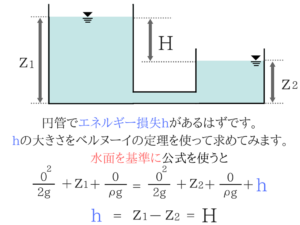
この場合、水面の高さの差がエネルギー損失の大きさとなるわけですね。

ポイント①の水面での流速vと圧力pはゼロになる、ポイント③のエネルギーについての考え方
これらを覚えてから問題を解いていきましょう!
ベルヌーイの定理を使って解く問題
では実際の問題にいきますね。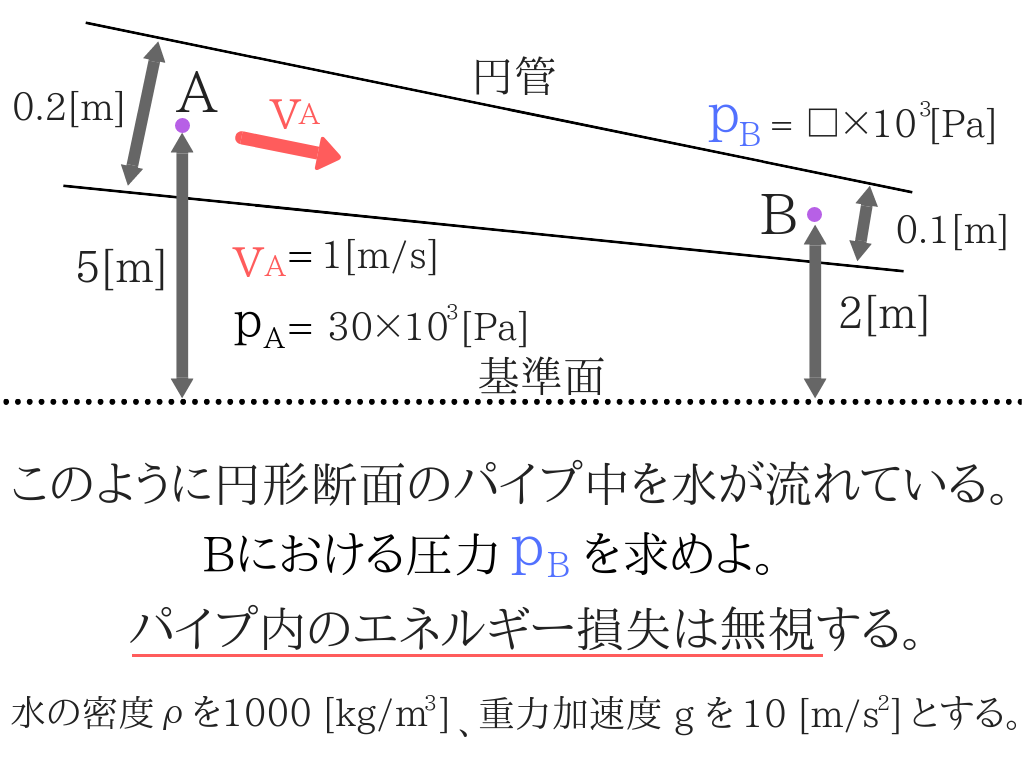
今回はエネルギー損失がゼロなので、わからない値はB点の流速だけですね。

”エネルギー損失は無視する”という記述があるので、hℓにゼロを代入します。

このように式さえ立てることができれば、あとは計算をするだけですね。
エネルギー線と動水勾配線の問題
エネルギー線と動水勾配線の関係のポイントをまとめて書いておくのでメモしてくださいね。
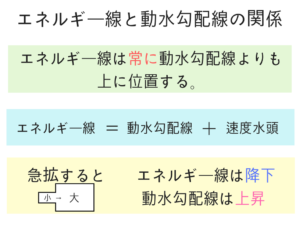 この特徴を覚えておくだけで実際の問題もほとんど解けてしまうでしょう!
この特徴を覚えておくだけで実際の問題もほとんど解けてしまうでしょう!
- エネルギー線は水面より下に位置する
- 最初の位置より上に上がることはない
このような点も覚えておく必要があります。
実際に教科書の問題を、ポイントを覚えたうえで解いてみましょう!

簡単だから絶対ポイントを覚えておこう!

実際の問題も見てみたけど、せんせいの説明だけで解けたわ!
損失水頭 ★★★★☆
損失水頭も出題が多い分野となります。
- (1) 形状変化による損失水頭
- (2) 円管での摩擦損失水頭
こちらの項目を順番に説明していきますね!
(1) 形状変化による損失水頭
混乱しがちですが、公式に使う流速は”断面1の時の流速v1”です! とりあえずこの公式の使い方はおさえておきましょう! 円管での摩擦損失水頭の問題は基本的にはベルヌーイの定理を使用して解くものがほとんどです。ベルヌーイの定理の使い方をもう一度確認してみましょう! 円管での摩擦損失水頭の公式はややこしいので、実際に問題を解いて説明していきます! 問題はこちらです。 まずは公式からのせておきます! この問題を解くためには’’ベルヌーイの定理’’を使わなければならないんですね。 ベルヌーイの定理は2点を選んで使います!そして この2つが問題を解くポイントとなります! 最後に文字に数値を代入して終わりです。 円管での摩擦損失水頭の公式とベルヌーイの定理の使い方はきちんと理解しておきましょう! 公式さえ覚えてしまえば、もしサイホンの問題が出た時に一発で解けますが、出題は少ないので、余裕がある人だけ公式を覚えておきましょう。 公式に数値を当てはめるだけなので説明は省かせていただきます。 この分野は出題もほぼないですし、出題されても難しいので飛ばしましょう! この分野を勉強する時間があるなら、もっと他の重要度が高い分野を勉強しましょう。 この分野からもかなり出題されています。 比エネルギーや限界水深に関する問題は少し難しいですが、勉強しておいたほうがいいです。 常流と射流、それに跳水のところは簡単なうえにかなり出題されるので絶対勉強してください。 全体的には少し難しい分野ではありますが詳しく説明していきたいと思います! 比エネルギーは次のEQ曲線のところで限界水深などを算出する際に多く使用するので、次の項と併せて詳しく説明します。 E-Q曲線やQ-H曲線の特徴は覚えておいたほうがいいです。 E-Q曲線やQ-H曲線の特徴を知っていれば解ける問題も出題されていますので、特徴はおさえておきましょう! 限界水深は比エネルギーが最小となる条件(dE/dH=0)から求められます。 では「限界水深を求めよ」という問題の解法を実際に解きながら説明していきますね。 27=3の3乗となりますので(33)2で36、わかりやすいように並べ替えて33×33で93としています。 簡単な分野なんですけが、頻出項目となります! わかりやすく図を作ってみました。 常流では水深が高いので流れはゆっくり、射流では水深が低いので早い流れとなります。 実際にイメージしておくことで、ミスが減らせると思います。 射流から常流に変わるときに跳水現象が発生します! 跳水現象の問題も単純なのに意外と出題されます。 勾配を傾けていって、水深が限界水深と一致したときの勾配を限界勾配といいます。 そして、このときの流れを限界流といいます。 参考書を簡単に読んで覚えておきましょう! フルード数の問題自体はたまに出題される程度ですが、フルード数と常流、射流、限界流の関係はよく出題されるので教科書の表を覚えておきましょう。 フルード数の公式と、常流と射流などの関係を図で説明していきますね! 特にこの関係は非常によく出題されているので覚えておくとよいでしょう! 出題はかなり少ないと思います。 今回は説明は省かせていただきます。 オリフィスの問題は難しいものが多いですが、 理解するのが難しいと思うので、実際の問題を解きながら詳しく説明していきます! ”流量Qの単位は[m3/s]”です。 では問題いきます! この問題解きはじめる前に補足説明をさせていただきます。 これを理解したうえで問題にいどみましょう! かっこの中は√h2-√h1となりますが、かっこの外にマイナスがあるので中身が逆になりますね。 難しそうに見えるかもしれませんが、文字の意味を理解するとやっている計算自体は単純となります。 水の衝突力の問題は少し考え方が難しいですが、なるべくわかりやすく説明していきたいと思います。 簡単な問題と、実際に出題された斜面への噴流の問題の2問を解いていきます! まずはポイントの補足説明から紹介します! これだけ説明されてもわかりませんよね。 ポイントをうまく理解してもらうために基本的な問題を解いていきます! (大気に噴流する場合圧力の差は生じません。) この公式は覚えておいてくださいね。 赤の矢印の部分を物体として考えて、壁にぶつかったと考えるとわかりやすいと思います。 次は実際に国家一般職で出題された斜面への噴流の問題を解いていきます。 「流体と壁面間の摩擦を無視すると衝突後も速度が変わらない」ということは知っていなければなりませんね。 ただ、この問題の場合は問題文に書いてありました。 少し難しいと思いますが、国家一般職で実際に出題されたときは誘導付きの穴埋め問題でした。 運動量に関しては工学の基礎と一緒に勉強しておいた方がいいと思います。 【他の受験生は↓の記事を見て効率よく対策しています!】 私が珍しく本気で解説しているから、上の記事はぜひチェックしてくれ! ココまで勉強したら過去問に挑戦するのもアリです! 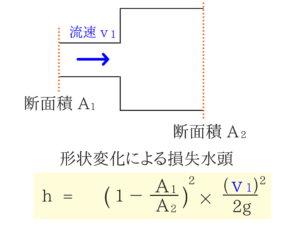
(2) 円管での摩擦損失水頭
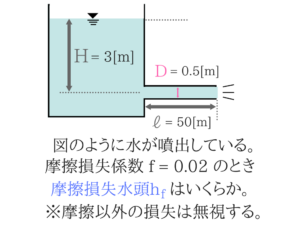
 この公式を使いたいのですが、公式だけ使えればいいわけではありません。
この公式を使いたいのですが、公式だけ使えればいいわけではありません。水面と出口でベルヌーイの定理を使う!
 管の中心のラインを基準とし、水面と出口でベルヌーイの式を使います。
管の中心のラインを基準とし、水面と出口でベルヌーイの式を使います。ベルヌーイの定理の使い方をマスターしよう!
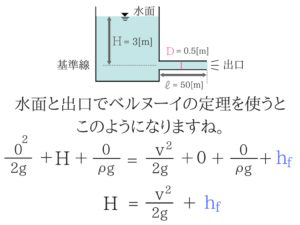
 このように速度水頭の項でくくるとわかりやすいでしょう。
このように速度水頭の項でくくるとわかりやすいでしょう。
サイホン ★☆☆☆☆
【水理学】⑦圧力計・流速計・流量計

解説は省かせていただきます。【水理学】⑧限界水深

比エネルギー ★★★★★
E-Q曲線とQ-H曲線 ★★★★☆
グラフの中の”どこが常流でどこが射流なのか”、”限界水深の時のEの値”などの特徴は勉強しておきましょう!限界水深を求める問題のポイント
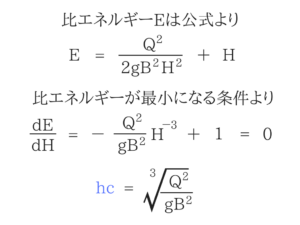
比エネルギーの式を水深Hで微分したものがゼロになるということです。
わからない人は答えを公式として覚えておきましょう! よくわからない人はこの答え「限界水深HC=」の形を公式として覚えてしまった方が早いと思います。
よくわからない人はこの答え「限界水深HC=」の形を公式として覚えてしまった方が早いと思います。限界水深を求める問題の解法

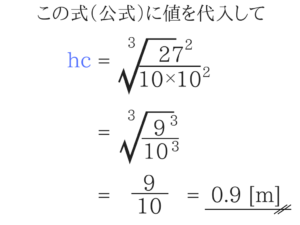 3乗根なので注意が必要ですね。
3乗根なので注意が必要ですね。
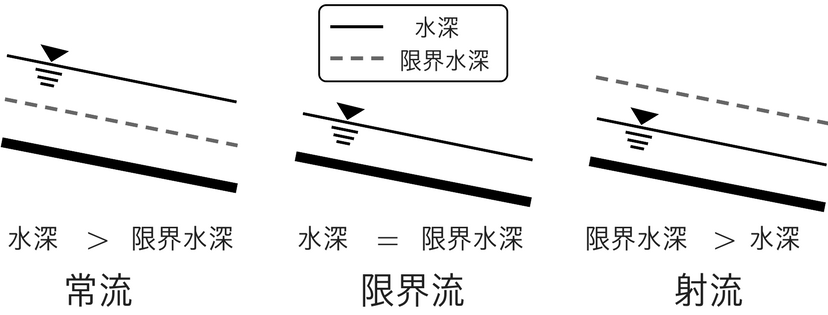
ルートの中で3乗を作れると消すことができます。常流と射流 ★★★★★
覚えることも単純なので確実にマスターしましょう!常流と射流のポイント
跳水 ★★★★☆
教科書に載っている常流や射流、フルード数との関係も覚えておきましょう!限界勾配と限界流 ★★★☆☆


【水理学】⑨相似則と無次元パラメーター

フルード数の公式と常流・射流・限界流との関係


最近もよく出題されているからね!
実際の問題も簡単そうだな~!【水理学】⑩水の粘性とせん断応力

【水理学】⑪オリフィス

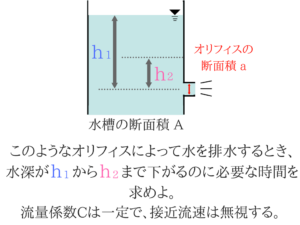
その中でも簡単な問題は解けるようにしておきたいですね。オリフィスの問題を解くポイント
(Cは流量係数、aはオリフィスの断面積)
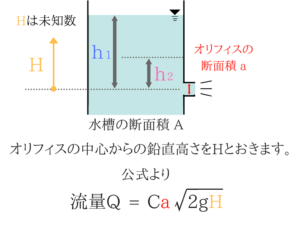
dQというのは流量の変化量、dHは水深の変化量など、”文字の意味をきちんと理解できているか”がポイントです!オリフィスの問題



dQ=面積×dH


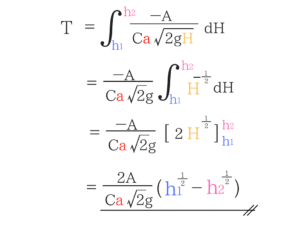
補足説明のところで書いた2式の使い方はそのまま覚えてしまってもいいかもしれません。

【水理学】⑫水の衝突力

水の衝突力のポイント

ポイントの補足説明

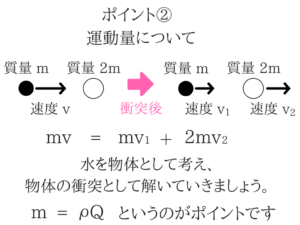
水の衝突力の基礎問題
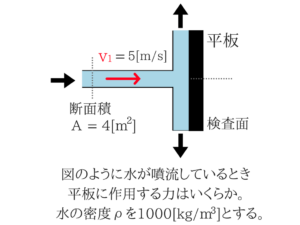
水の衝突力の公式は覚えておこう!
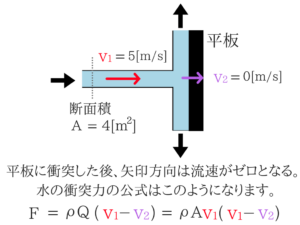
ちなみにここで連続の式Q=Avを使用しています。
mv1-mv2で余ったエネルギーが平板に作用する力となる、私はそんなイメージで解いていました。 少し難しいですが、基礎的な問題なので理解できるようにがんばりましょう!
少し難しいですが、基礎的な問題なので理解できるようにがんばりましょう!斜面への噴流の問題
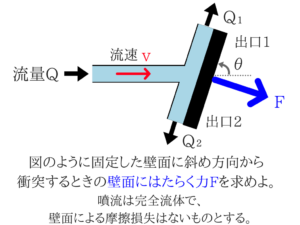
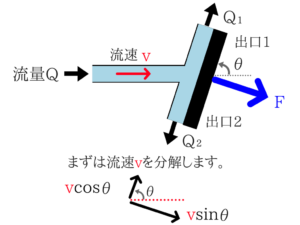
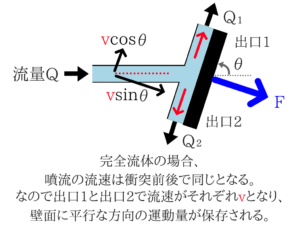


水の衝突力の問題も基礎的な部分はおさえるようにしておきたいですね。
お疲れさまでした!
実際に出題されている問題を解説しています↓
![公務員のライト[試験情報データベース]](https://senseikoumuin.com/wp-content/uploads/2022/12/cropped-logo-color-2.png)
















