【円運動と慣性力】エレベーターで体重計に乗ると…？謎の力についてはサラッと読んでおけばOK！

はっきり言って重要度低いです！
→物理の楽しさを紹介？

重要度は低いのですが、範囲が狭いですし、出題されるポイントも決まっているので
本番で出題されたときに得点しやすい分野となってます！

まぁ円運動は理解難易度が高めかなと思います。
→文系の方は捨て分野としてOK！

慣性力はイメージしやすく、理解難易度も低い！
→サラッと読んでおいて欲しい！

この分野について細かく解説しても仕方ないので
めちゃくちゃザックリ
重要なところだけ紹介していこうと思います！

主には公務員試験の物理対策として、
中学～高校の物理の分野すべてを解説していきますが、
もちろん中学生高校生の方が見ても参考になると思います！

ではさっそく【円運動と慣性力】分野の勉強をしていきましょう！

私は物理って言う科目がすごく好きなんですね。
今は公務員試験のせんせいとして、受験生の皆さんに物理が基礎となってる構造力学や水理学、土質力学なんかを教えています。
このページは『物理初心者の文系の方』に向けて書いたものです！

もちろん教養試験対策だけじゃなくて技術職の人の工学の基礎対策にもなると思います！
難しい話をしてもしょうがないから面白おかしく紹介していきますね！

【円運動と慣性力分野】初心者向けに４項目を解説！

この３つのテーマについて、基礎的な部分がわかるよう図でわかりやすく解説していきますね！

円運動と単振動については捨てテーマとしてOKですが
『慣性力』はイメージしやすく、難易度も高くないので
できればおさえておいてほしいなと思います！

では、本編にまいりましょう！

まずは「慣性力」から紹介します！
苦手な方はココだけ読んでおけばOK！

【慣性力】謎の力の正体とは…？サラッと読むだけでOK！

『慣性の法則』の項で基礎的な部分について紹介していますので、まずはそちらを見ていただくと理解しやすかもしれません。

実は日常生活の中でも「慣性力」に触れていることがあるんですね～！

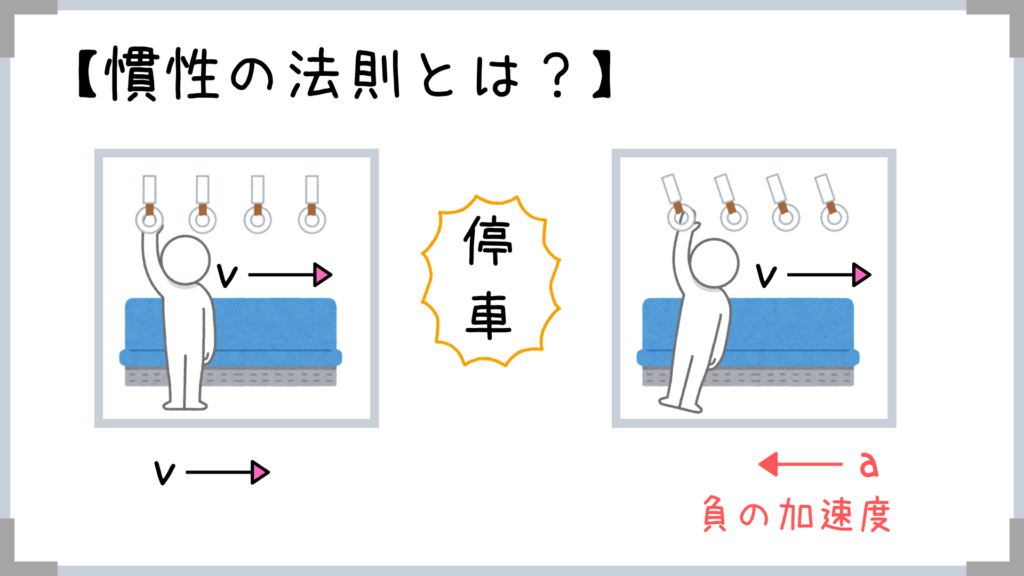
皆さんも電車に乗ってて、電車が止まる時に前向きに体が傾くことがあると思います。

この現象って「なぜ」だと思いますか～？

ちょっと『慣性の法則』を勉強した人ならこう答えると思います。

「電車と人は同じ速さで運動している。人は等速直線運動(前に運動)を続けようとしているのに、電車は止まるからバランスを崩した！」

その通りです！

急発進するときも同じですよね！
人間は静止し続けようとしているのに、電車は前に動いてしまうので後ろによろけるんです。

【慣性力】でも人間の視点からみてみると…

皆さんも新幹線に乗っていて駅で停車している時、反対方向から進んできた新幹線とすれ違って、どっちが運動しているかわからなくなることってないですか～？
「自分が前に進んでいると思ったら、新幹線とすれ違っただけだった」って意外にこういうことってあるんですよね。

何が言いたいのかというと、
人間の視点で見てみると
電車が走っているんじゃなくて周りの風景が動いているだけだと見ることが出来てしまうということです…(汗)

自分は静止していて、
周りの風景が動いている…！

自己中心的すぎる考え方ですよね(笑)

そして、このような視点で見てみると、不思議な現象が起きてしまいます。
外部から力がはたらかなければ静止している物体は静止し続けるハズ…！
誰かに押されたわけでもないのに体が傾いた…

→運動方程式が成り立たない!!

何だこの謎の力は…
そうです、この力が
慣性力です！
→慣性力を与えれば運動方程式を成り立たせることができる！

ちなみに、自己中の例のように運動方程式が成り立たない視点(目線)のことを「非慣性系」と言い
運動方程式が成り立たつ視点のことを「慣性系」と言います。

基礎知識はココで終わり！
こっから本題に入っていきます！

【慣性力の大きさ】加速度と反対方向に作用！

公式は「F=－ma」で、大きさ自体は「ma」です。
ｍ：質量、a：加速度

なぜマイナスがつくのかというと、
慣性力という力は
加速度と反対方向に作用するからです！

電車が右向きに急発進したとしたら
“後ろ”によろけるでしょ～？
電車は右向きに加速している
→左向きに力が加わる
→人は左向きによろける

まぁ結局問題が解ければそれでOKなので
さっそく１問解いていきましょう！

【慣性力の演習問題】特別区の過去問！

問題文がだらだらしていて読む気が失せるかもしれませんが、コイツは超簡単な問題ですよ！

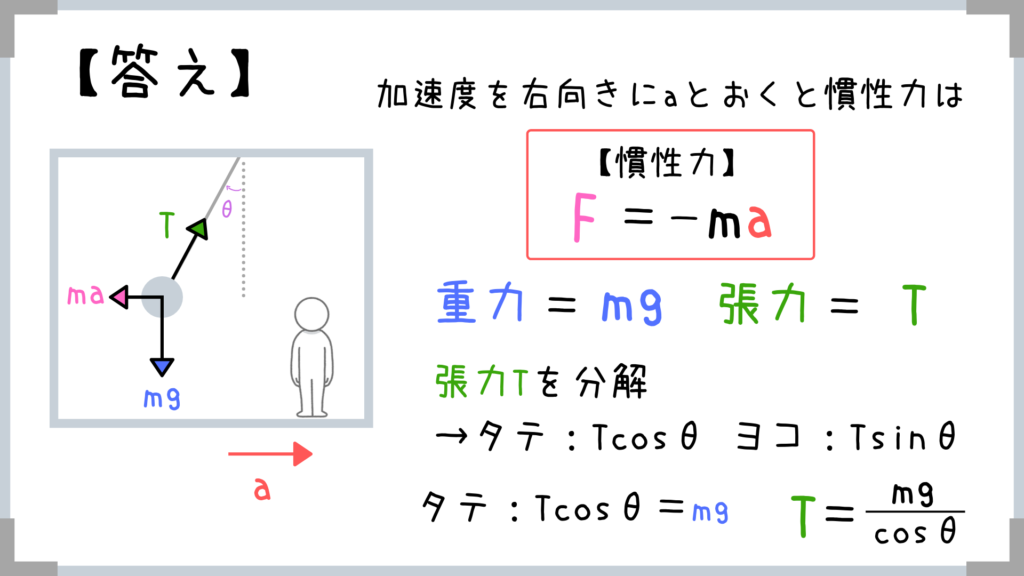Tとmaとmgはつり合い状態にあるので、三角形を作って三角比で求めてもOK！
ていうかこの問題簡単すぎますよね(汗)
慣性力とか関係なしに、力の分解をするだけで答えが出ちゃいます。

でもまぁ基礎問題としてはピッタリ。
今電車内の人の視点から見て、慣性力を利用して問題を解きましたが、
はたからこの電車を見て、運動方程式を使って解くことも出来ますよね！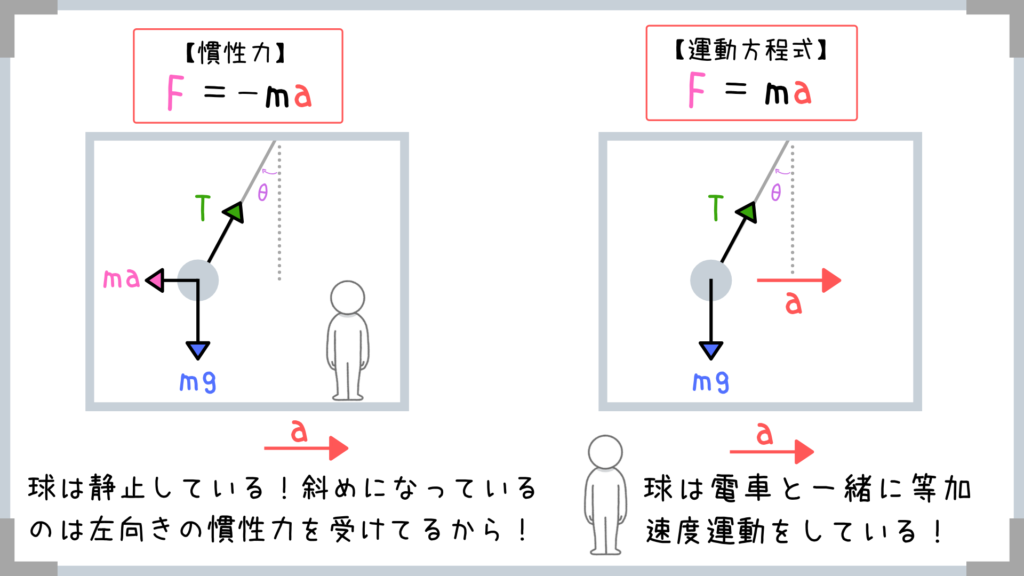

このように「慣性力を与えて静止した状態とみなす」ことと「客観的に見て運動方程式で解く」ことは等価であると言えます。

要は運動方程式を使うような問題が出たとしても、勝手に慣性力を与えて静止させた状態だと仮定してつり合いの式を立ててもOKということです。
(見方の違いだけということ）

【慣性力(おまけ)】エレベーターで体重を図ったらどうなるのか？

普通に体重計に乗って、
下にかがんだり、ジャンプしようとしたりすると
体重計の数値って変化しますよね！

体重は同じハズなのに、体重が増えたり減ったり…
コレは「慣性力」というみかけの力がはたらいているからなんですね！

「急にかがむ」という行為は「だるま落としの上のだるま」状態になるので一瞬フワッと浮くはずです。
→体重は軽くなる！(慣性力は加速度の反対方向に作用)

ということで…
エレベーターでコレとおんなじ原理を適用してみると
一瞬だけ体重を軽くすることが出来ちゃいます！

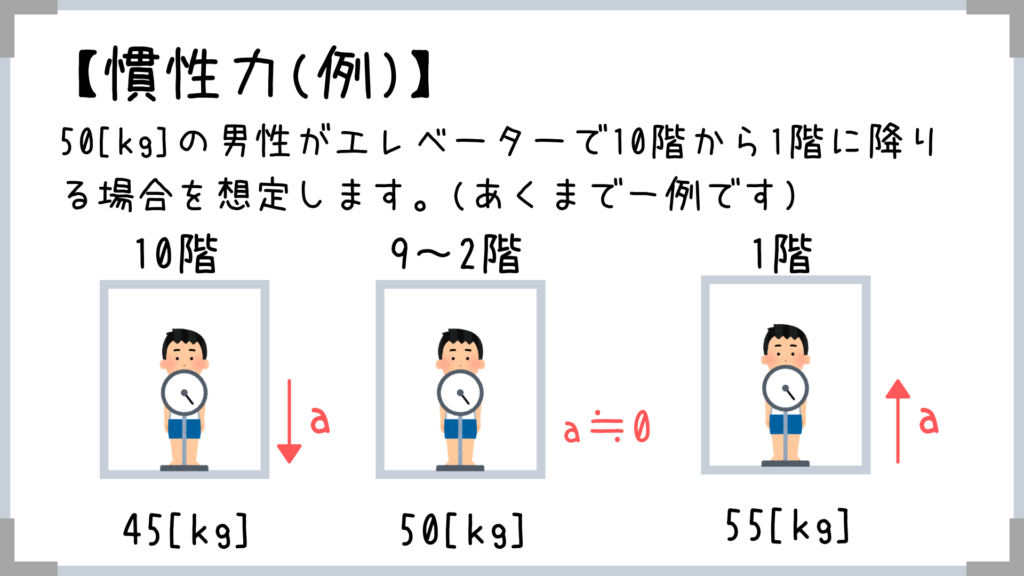
乗って降り始める瞬間は下向きに加速度aが発生します！
→上向きの慣性力がはたらいている！
→体重減

垂直抗力をNとして式を立てると
N+ma＝mg
→N＝m(g-a)

例えば重力加速度を10[m/s²]、下向きの加速度を1[m/s²]とすると
N＝50(10-1)＝450[N]となりますね！

逆に1階ではエレベーターは減速するため、マイナス方向に加速度が作用！
→下向きの慣性力がはたらいている！
→体重増

実はエレベーターというのは9~2階の部分は等速直線運動をしていて「加速はほとんどしてない」んですね！
→下向きの加速度の大きさは0.01~0.1[m/s₂]とか誤差レベル
→体重はほとんど変わらない

ダイエットしてて体重が減らない…と思っている方はこのようなチャレンジをすると
50[kg]の方なら±5[kg]くらいはイケると思いますので、一喜一憂できるかもしれませんね(笑)
(エレベーターの性能によっても変わってきます)

この分野は重要度低めになっています。
でも実際にこういうエレベーターの慣性力を使った問題も過去にでているのでみておきましょう！

【遠心力】文系の方は飛ばしてOK！(雑談)

遠心力というのも慣性力の１つなんですね！
車が急カーブした時体に「G」がかかると思います。
コイツも謎の力ですよね～！

とりあえず公式だけ覚えておけばOKかなというところです。
技術職志望の方についてはある程度重要になってきますので、「遠心力」については別ページで解説していきますね！

余談ですが、ハンマー投げってありますよね！
「遠心力でハンマーを遠くに飛ばす」ってたまに言っている方がいますが、厳密にいうとコレは間違っていると思います。

なぜかというと、ハンマー投げというのは「放物運動」だからです！
飛距離に起因するのは「初速度」と「角度」ですよね！
→遠心力というのは上の図で言うと右向きに作用しているので、もし遠心力でハンマーを飛ばすというならハンマーは右向きに飛んでいかなければいけません。
→上の図のタイミングで手を離すとvの速度の方向にハンマーが飛んでいくはずです。

とはいっても公式を見ていただいたらわかる通り
遠心力Fの値が大きくなるということは
必然的にvの値も大きくなるということです。
(mとrは基本的に一定ですからね！)

ということで「遠心力が大きくなるとハンマーは遠くに飛ばせる」という発言は間違いではありませんが、「遠心力でハンマーを遠くに飛ばす」というのは間違っている気がしますね。

ホントどうでもいい余談でした(汗)

ここは重要度が低い分野になっています。

【遠心力の演習問題】文系の方は飛ばしてOK！

ここらへんで真面目に１問だけ遠心力の基礎問題を解いておきましょうか！基本的に力を図示して、タテヨコのつり合いの式を立てて、求めたい値を求めていくっていう流れで解けばたいてい遠心力の問題は解けます！
(※めんどくさいんで最初に半径を求めちゃいました)

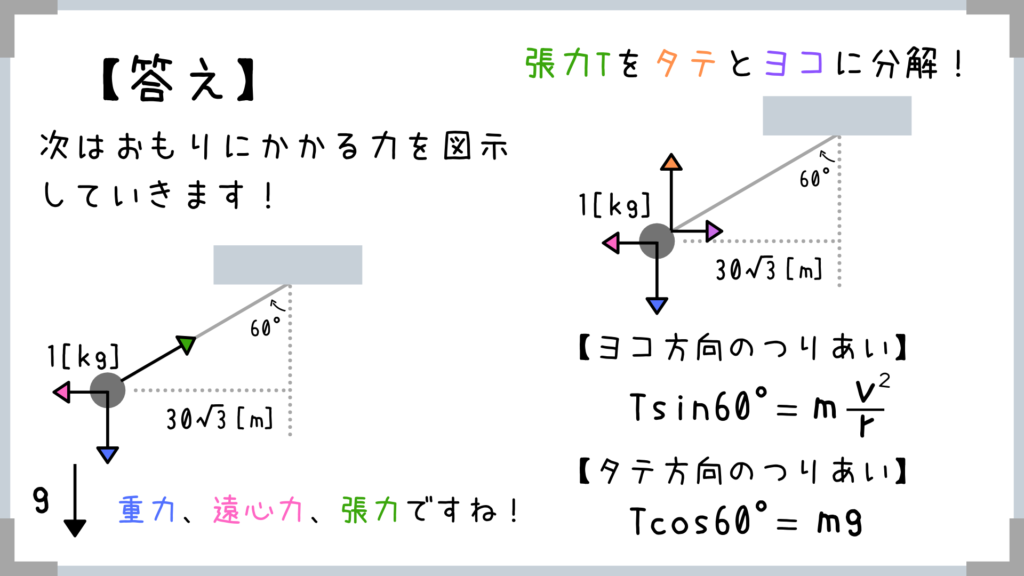力が図示できて、遠心力の公式を忘れずに書くことができたら、あとはタテヨコのつりあいの式を立てるだけ！

ちょっと難易度高いですかね？
ココまでの内容をきちんと理解出来た方なら余裕だったと思います！

【円運動】ココをきちんと理解しておくと、後でラク！

物体が円周上を一定の速さで運動する
→この運動を等速円運動といいます。

これから紹介していく「単振動」や「波動」について考えるときの基盤となるのが、この円運動の知識です。

これから円運動や単振動、波動系の問題を解くにあたって、必要な知識・公式がいくつかあるので
まずは基礎知識から紹介していきたいと思います！

大事なのは公式を丸暗記するんじゃなくて、公式の意味を勉強することだと私は思います！
やっていることなんて「速さ×時間＝距離」だけですからね！

【円運動の式①】物体の速度と角速度

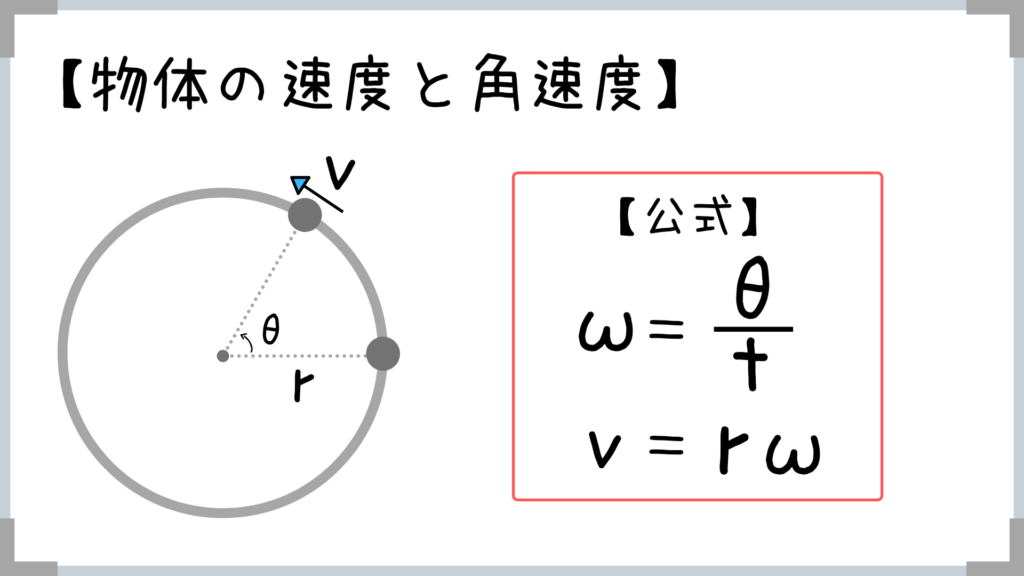角速度というのは、「１秒当たりに角度が何度進むか」ってことで、
t秒間で物体が角度θ[rad]だけ回転した時の角速度ωは「ω＝θ/ｔ」であらわせます。

単純に速さというのは「距離÷時間」ですよね！
それが「角度÷時間」になっただけです。

「ω(オメガ)」や「θ(シータ)」などの文字が出てくるので、少し複雑そうに見えますが、言っていることはめちゃくちゃ単純ですよね！

また、球の速度と角速度の関係式は「ｖ＝ｒω」となります。

高校物理では角度の単位として「弧度法[rad]」を使います。
まぁ難しいことは考えずに
「180°→π」って覚えておけばOK！

つまり「90°ならπ/2」「60°ならπ/3」「30°ならπ/6」ってことです！

【円運動の式②】周期と回転数

周期って言うのは、「１周して元の位置に戻ってくるまでの時間」のことです！

１周っていうのは360°のことなので、弧度法[rad]であらわすと「１周＝２π[rad]」となりますよね？
→これが角度というわけです。

角速度の単位はω[rad/s]…
→１秒当たりに角度がどれだけ進むか

ということで周期T[s]を式で表すと

T＝２π/ω

「ｖ＝ｒω」の関係式より
T＝２π/ω＝２πｒ/ｖ

「速さ×時間＝距離」じゃないですか？
→「角速度×時間＝角度」

時間(T)を算出したかったら「角度(２π)÷角速度(ω)」ですよね！
やっていることは超単純なんです。

そして、回転数って言うのは、単純に「１秒間に何周回れるのか」ってことです。

周期というのは、１周まわるのにT秒かかるってことです。
ということは
１秒当たり１/T周回れますよね！

１/T＝回転数！

公式が複雑そうに見えますが、意味を知ると簡単でしょ～？

例えば、１周まわるのに10秒かかる…ということは１秒当たり1/10周まわれるということですね！

【単振動】公式の形を覚えておくだけでも正答できる問題が出てます！

単振動…ぶっちゃけ重要度が低すぎる！
(力学の最終関門だと勝手に思ってます)

技術職志望の方はぼちぼち重要になってくるので、コレまた別ページで紹介していきたいと思います！

単振動を１から覚えようとするとあり得ない労力がかかりますし、明らかにコスパが悪いので基本的に文系の方は捨ててOK！

でも、公式の形と文字の考え方だけ覚えておくだけでも答えが出せちゃう問題が過去に何度か出ていますので、公式だけ知識として覚えておきましょう！

【ばね振り子と単振り子の周期】m、k、L、gを大小させる問題が出題されてます。

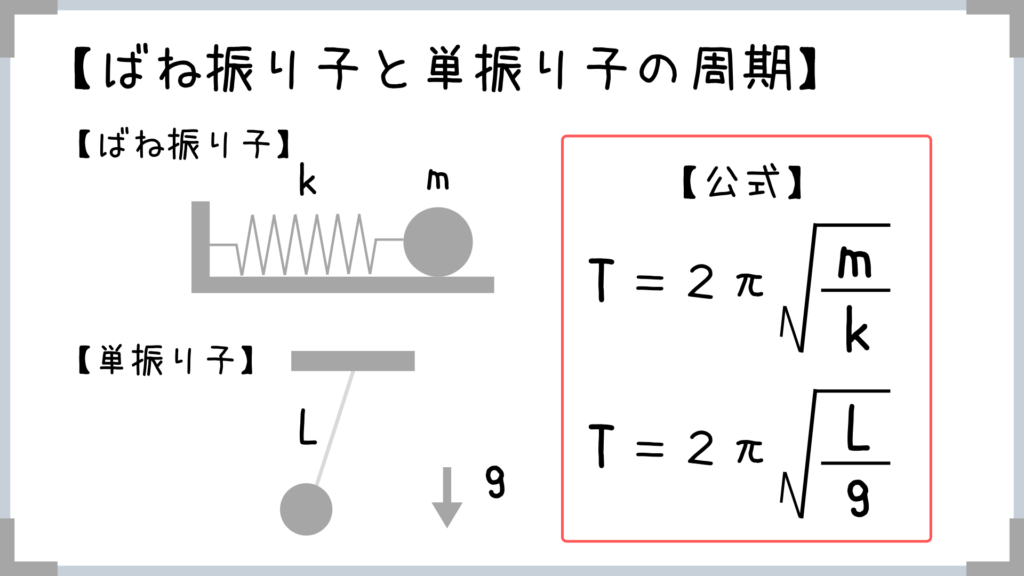
ばね振り子と単振り子の周期の公式はコレ！

実際はこの形だけ覚えておいて、mを大きくしたり、エレベーター等に乗せてgを大きくさせたり小さくさせたりして、周期Tの大きさの大小について考えさせる問題がよく出ています。
逆に文系の方はココだけおさえておけばOK！

技術職志望の方も単振動の問題が出たら、公式だけ知っていれば解けちゃう問題も過去に何回も出ています。

ということで公務員試験に出る【円運動と慣性力】の解説はココで終わり！

長々とお疲れ様でした！