【特別区】数的処理の出題数や過去問を紹介します！

こんにちは😊公務員のライトです！
Follow @koumuinright7

今回は、【特別区：数的処理】について、紹介していきます。

【特別区】数的処理の出題数

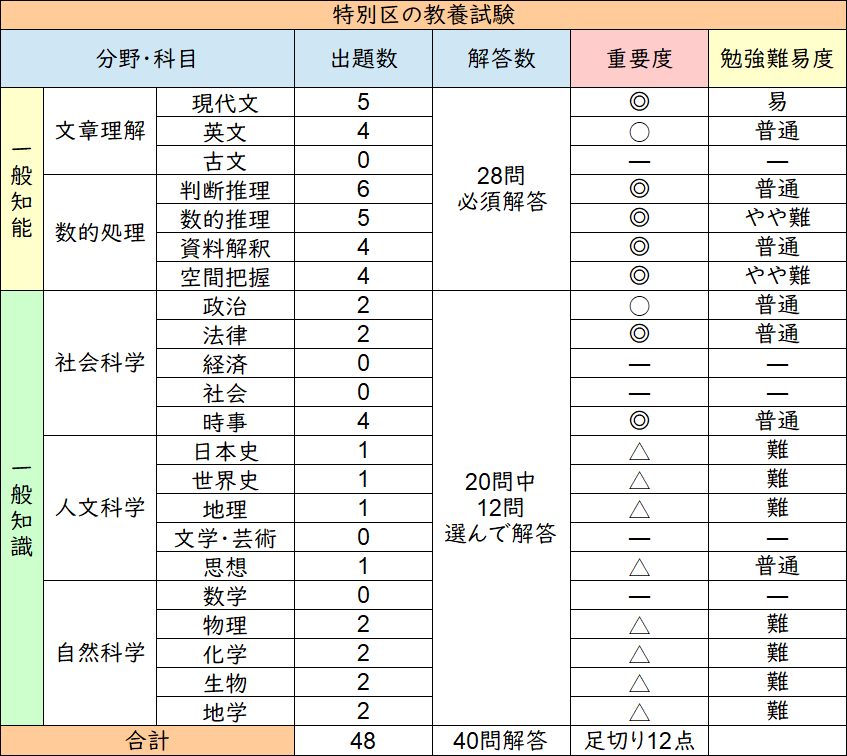
※重要度は「◎、〇、△、✕」の４段階、勉強難易度は「難、やや難、普通、やや易、易」の５段階です。

数的の出題数は計19問で、うち判断推理６問　数的推理５問　資料解釈４問　空間把握４問です。

特別区の数的処理は、最も多い科目です！

そもそも数的処理とは？

「数的処理」とは、筆記試験における教養択一試験の1分野です。 数学的・算術的な思考力・推理力を問う問題群であり、「判断推理」「数的推理」「資料解釈」「空間把握」の４つの分野に細分化されます。

【特別区】数的処理の出題形式

特に特別区試験は、判断推理の配点が多く、出題パターンもシンプルなので、得点源にしやすいです。

【特別区】数的処理の過去問を見てみよう！

【特別区】判断推理の過去の出題例

→答えは『４』です。

実際にこういった問題がでます。数学的知識は最小限で十分な科目ですが、上記のような暗号問題が直近の数年間で頻出となっていいます！そこで、１つの問題に深入りしないことが重要です！

【特別区】数的推理の過去の出題例

→答えは『３』です。

実際にこういった問題がでます。このように基礎的な問題が多く、国家系の問題と比べると簡単です。そこで公式を覚えることが大切です！

【特別区】資料解釈の過去の出題例

→答えは『５』です。

実際にこういった問題がでます。このように資料解釈の計算はたしかに大変なイメージが強く、後回しにされやすいのですが、概算などテクニックを習得するだけで、簡単に点数を取れるようになります！

【特別区】空間把握の過去の出題例

→答えは『3』です。

実際にこういった問題がでます。このように中高生のときに図形に苦手意識があった人にとっては、たしかに大変なイメージが強く、後回しにされやすいのですが、公式や裏技などテクニックを習得するだけで、簡単に点数を取れるようになります！

【数的処理の勉強方法まとめ】目指せ数的マスター！

【数的レベル１】

問題を見た時に「頭が真っ白」で全く解法が頭に浮かばないレベル

【数的レベル２】

問題を見た時に「なんとなく見たことあるけど、どうやって解くんだっけな？」ってあやふやなレベル

【数的レベル３】

問題を見た時に「多分この解法だろうな」って問題と向き合えるレベル

【数的レベル４】

問題を見た時に「このパターンの問題ね」って解法がパッと頭に浮かぶレベル

【数的レベル５】

問題を見た時に「これは落としてはいけない基礎問だ、こっちは捨て問だな」って瞬時に判断できるレベル！

どこに着目して、どのような知識を使って、どのように解くと楽に解けるのか、
これから数的処理を勉強する方に説明できるようになったらもう数的マスターです。

【特別区】数的処理の出題傾向

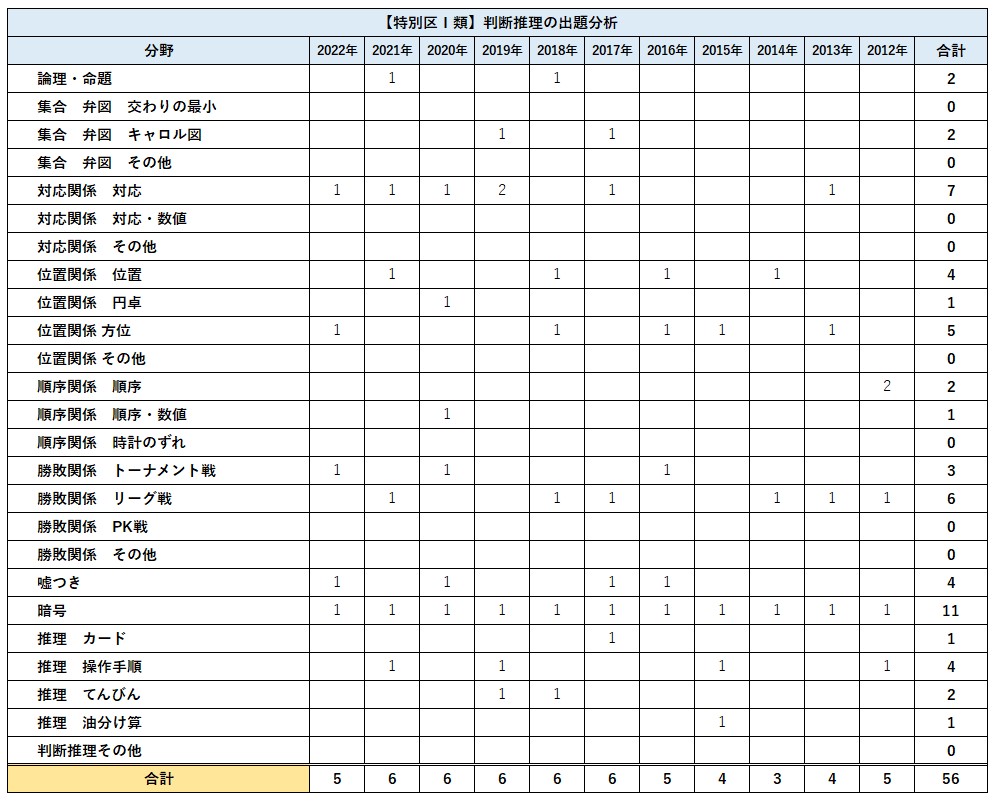
【特別区】①判断推理の出題傾向

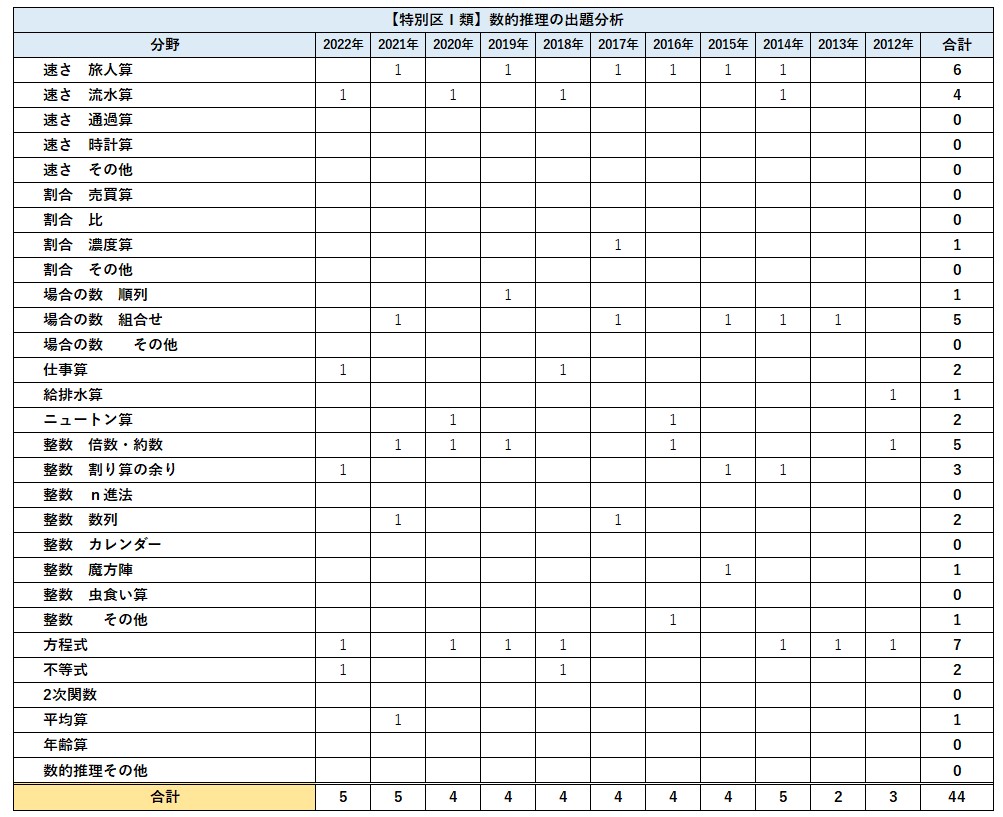
【特別区】②数的推理の出題傾向

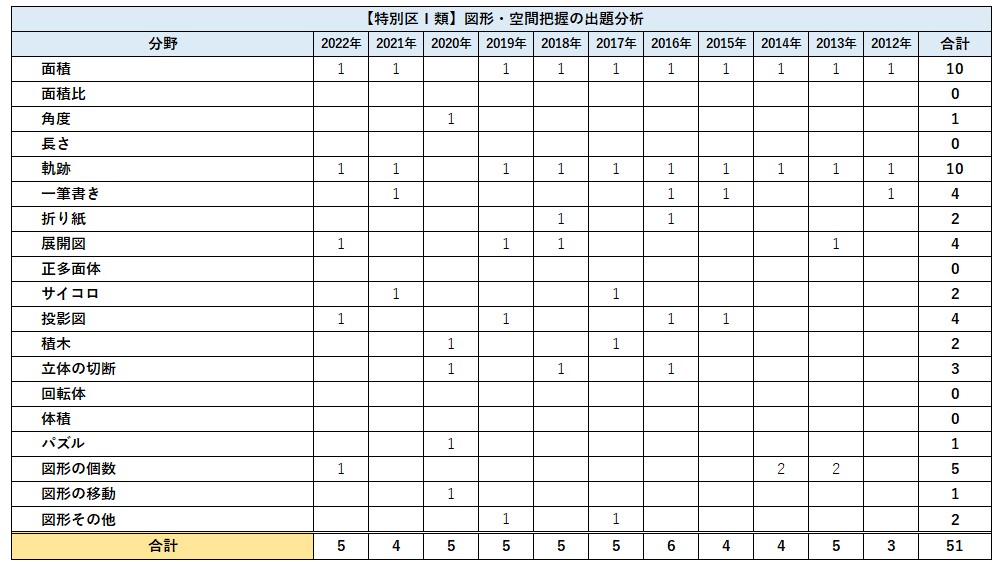
【特別区】③図形・空間把握の出題傾向

【特別区】④資料解釈の出題傾向

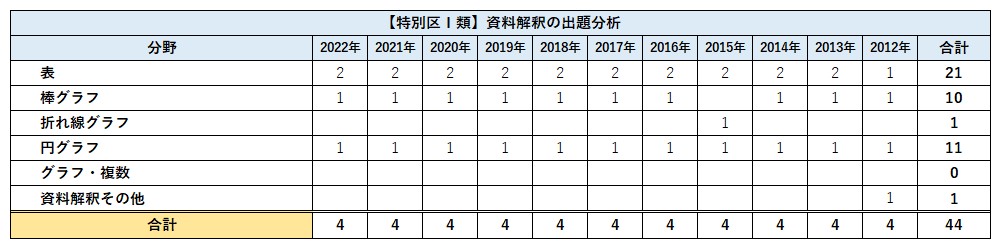
数的処理の出題数は19問です。内訳は判断推理から６問ほど、数的推理から５問ほど、資料解釈から必ず４問、図形をつかった問題が４問ほど出ます。出題数が多いので12以上は安定して得点をしたい科目です。単元としては勝敗関係と暗号、面積からそれぞれ１問必ず出題され、順序・対応・位置関係から２問ほど、速さから１問出題されることが多いです。2022年度はやや易化傾向にありました。全体の難易度としては国家一般職や国税と比較して少し易しいといえるでしょう。特に資料解釈は他試験でも頻出分野なので確実に得点できるようにしておきましょう。

【特別区】数的処理のオススメ講座

数的処理は苦手な方が多い科目ですが、全試験種で課される科目なので、克服したいと考えている人も多いのではないでしょうか？そこで、公務員のライトより、『たくまる数的講座』を発売しております✨ぜひご検討ください！

【特別区】数的処理対策まとめ

特別区を受験した受験生が実践したポイントをまとめてみました！

【特別区】数的処理の裏技勉強法を紹介！

数的処理が苦手な方はこちら

受講でお悩みの方は、お気軽にご相談ください。

講座に関する疑問や質問があれば、公務員のライトの受講相談ラインでお気軽にご相談ください😊

＼ 友達追加ボタン ／

この記事を書いた人【判断推理・数的推理・空間把握】

この記事を書いた人【資料解釈】