数的に拒絶反応が…
「判断推理」と「数的推理」は”重要度が高すぎる科目”です！
なんといっても公務員の教養試験ではこの2科目の出題数があり得ないくらい多いですからね～！
でもこの2科目、苦手な方がかなり多いんですよね。
とくに数的推理は数学的要素も強いため、苦手な受験生が多い印象があります。
そこで今回は「数的が苦手すぎて萎えている方」に向けて記事を書こうと思いました！
「苦手な方もうまく勉強して合格して欲しい」という想いで書いてます。
間違った勉強方法をしている方は、この機に改善して効率よく対策していってほしいなと思います！
では本編にまいりましょう！
目次
【数的処理が苦手】失敗しやすい人の特徴を紹介！
- 継続力が無い
- 考え方を間違えたまま継続
- 答えを暗記する(現実逃避)
- 目的と手段が混同してしまっている
- ネガティブすぎる！
- 人の言ったことをうのみにしてしまう
- 合格するビジョンが見えていない
あくまで私の個人的な感想ですが、↑このようなタイプの方は一度、自分の勉強方法や試験に対する考え方を見直してほしいなと思います。
それぞれ詳しく解説していきますね！
【数的処理の対策】①すぐに実力が身につく科目じゃない
数的処理という科目は新しい学問だと思ってください。
もちろん、中学受験の経験や数学の知識が役に立ったりするので、ゼロからのスタートではない人もいるかもしれませんが、基本的には皆同じようなラインからスタートすると思います。
実力がついてくるまでに時間がかかるのが数的処理という科目ですから、継続力は特に大事にしていただきたいなと思います。
数的の問題はいろんな解法がありますが、絶対に『早く解ける方法(解法)』が存在します。
最初は1問解くのにも時間がかかってしまうと思いますが、『どこに着目して、どういう思考で解いたら早く解けるのか』という思考を大事にしてみて下さい！
【数的処理の対策】②参考書を5周したのに新しい問題が解けない
私に相談してくれる方って公務員になりたいという想いは強いので、ほとんどの方がたくさん勉強しているんですよね！
絶対にどこかに原因がある！
継続力はあるけど、できるようにならない…
ということは歯車が狂ってしまっている原因がどこかにハズです！
→この原因を探っていきましょう！
考え方を間違えたまま勉強してない？
このような方は間違った考え方・勉強方法をしてしまっている可能性があります。
勉強方法や数的処理という科目に対する考え方が間違ってしまっているまま勉強を続けても、『無駄な時間』を過ごしてしまう可能性が高いですからね！
とくにこの手の方は1問解くのに1時間も2時間もかけてしまっている方が多いように感じます。
そんなに時間を使っていたら効率が悪いですし、他の科目にも悪影響を及ぼしてしまいますので、今から原因を見つけていきますよ！
【数的処理の対策】③勉強した気になってない？
「参考書を何周もまわせ」ってよく言いますよね！
もちろん参考書の問題を繰り返し解くというのはめちゃくちゃ大事なんですが、ただ繰り返せばいいというわけではありません。
作業は時間の無駄！
究極な話、参考書を100周して同じ問題を解いて…ってやってたら、
そのうち『作業』になってしまいますよね？
どうでしょうか、皆さんは作業になってしまっていませんか？
問題解いて…解法をノートに写して…って
これじゃあ時間の無駄もいいとこですよね！
→参考書を解く目的が理解できてない！
答えを暗記してない？
また、『答えを暗記してしまっている』っていうのも危険なパターンの１つです。
答えを暗記するほど参考書を何周もして頑張っている受験生がいました。
この受験生は真面目に勉強しているのですが、答えを暗記してしまっているのでスラスラ解けてしまいます。
⇒コレで自分ができた気になってしまっているんですね！
もちろん、その問題の解法をマスターしたのは素晴らしいことですが、自分が解ける問題を何回も何回も繰り返し解いても意味がないですよね！
答えの暗記は現実逃避
無意識のうちに行っている『現実逃避』の一つだと思います。
→その参考書は一旦用済み！新しい問題に挑戦するべき！
何のために参考書をまわしているのかって部分を大事にしてほしいです。
【数的処理の対策】④なんのために参考書を使うのか理解できてる？
一旦、参考書を使う理由という点について考えてみてほしいなと思います。
最終目標は合格
まず最終目的は公務員試験に合格するためだと思います。
変な話、数的処理ができなくても公務員試験に合格できるなら問題ないわけですよね！
合格するために数的を捨てるわけにはいかない
でも基本的に出題数の４割前後を占めているのが数的処理という科目なので、ココできちんと得点できないと合格できる可能性がどんどん低くなってしまうわけです。
本番の試験で自力で得点するために勉強する！
当然、目的は参考書で得点することじゃありませんよね！
本番の試験で、自分の力だけで問題を解いて得点しなければいけないわけです！
⇒だから参考書使って基礎知識を身に着けたり、模試を受けて実力試しをしたりするわけですよね！
一旦、目的と手段を整理してみよう！
失敗しやすい人はこの『目的と手段』の部分がこんがらがってしまっている方が多いように感じました！
- 最終目的：公務員試験に合格したい
- 目的：本番の試験で合格点を取らなきゃいけない
- 手段１：そのために参考書を使って勉強する
- 手段２：模試を受けて実力をためす
私はきっと当たり前のことしか言っていないと思いますが、
参考書を解くことが目的になってしまっている人が意外に多いんですよね～！
どれだけ参考書の問題が解けたところで本番の問題が解けなければ意味がありません！
【数的処理の対策】⑤失敗したら萎えて終わり？
④の目的と手段の話と似ていますが、Twitterで紹介したものをUPしたいと思います。
とある受験生から相談されたものですが、重要なのでシェアしますね！
模試や参考書は何のためにある？
模試の例ですが、参考書でも同じ話です。
何がダメだったかを見つけて改善していこう！
参考書の問題が自力で解けなかったということは、どこかに『反省点・改善点』があるハズですよね！
「次は自力で解くために問題文のどの点に着目すれば良いのか」「どんな知識が必要だったのか」など、こういった部分をきちんと振り返って次に生かそうと努力できる人間は数的処理もどんどんできるようになっていく傾向にあります。
【数的処理の対策】⑥自分にあった参考書があるハズ！
数的処理という科目を対策するためには参考書が必要ですが、「講師はあくまでもアドバイザー」だということを意識して欲しいなと思います。
自分に合う参考書はホントにそれ？
講師や先輩等、他の方が良いよって言った本も当然いい本だと思いますが、基本的に大衆向けです！
たしかに、その本をマスターすれば公務員試験に合格できるようになるかもしれませんが、その本ってホントに自分にあっていますかね？
自分のレベルにあった参考書があるはず！
変な話、算数が理解できていない人がいきなり高校レベルの数学の問題を解いても理解に苦しみますよね？
→自分のレベルにあった参考書を自分で選ぶべき！
参考書は”自分で”選ぼう！
私もオススメの参考書を紹介していますが、コレは大衆向けであって、その人個人にあった参考書ではありません。
例えば、100人に同じ参考書をオススメしたとして、95人は合うかもしれないですけど、5人はあわないと思うかもしれないってことです。
ココはもう自分で判断するしかありませんよね？
直接目で見て判断しよう！
本屋に直接足を運んで、
「この本やさしく解説してくれててわかりやすいな」
「レベル的にも私にピッタリだな」
「文字や見た目が良くてやる気出そうだな」
って自分に合う参考書を
自分で考えて選んでほしいなと思います！
数的処理という科目は公務員試験合格に大きく影響してくる重要科目ですから、自分に合った参考書で効率よく対策していきましょう！
【数的処理の対策】⑦数的を捨て科目にしてOK？
そもそも公務員試験というのは満点を取る試験ではないですから、
皆が取れる問題を自分も落とさないようにするって考えが非常に大事です。
問題難易度は問題ごとに全然違う！
過去問を見たらわかると思いますが、数的の問題の難易度も問題ごとに全然違います。
基礎的な知識だけあれば解ける問題もあれば、10人中1人くらいしかまともに解けないような難問もあります。
皆が取れる問題は落としてはいけない！
どんなに苦手だと言っても最低5割、できれば6割くらいは取りたいところです。
これを目標にしましょう！
テーマごとにも難易度は違う！
数的処理が苦手でどうしても得点できる気がしない
こんな方は戦略次第で苦手なテーマを捨てることも可能だと思います。
合格ボーダー点はだいたい決まっている
合格ラインってだいたい6割前後だと思います。
⇒ということは教養試験全体で6割取れればいいわけですよね！
苦手分野・苦手科目は他でフォローしてもいい！
要は満点を取る必要はないわけですし、教養全体で得点できればいいわけですから
数的が苦手なら、他の科目でフォローすればいいって考え方もできますよね？
もちろん数的全部捨てたら大打撃なのでヤバいですけけど、頻出テーマだけは頑張って基礎部分だけおさえて、空間把握やはやさの問題など、苦手な部分は捨てて…ってうまく向き合っていくことはできると思います！
自分なりの得点戦略を！
このように教養科目の出題数と、自分の目標点についてきちんと考えて、戦略的に本番に挑んでほしいなと思います。
基本的には苦手なテーマでも、『基礎的な問題だけは落とさない』って考え方が大事です。
【数的処理の勉強方法】正しい考え方で対策しよう！
これから私が正しいと思う数的処理の勉強方法について紹介していきます！
- まずは解き方・解法を覚える
- 参考書を回して解き方になれる
- 新しい問題に挑戦してみる
- 復習！反省点・改善点についてきちんと振り返る
勉強方法に関しても細かく解説していきたいと思います！
【数的処理の勉強方法】STEP１：まずは解き方・解法を覚える
まずは解法パターンを覚えるために参考書を使います。
どの参考書にも「基礎問題」があると思いますので、この問題の考え方・目の付け所を勉強していきましょう！
この手の問題はどういう思考で解くと楽に解けるのかという部分を意識して問題に取り組んでみて下さい！
とりあえず参考書1周するという考え方も大事！
雰囲気を掴むために「とりあえず１周する」って考え方も大事だと思います。
→１周目からすべて完璧に覚えろっていうのはちょっと無理がありますからね！
問題内容や雰囲気を把握しよう！
「条件の整理の仕方」「表の作り方」「どの条件がキーとなっているのか」「どんな知識(公式)が必要なのか」ってとりあえず雰囲気をつかんでください。
→最初はすぐに答えを見てもOKです！
解説がわかりにくかったら他を探してみよう！
もしこの段階で解説が理解しにくいなって思ったら、その参考書は自分にあっていない可能性があります！
→本屋に行って他の参考書を立ち読みしてみましょう！
【数的処理の勉強方法】STEP２：参考書を回して解き方になれる
１周まわしてみるとなんとな～く解法が頭に浮かぶようになってきているハズです。
→実力で解けなくても、答えを見て「あ～そういえばこんな解法だったなぁ」って思うはずです。
→今度は答えに頼らずに自力で問題に向き合ってみて下さい！
自力で問題を解きたい！
本番では自分の実力だけで問題を解かなければいけませんから、問題を見た時に完璧に解法が頭に浮かぶ(第一目標)ようにしたいわけですよね！
このレベルに到達できるまで参考書を最低何周か回して、問題を繰り返し解いていくってわけです！
先ほども言ったように、簡単に実力が見に付く科目ではないですからね！
解法が頭に浮かぶまでに3~5周する人が多い
ちなみに、この第一目標である「問題を見た時に完璧に解法が頭に浮かぶ」っていうレベルに到達するまでに参考書を３～５周繰り返すって人が多いです。
→世間的に言われている「３～５周回せ」っていうのはこのレベルのことですよね！
問題点や反省点は絶対に出てくる！
でも参考書の問題を繰り返し解いていると、
１周目解けた問題が２周目は解けなかった…
この問題を解くのは３回目なのに解法が頭に浮かばない…などと
何かしら問題点が出てくると思うんですよね。
問題点との向き合い方が大事！
この問題点への向き合い方が大事だと私は思います。
「どういう考え方が必要だったのか」
「どこに着目すればよかったのか」
「どのように条件を整理すれば答えを導けたのか」
って反省点を大事にしてほしい！
『どういう思考で解けば自力で解けたのか』を大事に！
『なぜ』解けなかったのか
次自力で解くためには『どうすればいいのか』という点を意識して、頭を使って参考書の問題に取り組むようにしましょう！
難易度が高すぎる問題は飛ばしてもOK！
ちなみに、チャレンジ問題や発展問題などの難易度の高い問題はすべて飛ばしてOKです！
このレベルに到達することが出来たら次はSTEP３ですね！
【数的処理の勉強方法】STEP３：新しい問題に挑戦してみる
できる人と苦手な人との差はココだと思います。
参考書を繰り返し解いたことで、数的・判断推理という科目に対する耐性が身についていると思うんですよね。
ようやく本物の敵と戦えるレベルに到達できたってことです！
どんどん新しい問題に挑戦してみよう！！
実際に新しい問題に挑戦してみて、それが自力で解けるようであれば自分の実力が確かなものであるということです。
その指標になるのが『実際の過去問』や『模擬試験』というわけですよね！
アウトプットを大事に！
過去問や模試の問題は、本番レベルの問題ですから、こいつらと戦えるようになったのなら合格レベルだということです。
解けないところはきちんと反省！
もし解けないようなら、もう一度参考書を見て「自分には何か足りなかったのか」きちんと復習する必要がありますよね！
6割取れたら合格レベル！目標は7割でいこう！
今のうちに１つ注意点を話しておきますが、先ほども言ったように
公務員試験というのは満点を取る試験ではないですよね！
当然、数的処理という科目でも満点目指す必要はありません。
→6割取れたら合格レベルでしょう。
解く必要のない難しすぎる問題は飛ばしてOK！
実際の過去問や模擬試験の問題って『解く必要のない問題』も含まれているんですよね！
どういうことかというと、
難易度が異常に高い、正答率の低い問題ですね！
この手の問題は他の受験生も解けないわけですよ。
こういった問題は解く必要もありませんし、復習する必要もありません。
(※参考書、過去問、模擬試験すべてにおいて言える話です)
難易度の判断ができるようになれば数的マスター！
この『解く必要のない問題』を取捨選択できるようになったら、もうあなたは数的マスターですよ！
数的マスターが最終到達地点だと思います。
→このレベルまで頑張って演習して欲しい！
【数的処理の勉強方法】STEP４：復習！反省点・改善点についてきちんと振り返る
参考書を使ってパターンごとの解法をマスターできたどんどん新しい問題に挑戦してください！
新しい問題に挑戦
→復習・反省
→また新しい問題に挑戦
→復習・反省…
ってコレを繰り返しおこなっていけば、間違いなく数的処理の実力は合格レベルに到達すると思います。
→この復習と反省という部分が一番大事です！
何のために模試を受けているんだい？
模試を受けて、復習もせずに受けたまま…
解けなくて萎えて「もう知らない…」ってなってしまう方は注意が必要ですよ～！
→自分の中の課題ときちんと向き合う姿勢が大事だと思います！
本番の問題が解けるまでの勉強量は人によって違う！
また、不安要素の１つとして、このレベルに到達するまでの時間って言うのがあると思います。
努力が結果に結びつくまでの時間って人それぞれですからね！
努力不足だけは避けたい！
でも数的が得意な人ですら当たり前のように参考書を５周以上解き、色々な試験の過去問に挑戦して復習して、模試を何度も受けて復習して…ってしてますから
いつまでたってもできないという方は単純に「努力不足」だと思ってしまいます。
もしくはこの記事でも紹介したように「勉強方法(努力の仕方)が間違ってしまっている方」ですよね。
本番では過去問レベルの問題を自力で解かなければいけない。
実際に自分は解けなかった
「じゃあ次自分が自力で解くためにはどうすればいいのか」って考えて日々勉強に取り組んでほしいなとおもいます(^o^)/
【数的処理の勉強方法まとめ】目指せ数的マスター！
- まずは解き方・解法を覚える
- 参考書を回して解き方になれる
- 新しい問題に挑戦してみる
- 復習！反省点・改善点についてきちんと振り返る
この４つの手順を大事に、数的マスター(数的レベル５)を目指して欲しいなと思います！
【数的レベル１】
問題を見た時に「頭が真っ白」で全く解法が頭に浮かばないレベル
【数的レベル２】
問題を見た時に「なんとなく見たことあるけど、どうやって解くんだっけな？」ってあやふやなレベル
【数的レベル３】
問題を見た時に「多分この解法だろうな」って問題と向き合えるレベル
【数的レベル４】
問題を見た時に「このパターンの問題ね」って解法がパッと頭に浮かぶレベル
【数的レベル５】
問題を見た時に「これは落としてはいけない基礎問だ、こっちは捨て問だな」って瞬時に判断できるレベル！
どこに着目して、どのような知識を使って、どのように解くと楽に解けるのか、
これから数的処理を勉強する方に説明できるようになったらもう数的マスターです！
自分が合格レベルの能力を持っていると、「私が解けないと判断した問題なら他の受験生も解けないだろうな」って余裕で捨て問を判断できるようになると思います。
ココまで到達したら真の数的マスターですね！
【判断推理の頻出テーマ】受験先ごとにまとめました！
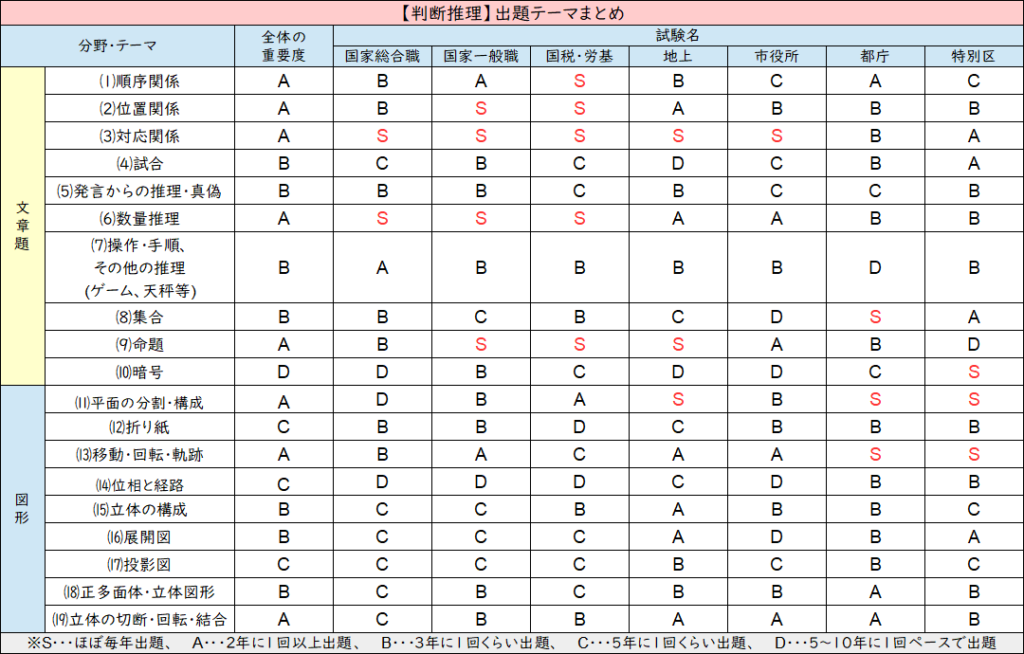
判断推理の頻出テーマについてザックリ紹介すると↑こんな感じ。
コスパやおすすめ度ではなく、
出題頻度の紹介なので
この点には注意してくださいね！
色々な試験を併願するなら、
基本的にはすべての単元をまんべんなく勉強しておいて、
試験直前期に頻出テーマを重点的に対策するっていう勉強スタイルがいいんじゃないかなと思います。
【数的推理の頻出テーマ】受験先ごとにまとめました！
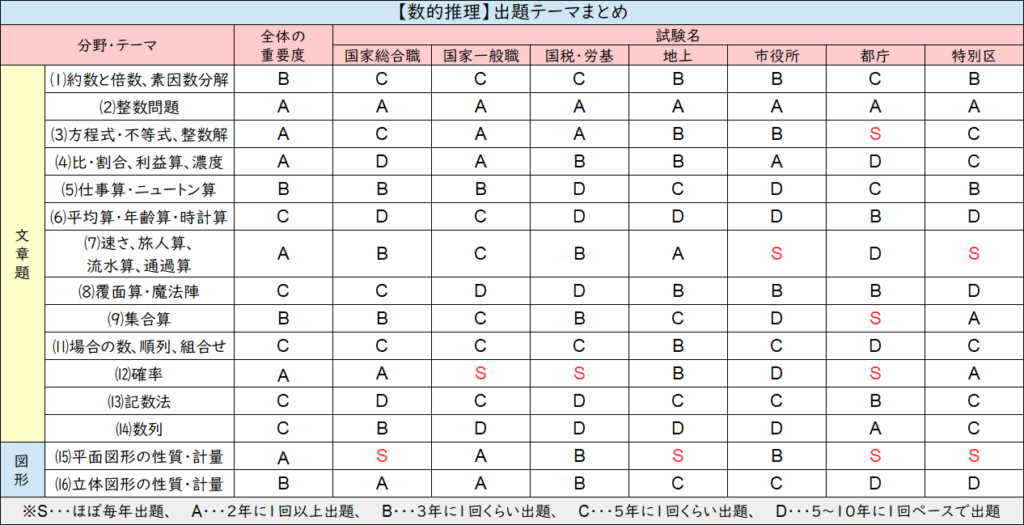
数的推理の頻出テーマについてザックリ紹介すると↑こんな感じ。
こちらもコスパやおすすめ度ではなく、
出題頻度の紹介なので
この点には注意してくださいね！
数的処理は特に苦手な方が多いので、
頻出テーマとそうでないテーマとの向き合い方というのが大切になってきますよね！
苦手な方も基本的に「みんなが落とさない問題を落とさない」って考え方が大事になってくるので、頻出テーマもそうでないテーマも「基本的な問題」だけは解けるように準備しておいてほしいなと思います！
まぁでも苦手すぎて拒絶反応を示してしまっている方は、受験先ごとの頻出テーマや出題傾向を参考にして、テーマをうまく絞っていってほしいなと思います。
【受験先ごと】数的処理の出題傾向・特徴についてまとめました！
これから数的推理・判断推理という科目をそれぞれ分野・テーマごとに分けて
受験先ごとに出題傾向・特徴の紹介を行っていきたいと思いますが
あくまで私の個人的な見解なので
参考程度に見ていただければと思います。
今回はこの６区分にわけて考察していきたいと思います！
先ほども言いましたが、おすすめ度やコスパではなく、ただの『出題頻度』なので、その点気を付けて下さい！
例えば、Cというテーマでも３年に１回くらいは出題されているので、きちんと勉強しておかなければいけませんよね！
つまり基本的にはすべての単元をまんべんなく勉強すればいいということです！
【国家総合職】数的・判断推理の出題テーマ＆特徴
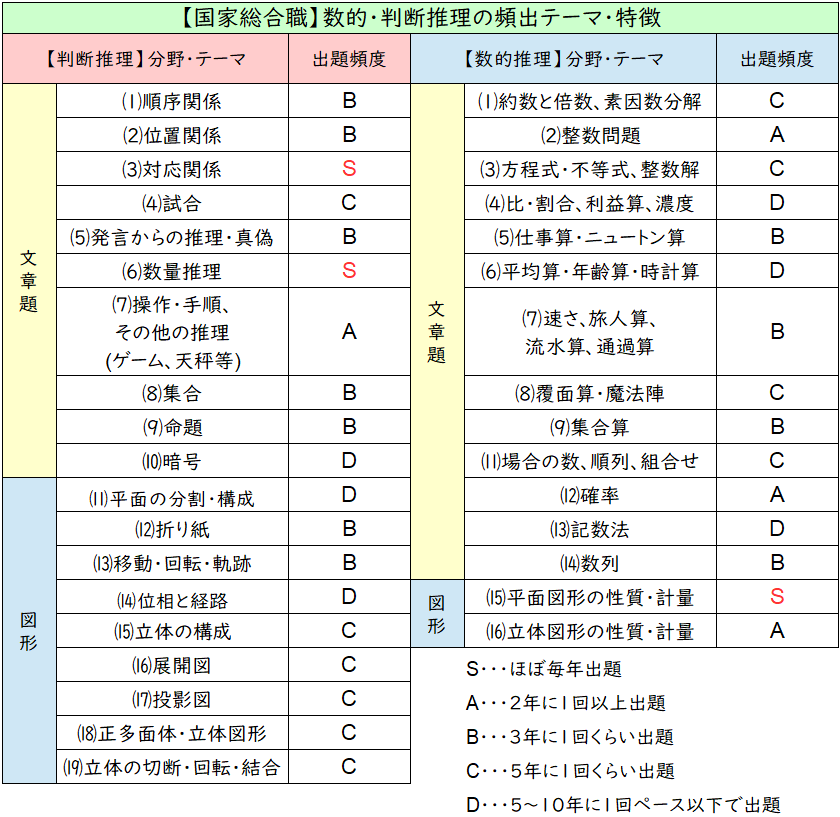
国家総合職の問題は文章が長いものが多いのが特徴かなと思います。
複雑な文章からいかにうまく条件を整理できるかってところが重要になってくると思います。
(1)~(3)が重要なのはもちろんのこと、他の試験に比べて(6)~(7)の「数量推理」や「操作・手順」の出題頻度が高いように感じます。
また、「集合」と「命題」を論理としてひとくくりにすると、２年に１回以上は出題されていますので、対策必須ですね！
数的系の文章題も幅広いテーマから出題されていますが、中でも「(12)確率」や「(2)整数問題」「(5)仕事算・ニュートン算」などが少し多めかなといった印象。
また、判断の図形に関しては、「(13)軌跡」や「(12)折り紙」の問題が出やすいのかなといった印象はありますが、その他のテーマも３年に１度くらいは出題されているので、絞って対策するのはNGだと思います。
数的の図形に関しては(15)~(16)の三角形や円の性質・面積や立体の性質・面積・体積などの出題が多く、毎年１問は出題されている頻出テーマとなります。
【国家一般職】数的・判断推理の出題テーマ＆特徴
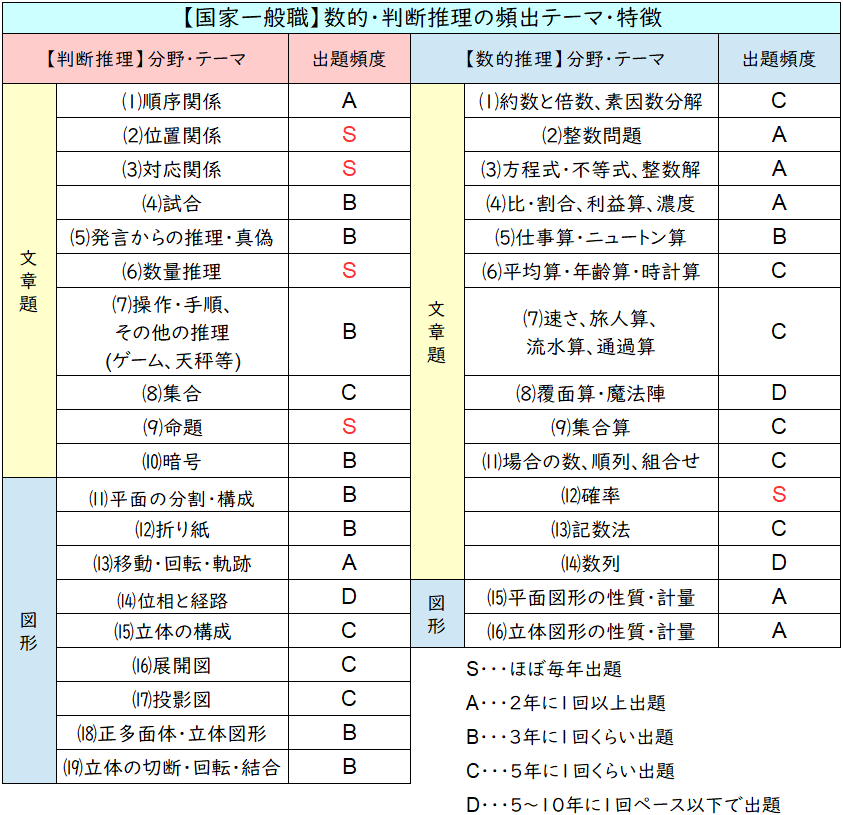
なんてったって国家系の試験は数的処理の出題数が多いですから、きちんと対策していきたいですよね！
受験先ごとの出題科目の紹介をするにあたって
国家一般職の出題数を基準に色々考察していきたいと思います。
【判断の文章】
なんといっても(1)~(5)の文章条件からの推理系の問題は毎年４～５問出題されている鉄板分野です！
また、(6)~(7)の数量条件から推理系の問題も毎年１～２問は出題されているような感じですね！
(8)~(9)の論理形式の問題も近年は毎年１問出題されています。
このあたりのテーマはガッツリ対策していきたいところですね！
【判断の図形】
毎年１～２問出題！
近年幅広く出題されていますが、問題の難易度の緩急が激しいです。
基礎的な問題は落とさないってイメージで、対策も基礎的な問題を幅広く行っていきたいですね！
一応、近年の傾向でいうと「(11)平面図形の分割・構成」「(13)軌跡」「(18)正多面体」が多いのかなといった印象。
【数的の文章】
毎年３～４問出題！
「(12)確率」「(4)比・割合」の問題が多いように感じます！
他にも「(5)仕事算」や「(3)整数解」など幅広いテーマから出題されていますが、記数法や覆面算・魔法陣、数列などの頻出が低いテーマもあります。
【数的の図形】
毎年１～２問出題！
(15)三角形や円の性質・面積などの問題が目立ちます！
難易度の緩急は激しいです！
頻出テーマこそあるものの、全体的に見ても幅広く出題されているのでやっぱり数的処理という科目はガッツリ対策していきたいですね！
まぁでも満点を取るのは超難しい科目なので、
他の皆が取れる正答率50％以上の問題は落とさないようにするのが目標かなと思います！
【国税・労基】数的・判断推理の出題テーマ＆特徴
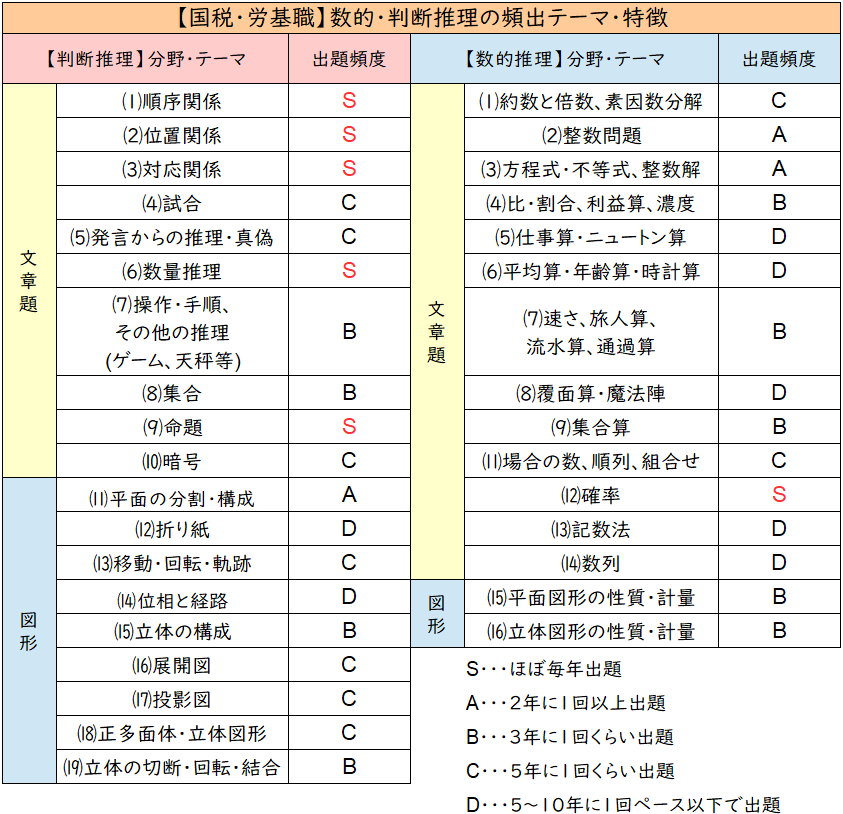
国税・労基も国家一般職とほとんど傾向は同じように(1)~(7)の文章・数量条件からの推理系の問題が多いのが特徴！
→毎年５問前後出題されている
「(9)命題」「(12)確率」も頻出で毎年ほぼ１問出題されている。
→令和元年度は確率の出題ナシ
これ以外にも「(3)整数解」「(5)比・割合」「(7)速さ」が頻出しているので、これらの頻出テーマだけおさえておいても本番である程度戦えると思います。
→出題頻度が「D」のテーマは無理に勉強しなくてもいいんじゃないかなと思います。
図形関係の問題については、分野としての出題はありますが、ココが頻出というテーマはないので、幅広く対策しておく必要があると思います。
あと、国税・労基の問題は難易度が若干高すぎる問題や捨て問も目立つので、この点に注意！
→きちんとした実力を付けて本番に挑む必要がある！
→問題を取捨選択できる判別力も大事！
【地方上級】数的・判断推理の出題テーマ＆特徴
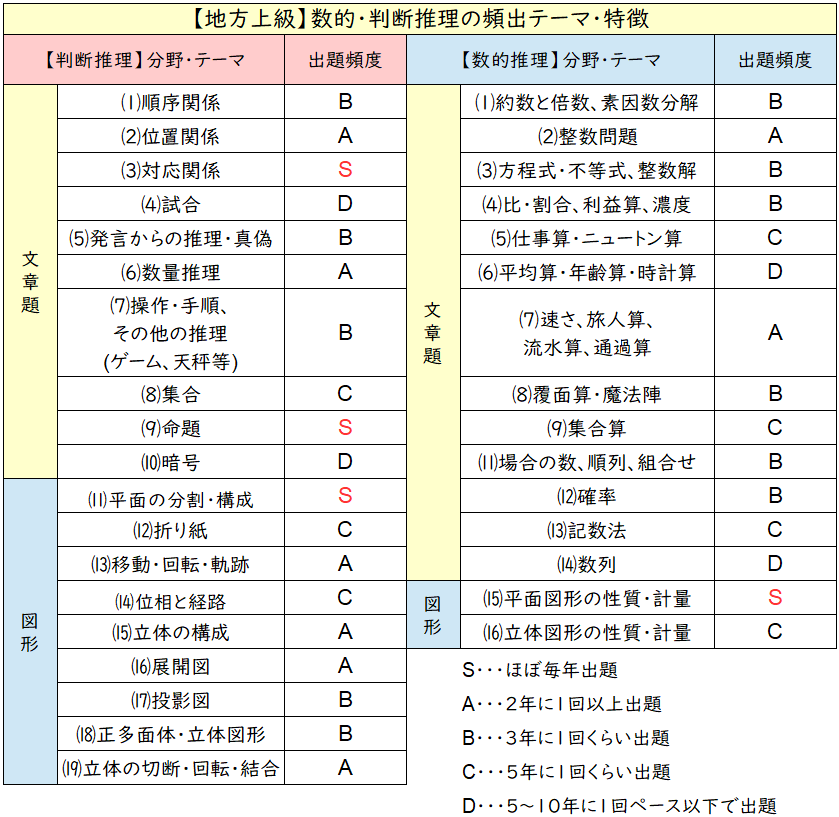※地上は過去問が見れないので市販のものを参考にしています。
パッと見てわかる通り、ココから出題されやすいってテーマが無いんですよね！
いろんな分野からまんべんなく出題されているイメージです。
中でもメジャーなテーマ
「(1)~(7)の文章・数量からの推理系」、「(9)命題」、数的は「(2)整数問題」「(4)比・割合」「(7)速さ」などはよく出てますよね！
しいて言うなら「確率」系の出題が他の試験より少ない、「立体の体積や表面積」を求める問題が他の試験より少し多いというのが特徴だと思います。
メジャーな分野からの出題が多いといえど、バランスよく出題されるのが地方上級の特徴なので、テーマごとに基礎的な問題をきちんと勉強しておきたいですね！
→みんなが取れる正答率50％以上の問題を落とさないことを目標に！
【市役所】数的・判断推理の出題テーマ＆特徴
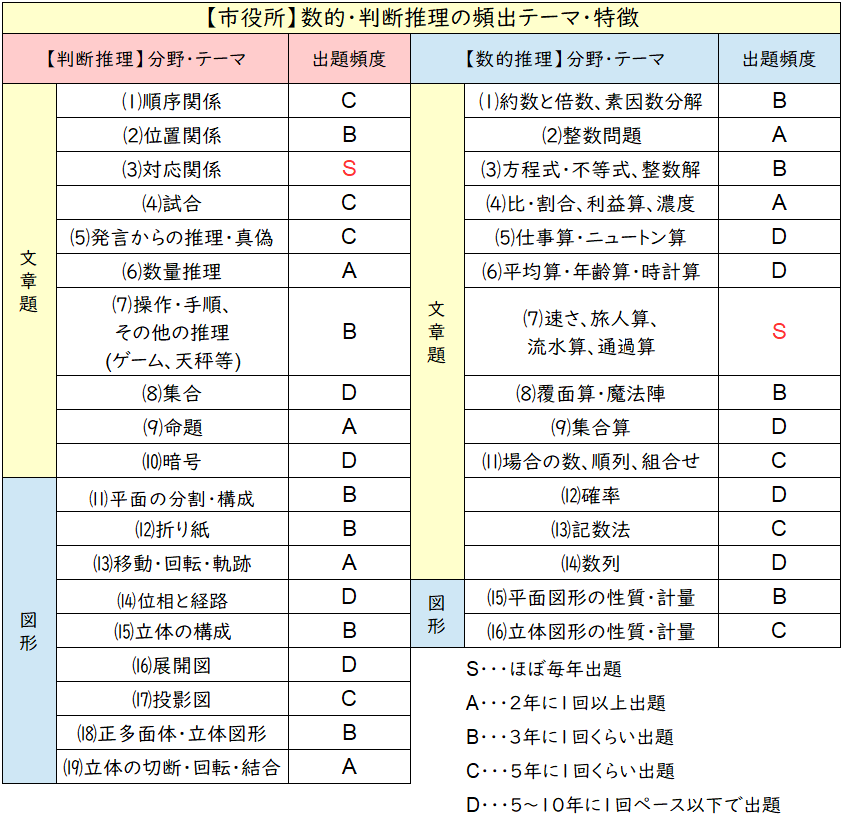※市役所は過去問が見れないので市販のものを参考にしています。
パッと見てわかる通り、地方上級と同じでココから出題されやすいってテーマが無いんですよね！
いろんな分野からまんべんなく出題されているイメージです。
中でもメジャーなテーマ
「(1)~(7)の文章・数量からの推理系」、数的は「(2)整数問題」「(4)比・割合」「(7)速さ」などはよく出てますよね！
逆に「確率」の問題がほとんど出てないのが特徴かなと思います。
地方上級と同様、メジャーな分野からの出題が多いといえど、バランスよく出題されているので、テーマごとに基礎的な問題をきちんと勉強しておきたいですね！
→みんなが取れる正答率50％以上の問題を落とさないことを目標に！
【都庁】数的・判断推理の出題テーマ＆特徴
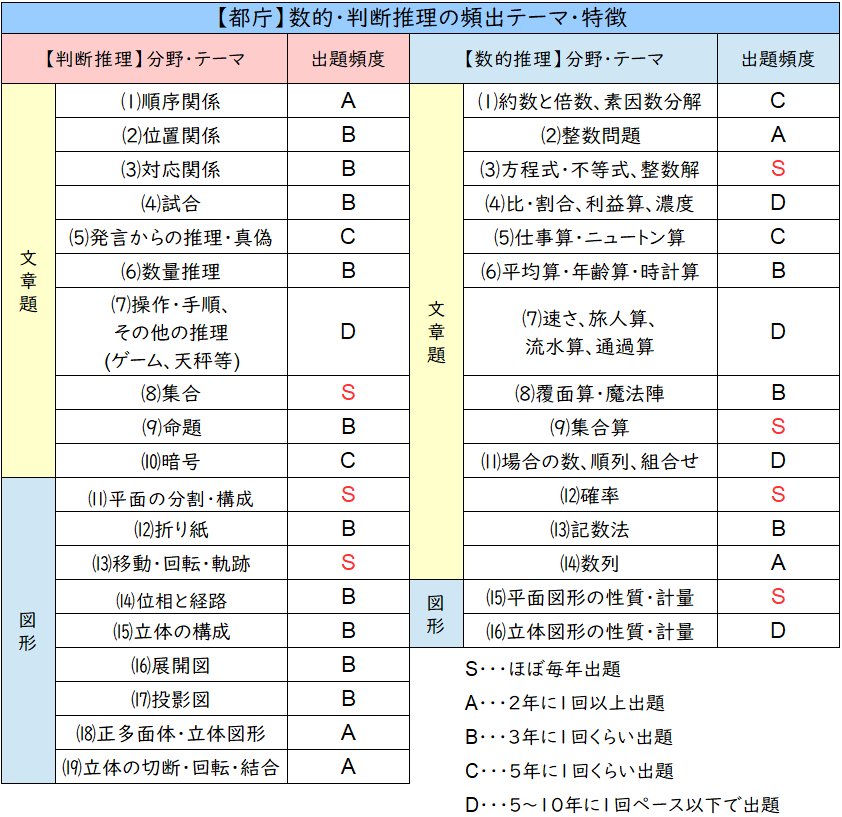
都庁の試験は超特徴的です。
出題されやすい分野とか出題のされ方などが他の試験と少し違うので
都庁を志望している方は解法を覚えたらどんどん過去問演習を行っていくことが大事なんじゃないかなと思います。
「集合」が毎年出題されてたり、「方程式・不等式、整数解」、「記数法」や「数列」の問題が多かったり、逆に「数量推理」「速さ」「比・割合」の問題が少なかったりとかなり特徴がありますからね！
そして(1)~(7)の推理系の出題が他の試験に比べて少ないのも特徴的だと思います。
過去の問題の値や文章を変えて使いまわしているような問題が出たりもしますので、逆にいえば、参考書を使わなくても過去問を10年分やっておくだけで本番でもいい点とれると思います。
【特別区】数的・判断推理の出題テーマ＆特徴
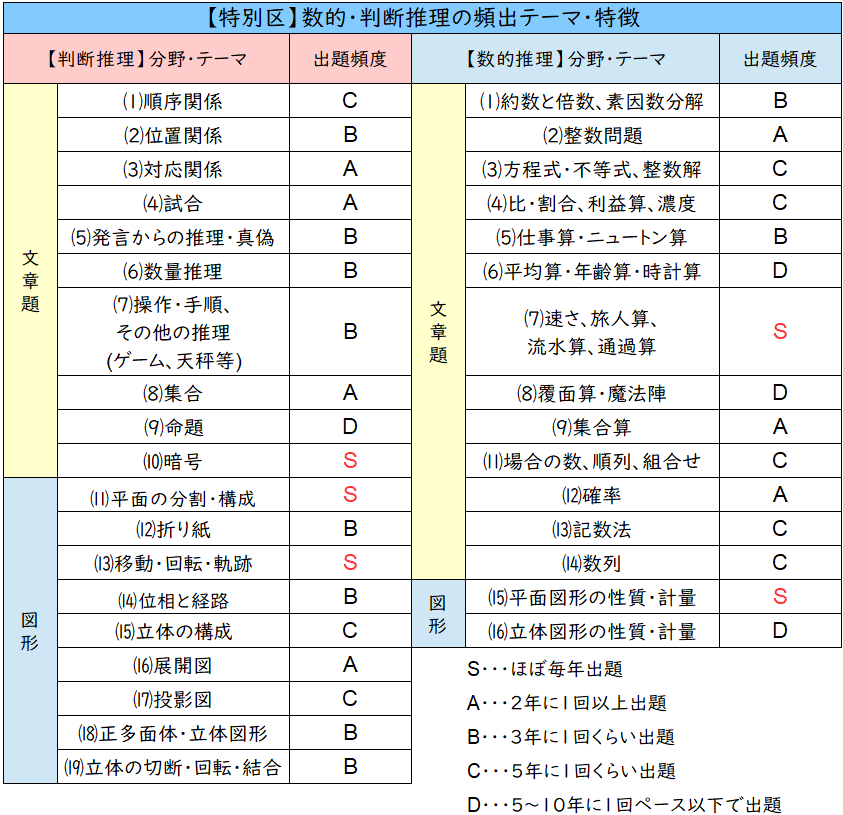
特別区の数的もかなり特徴的です。
毎年似たような問題が出題されているので対策しやすい試験かなと思います！
まず他の試験に比べて問題の難易度が低いものが多いです。
そして、特に特徴的なのは「暗号」ですね。
他の試験では出題頻度がかなり低いですが、特別区ではほぼ毎年出題されています。
次に特徴的なのが「試合」が多いことですね！
試合も重要テーマではあるのですが、特別区は他の試験に比べて「試合」の出題が多いです。
また「速さ」や「図形の面積」を求める問題も毎年出題されていますので、苦手な方も基礎的な問題は落とさないようにしたいですね！
後は最近「展開図」や「軌跡」を利用した問題が増えていると思います。
ココらへんもおさえておきたいですね！
当然、対応関係や位置関係の問題もよく出ますし、ある程度まんべんなく出題されているので、実際に受験する方は「過去問演習」を大事にしていただければと思います。
この記事を書いた人
【よくある質問】
この手の質問って結構多いんですよね！
→私に話しかけてくれることは非常にありがたいですし、その行動力は評価できますが、このような質問をしてしまう方は黄色信号だと思います。