【力学：エネルギーと運動量】簡単な頻出テーマも捨てる気？意外に問題難易度＆理解難易度が低いのがこの分野！

東京都庁・特別区で頻出！

エネルギーって…実は超簡単なんですね！
特に公務員試験に出ている問題なんて難易度超低いです！
しかも、東京都庁や特別区ではよく出題されているんですね～！
→個人的にはオススメのテーマかなと思います。

主には公務員試験の物理対策として、
中学～高校の物理の分野すべてを解説していきますが、
もちろん中学生高校生の方が見ても参考になると思います！

ではさっそく【エネルギーと運動量】分野の勉強をしていきましょう！

私は物理って言う科目がすごく好きなんですね。
今は公務員試験のせんせいとして、受験生の皆さんに物理が基礎となってる構造力学や水理学、土質力学なんかを教えています。
このページは『物理初心者の文系の方』に向けて書いたものです！

もちろん教養試験対策だけじゃなくて技術職の人の工学の基礎対策にもなると思います！
じゃあみんなが苦手な力学分野の対策スタート(^o^)/[/voice]

【力学：エネルギーと運動量分野】初心者向けに４項目を解説！

エネルギーとか運動量とかってイメージしにくいので勝手に苦手だと思いこんでしまっている人が多いと思います。
はじめにいっておきます！
この分野から出題されている問題は超難易度低いです！

この４つのテーマについて、基礎的な部分がわかるよう図でわかりやすく解説していきますね！

確かに教科書を読んだだけでは理解するのが難しいかもしれませんが
誰かに教えてもらえば超簡単だと思います！

個人的にはコスパ◎かなと思っています！
では、本編にまいりましょう！

確かに元をたどっていくと難しいかもしれませんが
公務員試験の物理対策として取り組むなら
理解するべきポイントは決まっていますし、なんせ簡単です！
是非ともココは落とさないようにしていただきたいなと思います！

【仕事と運動エネルギー】サラッと読んでおけばOK！

いきなり物理的な考え方について話すと理解しにくいと思いますので
まずは「エネルギーって何か」というところから紹介！

簡単にいうとエネルギーって
「ものを動かす原動力」のことですよね？
例えば、ガソリンでも電機でも走る車があったとして、どちらも同じ重さだったとします。
車ってすごく重たいですよね！
そんな重い車をある量のガソリンだと200km、ある量の電気では800km動かすことができたとします。
みかたを変えると、右側の図は「４倍のエネルギーを持っている」と評価することもできますよね。

人間でも同じですよね。
50kgの荷物をA君は5m、B君は10m動かせたとすると
B君はA君の２倍エネルギー(原動力)を持っていることになります。

なんとなくエネルギーについてイメージできたところで物理の世界に入っていきましょう！

【仕事の定義】力×距離＝仕事

物体に一定の力F[N] を加え続けて、その力の向きに距離x[m]だけ動かすとき、その積Fxを、力が物体にした仕事といいます。

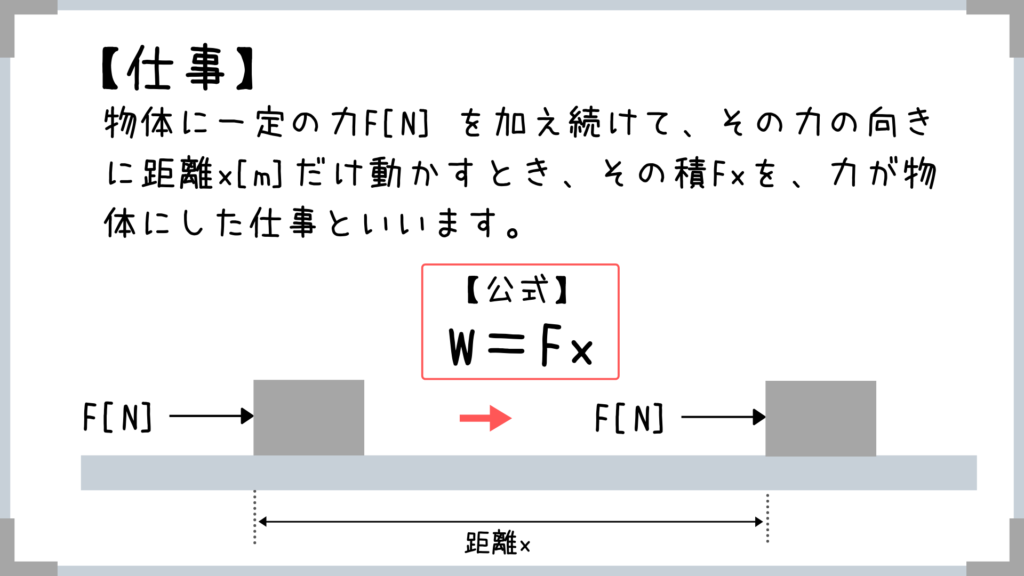
難しいことは考えずに「力×距離＝仕事」と覚えておけばOK！

ということで仕事の単位は[N・m]
→これを１J(ジュール)と言い、エネルギーの単位と等しくなります！
(力×距離[N・m]→仕事[J]って知識として覚えておくとこの分野は理解しやすくなると思います）

力の向きと移動の向きが違うときは、力を分解して移動に寄与する力の成分だけを考えなければいけないんだ！
ということで力が斜めに働くときの仕事は
「W=Fcosθx」ですね！

【運動エネルギー(重要)】コレは試験でめちゃくちゃ使います！

運動エネルギーを使用する問題は公務員試験でも頻出です！
簡単に理解できるので絶対に覚えておきましょう！

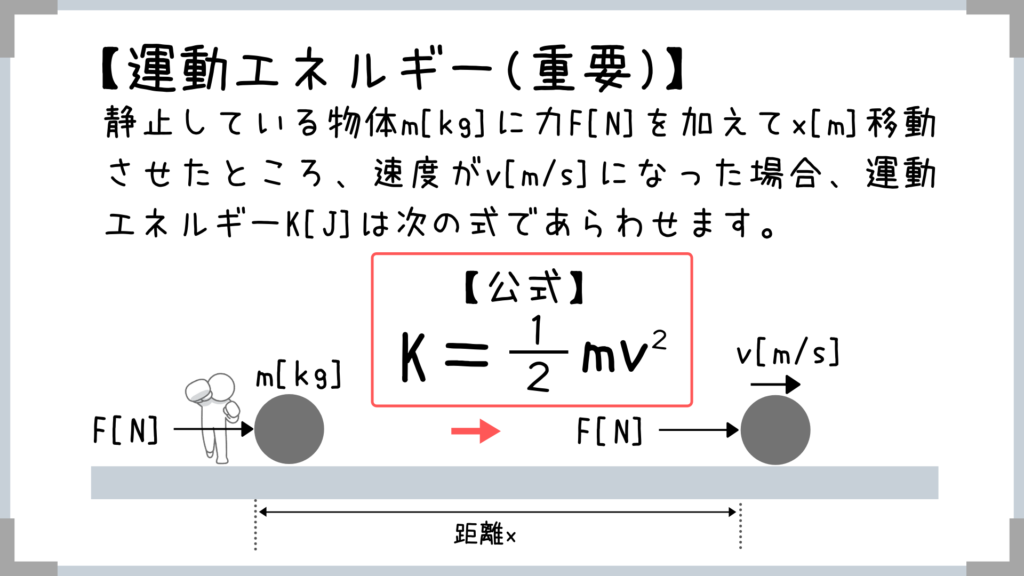
理屈なんてどうでもいいので
「運動エネルギー＝mv²/2」というのは覚えておきましょう！

質量があって、それが速度を持っているなら
その物体はエネルギーを持っているということになります！

実は②物体の運動でお話した内容を完璧に理解できていると導くこともできちゃうので、興味がある方は自分で導いてみてください。

【エネルギーの原理】出題率低

イメージだけ簡単に紹介しちゃいますね！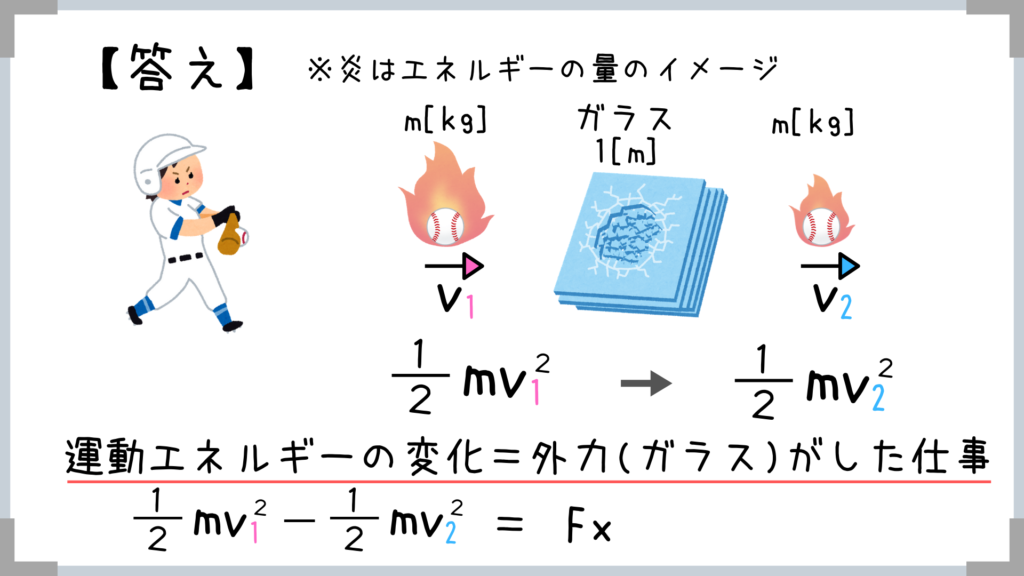

※厳密にいうと少し違うのですが、こんな感じで覚えておけば問題は解けちゃうと思います！

運動エネルギーの変化は外力がした仕事に等しいということですね！

【力学的エネルギーの保存】出題されるポイントは決まってる！

公務員試験では出題されるポイントがある程度決まっているので
重要なポイントだけ紹介したいと思います。

まずは「位置エネルギー」から紹介！

【位置エネルギー】非常によく使う公式！

先ほど物体は「速度」を持っているだけで「エネルギー」を持っていると言いましたが
実は「高さ」を持っているだけでも「エネルギー」があると言えるんですね！
高い所にある物体は重力によって落下しますが、この力によって仕事をすることができますからね！
コレを重力による位置エネルギーと言います！

そして、位置エネルギーの大きさUは
「U=mgh」とあらわせます。
コレは公務員試験でも非常によく使用する公式となります！

細かい話は次の「力学的エネルギー保存の法則」で紹介していきますね！

【力学的エネルギー保存の法則】位置E＋運動Eは一定ということ！

簡単に言うと力学的エネルギーとは、物体がもつ「位置エネルギー」と「運動エネルギー」の和のことです！

そして、物体に保存力(重力や弾性力や静電気力)のみがはたらく場合、その物体の力学的エネルギーは一定になります。
→これを力学的エネルギー保存の法則といいます。

「力学的エネルギー＝位置エネルギー＋運動エネルギー＝一定」

とりあえずこんな感じで覚えておけばOK！

とはいってもイメージしづらいと思いますので、
実際に例を挙げて紹介していきたいと思います！

位置エネルギーと運動エネルギーを足したものが力学的エネルギーだと言いましたが、
コレは実はどこの地点でも「一定」なんですね！（炎の大きさの合計はどこ一定です！）

→このようにどの地点で見ても力学的エネルギーが一定に保たれることを「力学的エネルギー保存の法則」というわけですね！
→「イコール」で結ぶことが出来る！

だからh地点と0[m]地点に着目してみると
h地点では力学的エネルギー＝mgh＝炎(一定)
0[m]地点では力学的エネルギー＝mv₂²/2＝炎(一定)
→「mgh＝mv₂²/2」という式が成り立つわけですね！
(位置エネルギーがすべて運動エネルギーに変わったと言い換えることもできます）

（自由落下の公式を考えてみると0[m]地点までの距離h=gt²/2で、v=gtですよね？
→この２式よりh=v²/2gとあらわせるのでmgh＝mghとなり、式の証明もできる）

まぁ難しいことは考えずに
位置エネルギー＋運動エネルギー＝一定

これだけは覚えて下さい！

とはいっても実際に使ってみないとイメージわきませんよね！
例題と演習問題を１問ずつやってみましょう！

【力学的エネルギー保存の法則の例題】鉛直投げ上げでも使用可！

あえてこの問題をチョイスしてみました！
さぁ皆さんは解けそうですか～？

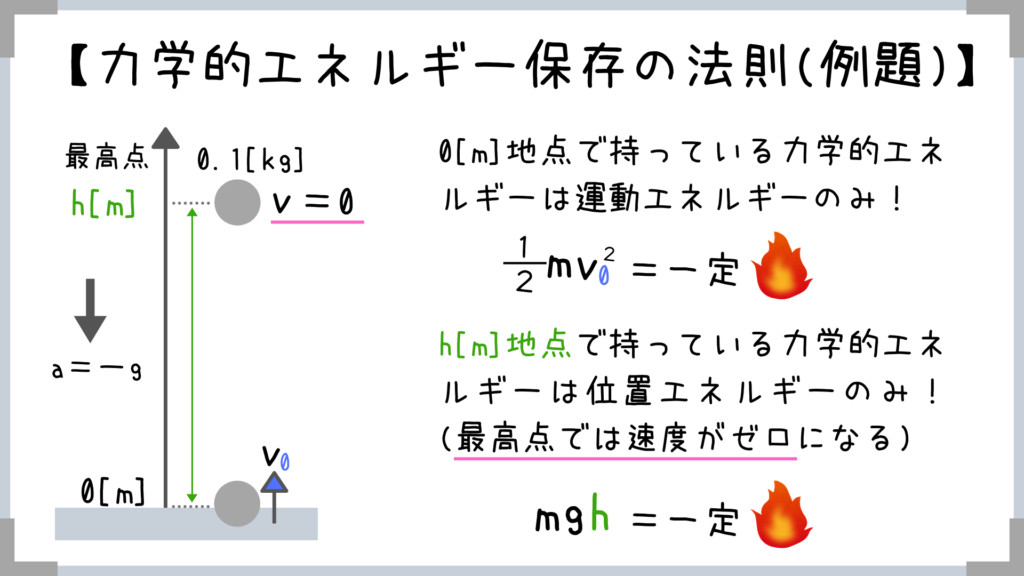
最高地点では速度がゼロになりますから、運動エネルギーはゼロとなり、位置エネルギーのみとなります！
逆に0[m]地点では位置エネルギーがゼロで、運動エネルギーのみですよね！
力学的エネルギーはどの地点でも一定となるので、これらのエネルギーの大きさは同じということになります！

運動エネルギーの炎は位置が高くなるにつれて少なくなっていき
速度がゼロになった地点で運動エネルギーもゼロとなり
最初に持っていた運動エネルギーすべてが位置エネルギーに変換されてしまったと考えられますよね！

そして、この問題にはもう１つ皆さんご存じの解法がありますよね！

『鉛直投げ上げの公式』を利用して解いてもOKです！

このように、鉛直投げ上げや自由落下、放物運動の問題でも力学的エネルギー保存の法則は使うことができるんですね！

使うのには慣れがいるけど、今基礎を覚えて実際に過去問を解いてみるとすぐに解けちゃうと思います！
よく出題されているパターンの問題をもう１問解いてみましょう！

【力学的エネルギー保存の法則の演習問題】楽勝♪

こんな形の問題や滑らかな斜面をくだっていく物体の速度を求める問題がでたら基本的には「力学的エネルギー保存の法則」をつかいます！

ココまでの話をきちんと理解してくださった皆さんならアとイはすぐにわかっちゃいますよね！
(はじめてこの問題を見たとしてもわかりそうですが…(笑))

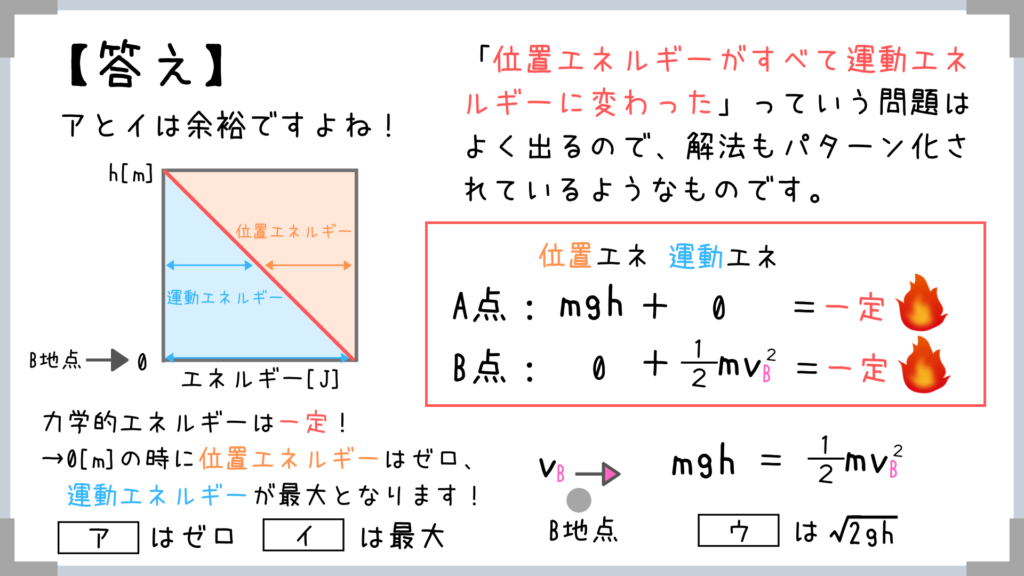
難しそうに見えて簡単でしょ？
コレ、実際に東京都庁で出た問題ですよ～！

この問題のように、「位置エネルギーがすべて運動エネルギーに変わった」ってパターンの問題はよく出るので要チェックです！

高さがhの時、v_Bが√2ghになるって公式として覚えて良いレベルだと思います。

ちなみに、今回は滑らかな面が円形でしたが、滑らかな部分が斜めの下り坂だったとしてもB点での速さは√2ghになります！

このグラフを見るとわかりやすいですよね！
hが高くなっていったとしても横ラインの合計値は一緒になります。
じゃあ力学的エネルギーにも慣れてきたってことで
次は「運動量」について勉強していきましょう！

【運動量の基礎】都庁と特別区志望者は要チェック！

運動量保存の法則は東京都庁と特別区では頻出テーマなので、受験する方はきちんとおさえておきたいところ！
しかも、出題されている問題は超単純！
これはもう勉強するしかありませんね～！

お友達には内緒で今のうちに勉強しちゃいましょ！
まずは『運動量の基礎知識』から紹介していきますので
サラッと見ておいてください！

【運動量とは？】→「勢い」だ！

いきなりですが皆さん、「ボーリング」がうまい人の特徴を知っていますか？
まっすぐ投げられる、重い球を投げられる、速い球を投げられる…
そうですね！
投げた球がまっすぐ飛ぶのは大前提として
球に『勢い』がある人ですよね！

大げさな話、５ポンドのボーリング球をふら～ってゆっくり投げたところでピンは全然倒せませんよね？
それは球に『勢い』がないからです！

物体の運動というのは、物体の質量が大きいほど、物体の速度が大きいほど、激しく動くと思います。
物体の運動の激しさ(勢い)を表すとき、質量と速度をかけたものを用いる！
→この勢いの大きさをあらわしたものを『運動量』といいます。

難しいことは考えずに、『質量×速度＝運動量』と覚えておけばOK！
実際こんな理屈を覚えてなくても
問題が解ければOKです。

【運動量原理】サラッと見ておけばOK！

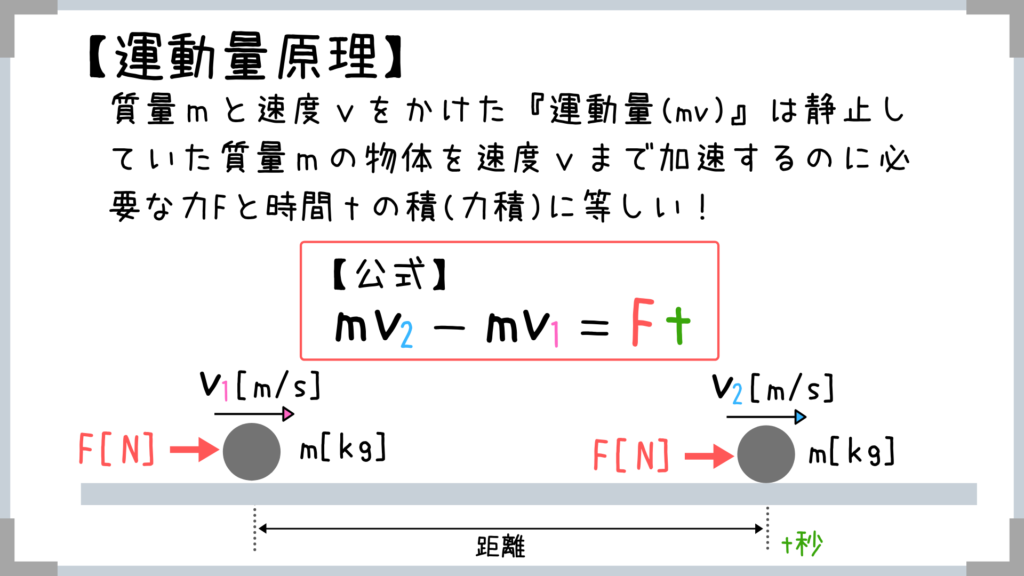
質量ｍと速度ｖをかけたmv『運動量』は静止していた質量ｍの物体を速度ｖまで加速するのに必要な力Fと時間ｔの積(力積)に等しい！
（加速度aはv₂-v₁/t、これを運動方程式に代入するとこの式が導けます）

まぁこいつも難しいことは考えずに、結果だけ知識として知っておけばOKです！

【運動エネルギーと運動量の違い】まったくの別物！

一応、理解が出来ていない方が多いので、運動エネルギーと運動量の違いをサクッと紹介！
単位に着目してみると考えやすいと思います。

まぁ問題が解ければいいので覚える必要はありませんが、簡単に言うとこういう違いがあります！
あとは向きが関係あるのが運動量ですね！

知らなくても問題が解ければいいので次に行きましょう！

【運動量保存の法則】都庁と特別区は頻出テーマ！

直近では2017年の特別区で超簡単な問題が出題されています。
過去には数年連続で出題されていたこともあります。

問題を見た瞬間に「あ、運動量保存の法則を使う問題だな」ってすぐにわかるところがまずイイですよね。
そして、「解き方が決まっている」という点がオススメポイントです！

物理が苦手な方でも解き方を覚えちゃえば、容易に答えまでたどり着けちゃうと思います。
ということで皆さん頑張って勉強していきましょう！

【運動量保存の法則とは？】簡単すぎ！

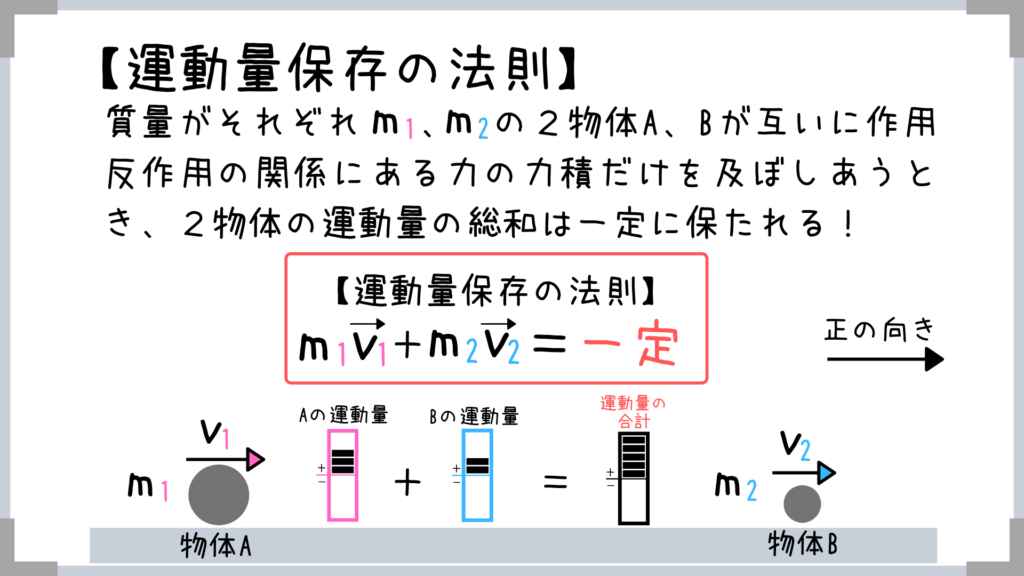
運動量保存の法則を簡単に言うと、
「どんなに複雑に運動しても合計の運動量は変わらない」ということです！

まぁこの式だけだとイメージしにくいと思いますので
さっそく物体をぶつけていきましょう！

【２物体の衝突】よく出題されています！

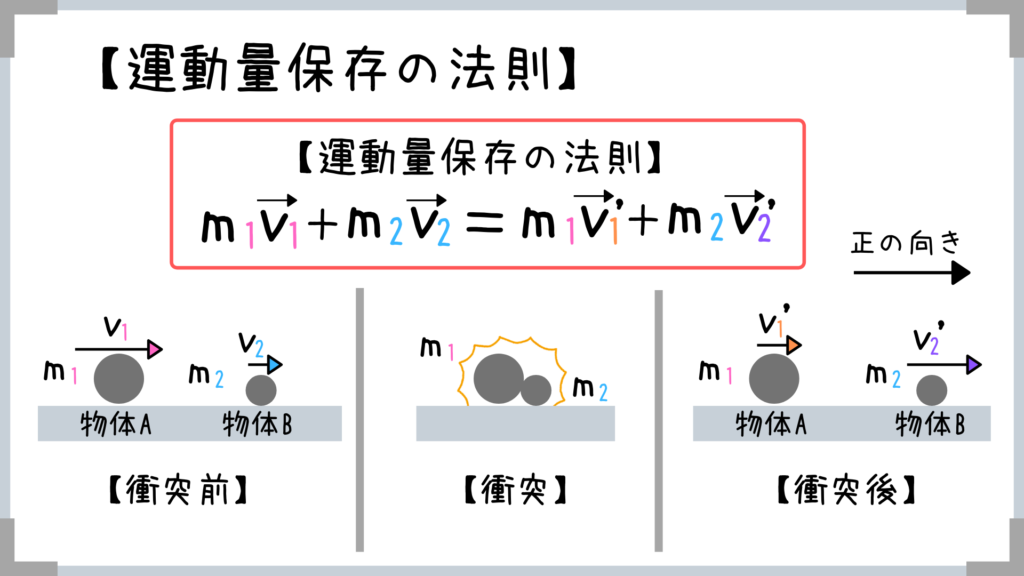
こうやって図示して考えてみると、
運動量保存の法則も理解しやすいですよね！
要は「衝突前の運動量の合計＝衝突後の運動量の合計」ということです。

では実際に問題を解いていきたいと思いますが
その前にもう１つ知っておかなければいけない公式があります。

それは「はね返り係数」と呼ばれるもの。
コレも公式を言語情報としてインプットすると理解しやすいので、
さっそく式を見ていきましょう！

【はね返り係数】３つのパターンがあります！

「うわ、はね返り係数って難しそう…」
って思うかもしれませんが、実はめちゃくちゃ単純な話なんですね！

「ぶつかる前と後の速さの比」をあらわしただけで
「ぶつかる前は〇[m/s]で走ってたけど、ぶつかったら–e倍になって速度が△になったよ」ってことです！

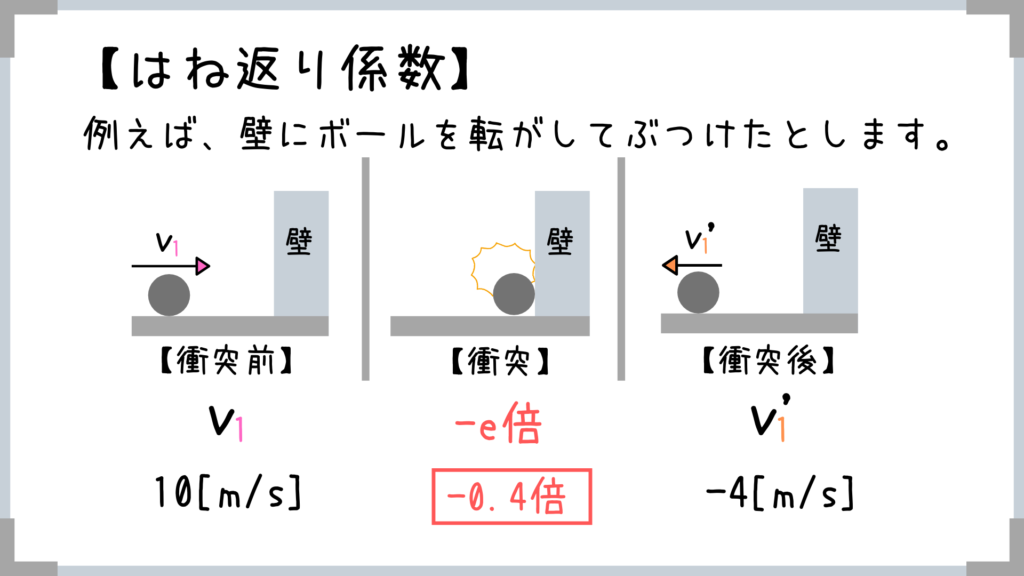※マイナスがつくのは相対速度の向きが逆になるため。
簡単でしょ～！
(コレは壁の速度を衝突前と後それぞれ0として公式に入れて考えればOK）
なんでこんなめんどくさそうに見える公式を使うのかというと
コレは「相対速度」っていう意味なんですね！

車に乗りながら電車とすれ違う～とか
自転車に乗って車に追い越される～とかいうアレのことです！
自分が60kmの自動車に乗ってて
60kmの電車とすれ違ったら
自分が静止している状態で見る120kmの電車の速度に見えるわけですね！

同じ方向に進んでたら引き算、反対方向に進んでたら足し算をすれば相対速度が求められます！
この公式は同じ方向と仮定しているからv₁-v₂、v’₁-v’₂としているわけなんです！

公式の意味もわかったところで
はね返り係数の３つのパターンを紹介していきたいと思います！

弾性衝突というのは、物体Aの速度が物体Bの速度にすべて変換されるということです。
物理の問題としては出題されることはありますが
現実世界では存在しないんじゃないでしょうか。
「ニュートンのゆりかご」という装置は有名ですけどね！

日常生活で見られる衝突というのはだいたい「非弾性衝突」です！

今回は以下の３つの問題を解いていきます！

• 完全非弾性衝突
• 非弾性衝突
• 衝突×力学的エネルギー保存の複合問題

【完全非弾性衝突の演習問題】2017年の特別区の問題！

「一体となって進んだ」と書いてあるので、
はね返りもくそもありません！
完全非弾性衝突となります！

答えを導く手順は決まっているので、メモしてください！

あとは計算するだけですね！
基礎的な問題はすべてこの４つの手順で解くことができます！

さっそくやっていきましょう！

衝突前と衝突中、衝突後の図を描くのは超大事！

そして、必要な値をすべて図示していきます！

運動量保存の法則により、衝突前の運動量の和と衝突後の運動量の和は等しくなる！
等式で結んでvを求めれば終わりです！

少しは【運動量保存の法則】の使い方のイメージがつかめましたか？

次は非弾性衝突の問題を解いていきます！
この問題が理解出来たら及第点！
ではまいりましょう！

【非弾性衝突の演習問題】重要です！コレが解けたら１点取れるかも！

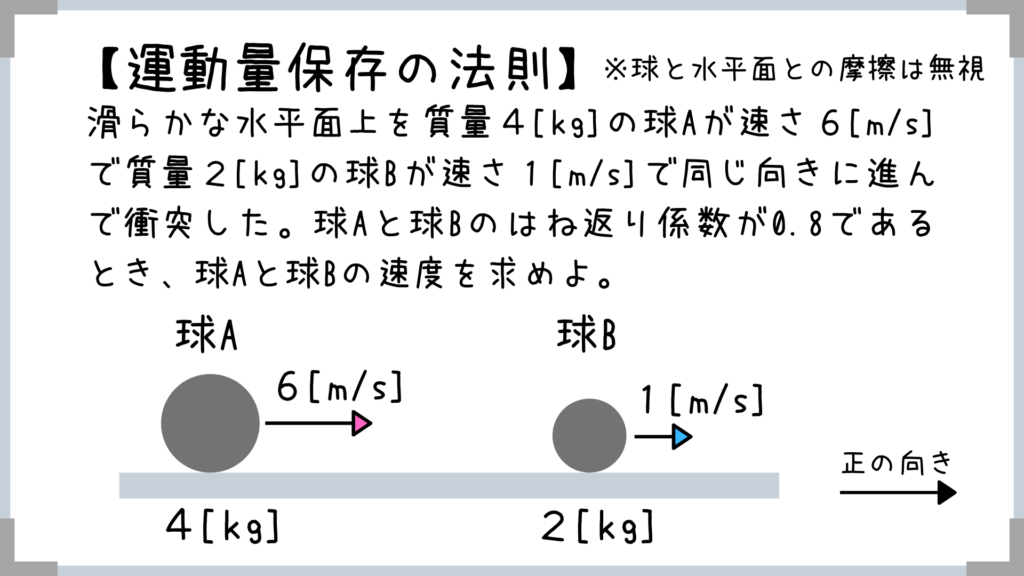
先ほども言いましたが
この手の基礎問題は解く手順が決まっています！

先ほど解いた【完全非弾性衝突の演習問題】と流れは同じです！

ではやっていきましょう！

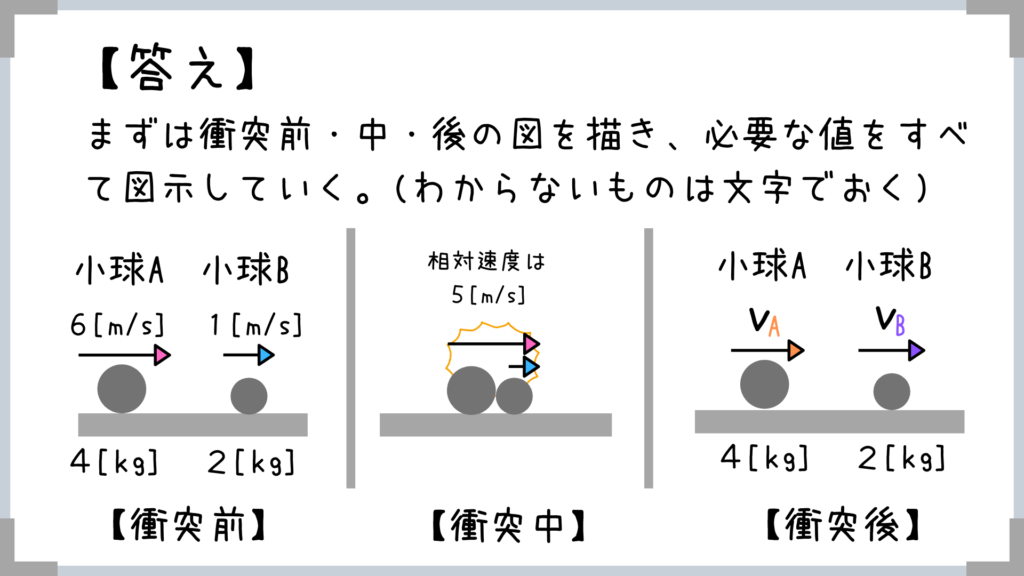
ちなみに、衝突中の図を描くのは「ぶつかる直前の(相対)速度を間違えないようにするため」です。
（この手の問題では無理に描く必要はありませんが、床に物体を自由落下させる問題などではミスを招きがちなので、描いておく癖をつけておくといいと思います）

運動量保存の法則の式を立てて計算すると①の式が導けますね！
左辺を見るとわかるのですが、運動量の合計は26になるので、右辺の式の合計も26にならなければ保存しているといえません。

あとは「はね返り係数の式」に値を代入して、この式と「運動量保存の法則の式」から答えを求めるだけ！
はじめてとくと少し難しく感じるかもしれませんが、
やっていることは単純ですし、
解法パターンが決まっているので
受験生にはオススメしています。

慣れたらこの手の問題が出たら「ラッキー♪」って思うようになりますよきっと(笑)

力学的エネルギーと運動量をあわせた問題とかも出題されているので、参考書中にある複合問題も触れておくといいと思います。
複合問題も「力学的エネルギーの基礎」×「運動量保存の法則の基礎」という問題ばかりなので、理解難易度は低めです。

【衝突×力学的エネルギー保存】複合問題もやることは一緒！

仮に力学的エネルギーとの複合問題が出たとしても、
衝突の問題として解かせる前に
力学的エネルギー保存の法則から衝突直前の速度を求めさせるだけというものが多いです。

例として、先ほどの衝突の問題に力学的エネルギーの要素を追加した問題を１つ紹介。

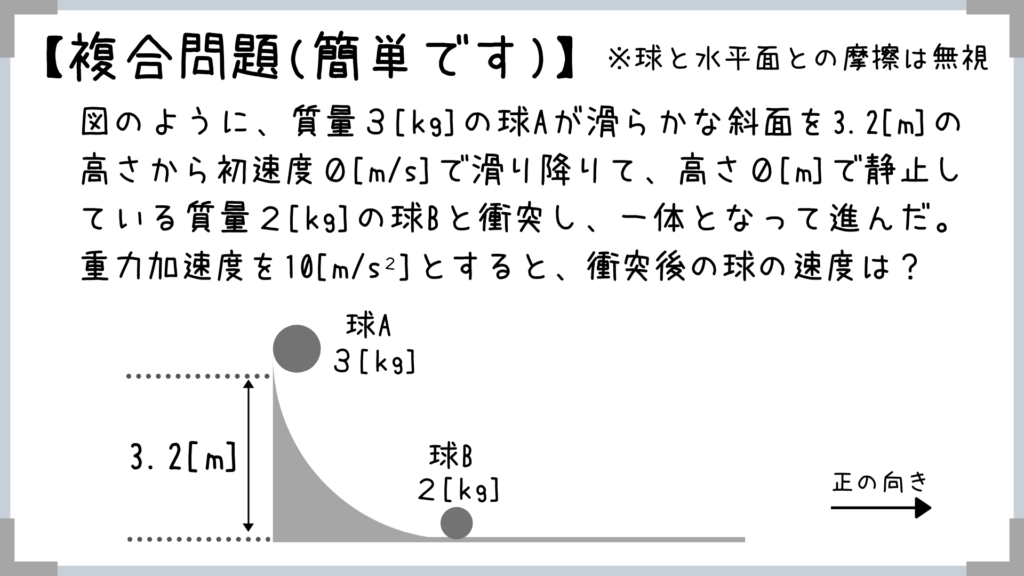
物体が滑らかな斜面をくだる問題が出てきたら、
基本的に「力学的エネルギー保存の法則」を使います！
→球Aが球Bにぶつかる直前の球Aの速度がわからないと、運動量の式は使えませんよね！

コイツを力学的エネルギー保存の法則で求めていきます。

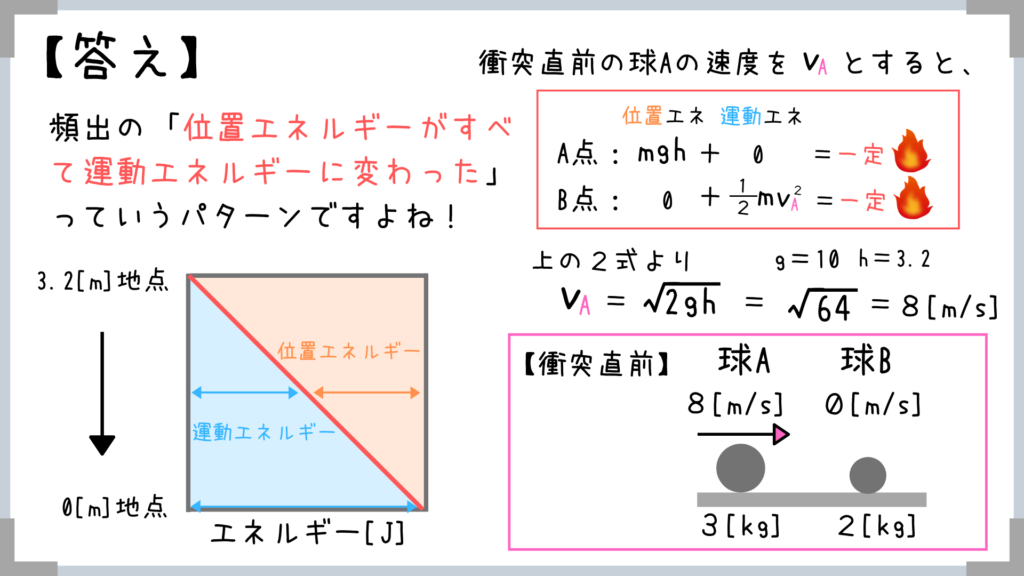
力学的エネルギーの使い方は慣れてきましたか～？

3.2[m]地点では位置エネルギーが最大、運動エネルギーがゼロ
0[m]地点では位置エネルギーがゼロ、運動エネルギーが最大となりますよね！
→お馴染みのパターンなのでv=√2ghを公式として覚えていいレベル。

速度が求まったら、
衝突(運動量保存の法則)の問題として４つの工程を意識して解いていけばOK！

よし解いていくぞ～って思って気付くことがありますよね！
さっき解いた2017年の特別区の問題と要領が同じ…！

そうなんです。
こうやって基礎的な部分を複合させているだけで
少し難しく見えちゃいますが
やっていることは単純なんですね！
ということでこの先の解法は先ほどの問題とまったく同じ！

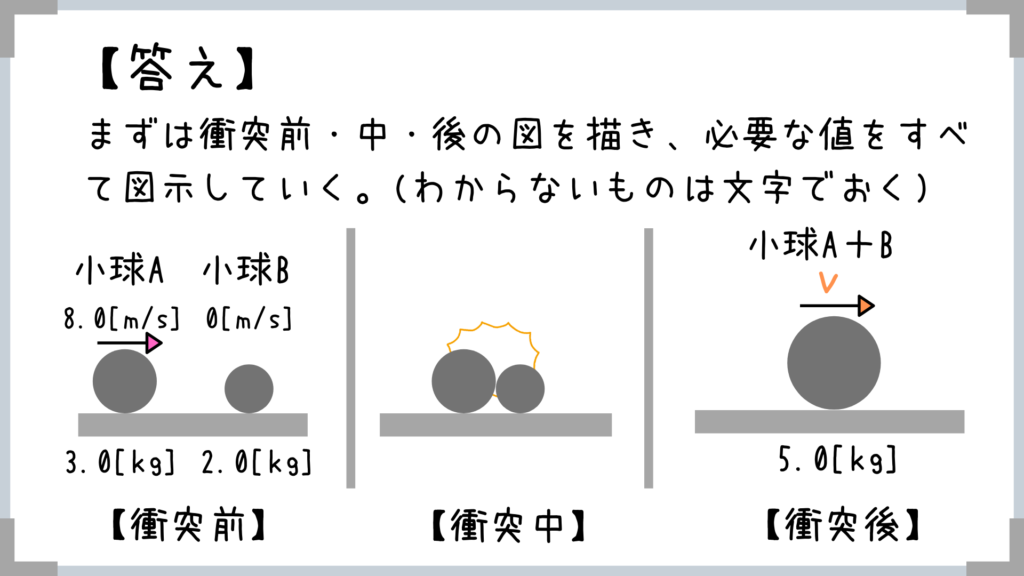
これでこのページは終わりです！
エネルギーと運動量について解説しましたが、
どうでしょうか？

最初は難しく感じるかもしれませんが、
すぐに慣れると思いますので
「出たらラッキー♪」
ってなりますよ！

ちなみに、球を壁にぶつけたり、球を床に落下させたりする問題も
「衝突」と「はね返り係数」の知識を使えば簡単ですよね！
解法はすべて同じですから、これらの問題はご自身で挑戦してみて下さい！

では長々とお疲れ様でした！