初心者の方に向けて、『身近な例』で物理の問題の解説をしていきたいと思います!
実は難しそうに見える問題でも、身近なもので考えてみると
「あ~なるほどな」
って思うことが多いんですよね~!
主には公務員試験の物理対策として、
中学~高校の物理の分野すべてを解説していきますが、
もちろん中学生高校生の方が見ても参考になると思います!
ではさっそく【力のつり合い】分野の勉強をしていきましょう!
- 今ココ→①力のつり合い
- ②物体の運動
- ③エネルギーと運動量
- ④周期的な運動と慣性力
- ⑤電気と磁気(オススメ)
- ⑥波動
- ⑦熱と原子、その他

目次
【力のつり合い分野】初心者向けに7項目を解説!
中学~高校物理の中でも、まずはじめに【力のつり合い】分野から紹介していきたいと思います!
この7つのテーマについて、基礎的な部分がわかるよう図でわかりやすく解説していきますね!
物理って基礎が大事ですから、最初でつまずいちゃうとちょっとひねった問題や応用的な問題に対応できなくなっちゃうんですよね…
ということでこのページは説明が丁寧すぎるかもしれません!
その点ご了承いただけると幸いです。
まぁごちゃごちゃ言っても仕方ないので、本編にまいりましょう!
【重力(2力のつりあい)】ココでつまずくとアウト!
重力って言うのは重力の大きさ(W)のことで、
W[N]=mg=質量[kg]×重力加速度[m/s2]であらわされます。
(Nというのはニュートンのことで、力の単位のことですね!)
まぁいきなりそんなこと言われてもわけわからないと思いますので、
まずは力のつり合いの基礎的な問題から解いていきましょう!
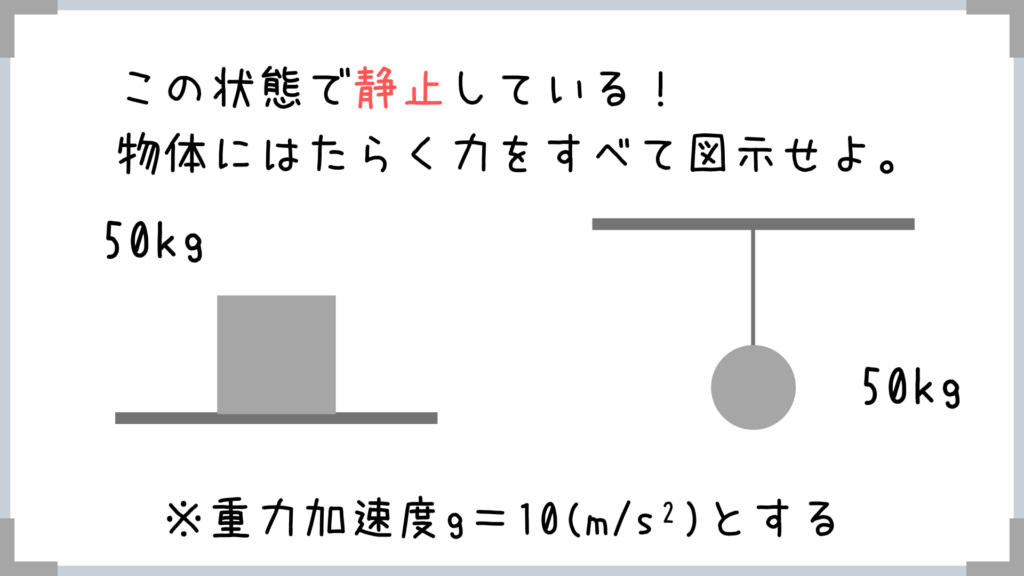
…いきなり力を図示しろって言われてもねぇ。
まずはポイントから紹介!
自分が物体になって考えてみる!
→自分にはたらくちらかをすべて図示してみる!

自分が物体になってどこに力がはたらくか考えてみましょう!
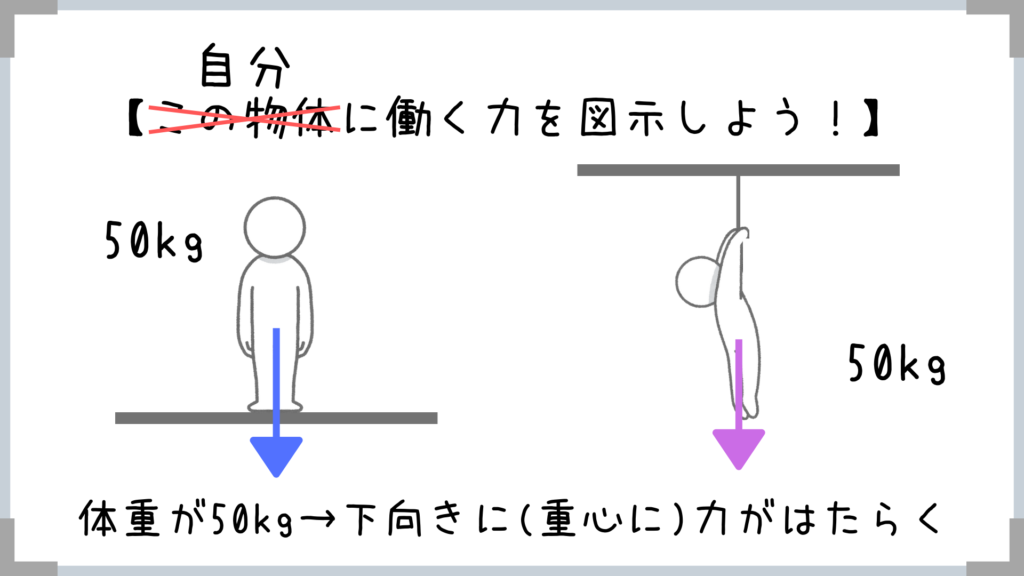
とりあえず、自分の体重分、下向きに力がはたらいていますよね!
そして物理の考え方で大事なポイント!
- 「静止している」ということは、物体にはたらくタテ・ヨコ・回転させる力がつりあっている!
- 基本的に、物体と物体が接触している部分には力がはたらく!
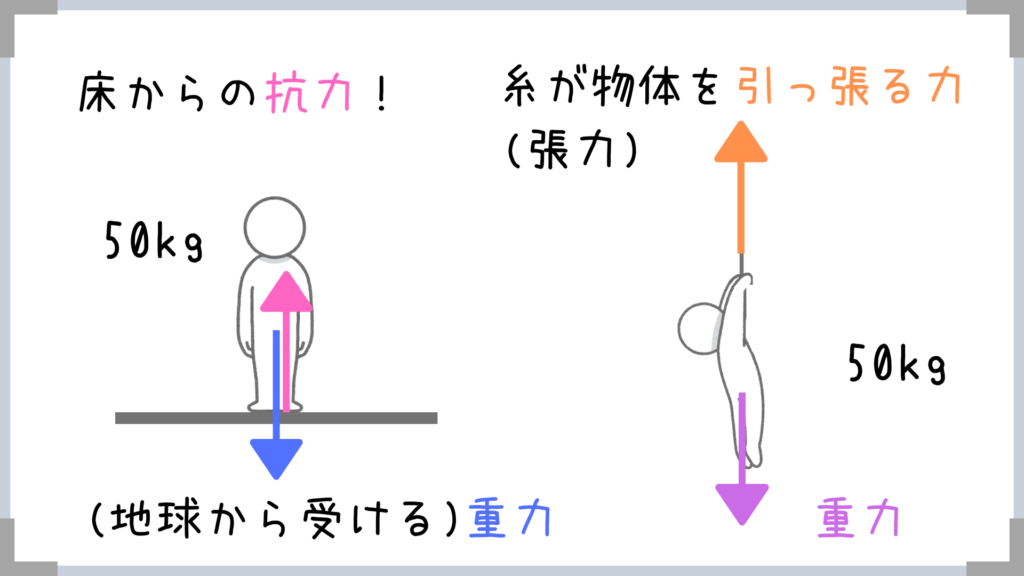
ポイントをおさえて力を図示すると↑こんな感じ!
実際に自分がぶら下がったら、手に負担がかかりますよね?
→このような部分には基本的に力がはたらいています

では先ほどの問題に戻っていきましょう!
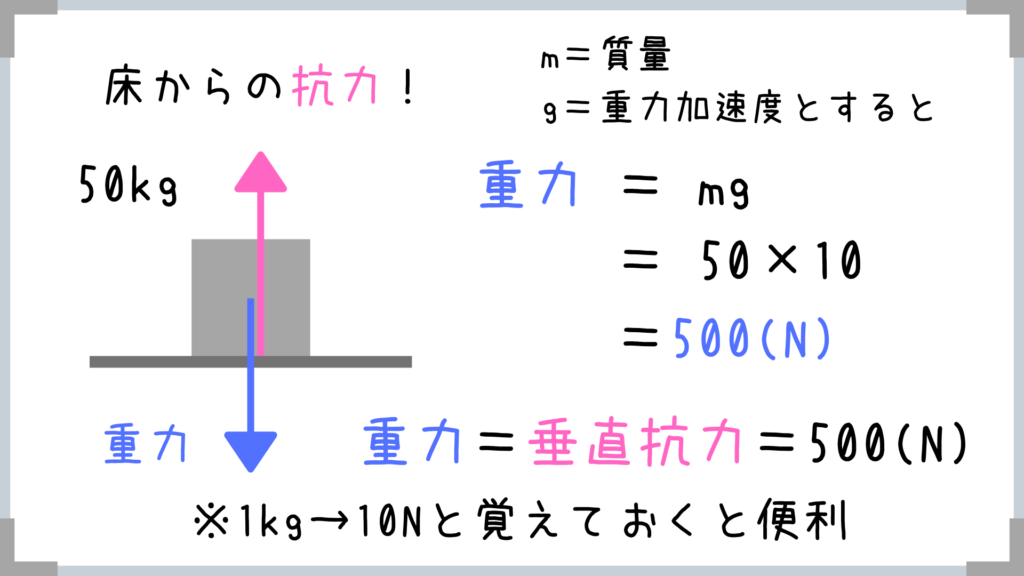
静止しているということは、力が釣り合っています!
→この図の場合、自分にかかる『重力』と床からの『垂直抗力』の大きさがつりあっているというわけですね!

→1kg=約10Nと覚えておくと便利です。
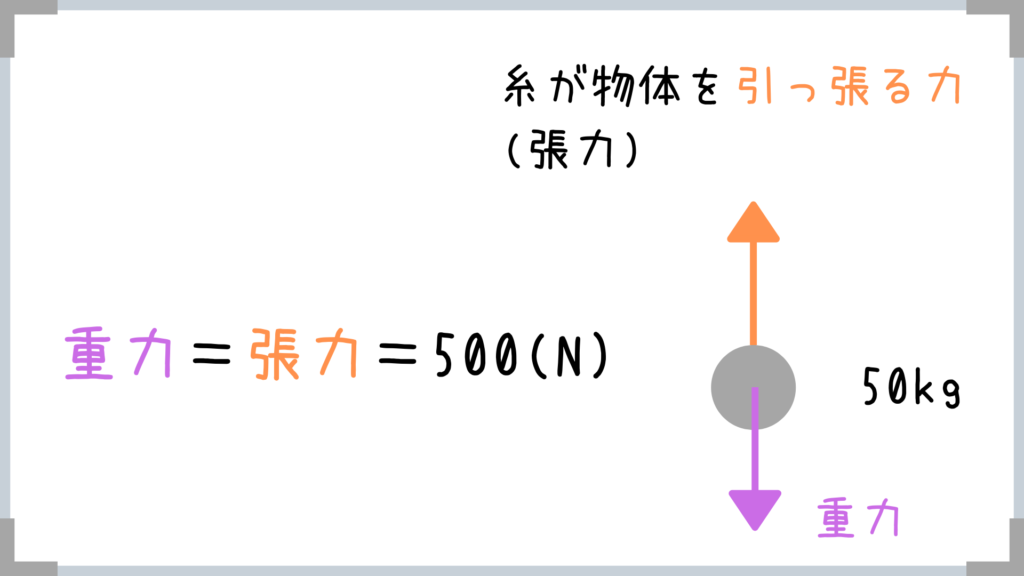
計算は省略します。
糸が出てきたりぶら下がっているものが出てきたときには『張力』という、物体を引っ張る力が作用します!
基本的にはスー過去に沿って紹介しますが、次は『摩擦力』について解説していたいと思います!

【摩擦力(力の分解)】三角関数を使わずに力を分解する!
物体と接触する面が物体の運動を妨げようとして及ぼす力のこと…なんですが、コレは皆さんイメージできる方が多いのではないでしょうか。
ぐちぐち説明する前に、基礎問題を1問解いてみましょうか!
この問題を解きながらポイントを紹介していきたいと思います!
ちなみに、この問題は超大事なので、皆さん頑張って理解していただければと思います。
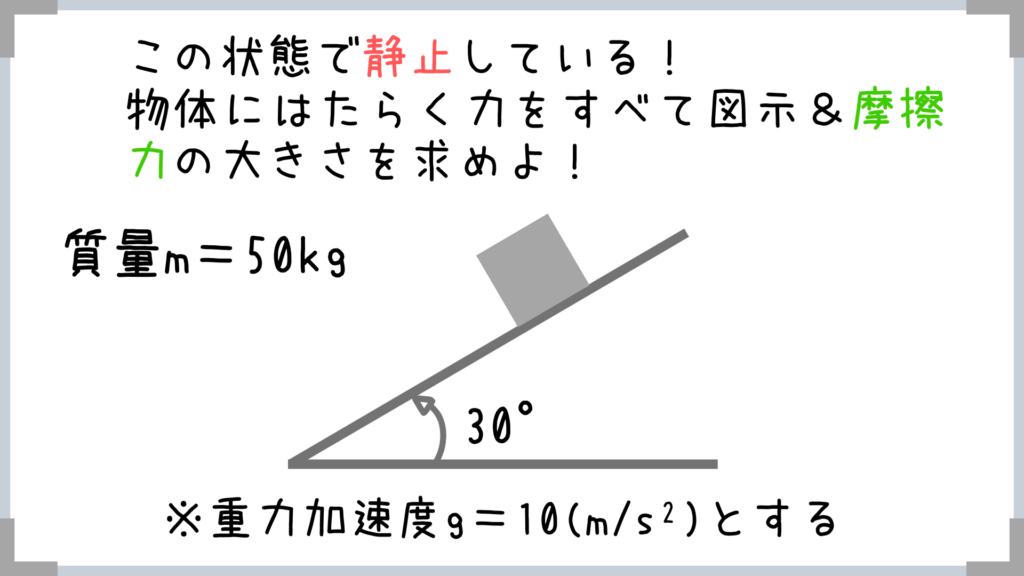
まずは物体にはたらく力を図示…
もうわけわかりませんよね(汗)
ということでポイントを紹介!
- 重力は下向き(鉛直方向)に作用
→地球の中心に向かって作用 - 垂直抗力は面に対して垂直に作用
- 「静止」している
→力が釣り合っている!
→摩擦力が発生!
さぁ実際に書き込んでみましょう!
…わからなかったら
自分が物体になって考えてみる!
この考え方を大事にしてください(笑)
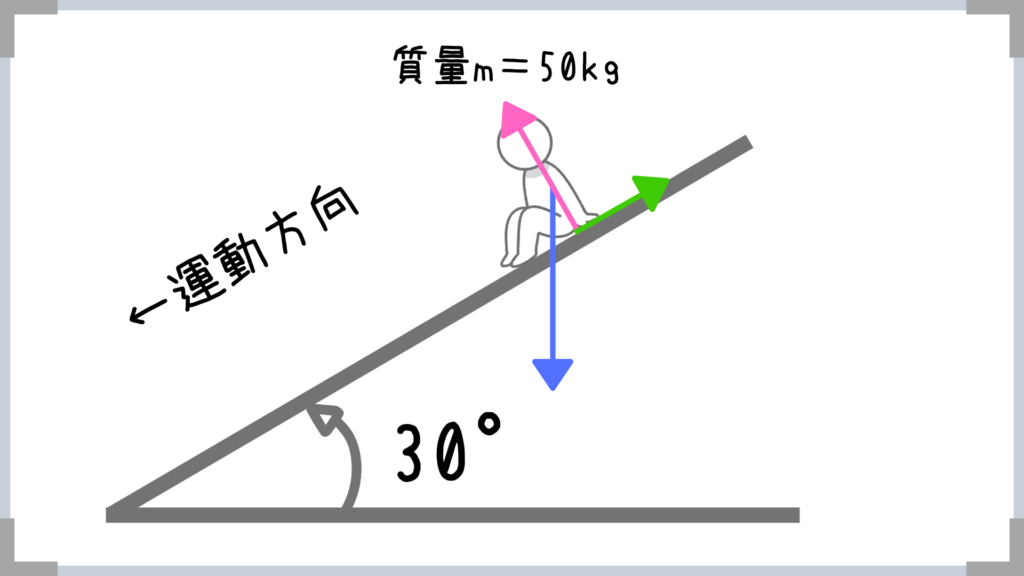
ポイントでも紹介しましたが、垂直抗力は面に対して垂直に作用するので、この点注意が必要です!
そして、自分が図の滑り台のような状態になった時に下(運動方向)に滑り落ちずに「静止している」ということは、力がつりあっているということですよね!
摩擦力というのは、
「物体と接触する面が物体の運動を妨げようとして及ぼす力のこと」
→実際に自分のお尻あたりから右上方向(運動方向の反対)に向かって摩擦力が発生しているハズです!
これで図示は完璧ですね!
そして、この図を見れば一目瞭然ですが、3つの力が釣り合っているということになりますよね。
力の大きさを求めるときは、タテ・ヨコにはたらく力をそれぞれわけて考えるのが一般的です。
タテはタテ同士で力が釣り合っている、ヨコはヨコ同士で力が釣り合っているということですね!
→タテとヨコ方向に力の向きを統一する(ここが難しい)
ココで物理の基本的な考え方『力の分解(超重要)』を行います!
図をパッと見ると、垂直抗力と摩擦力はタテとヨコ関係(直角)にありますよね!
→重力を分解するのが手っ取り早そうです。
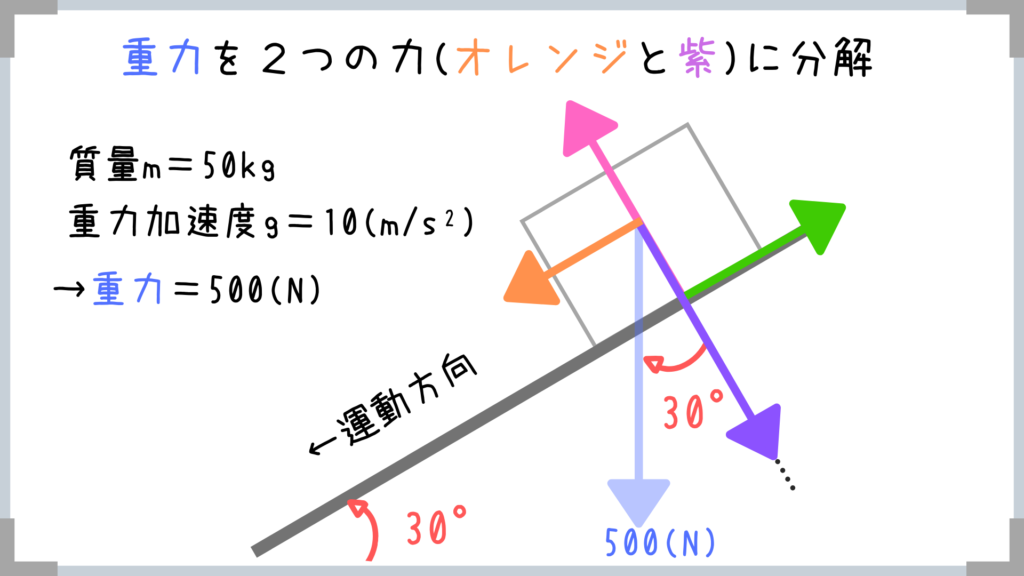
重力の大きさは最初に求めておくと後でラクです。
→W=mg=50×10=500N
そして、図のように重力(500N)をオレンジの力と紫の力にわけたいわけですよね!
ココで迷ってしまいがちなのが、「Θ(角度)ってどことどこが等しくなるんだろう…」という点なんじゃないでしょうか。
(↑の図ではすでに記載してありますが、試験本番では迷ってしまいがちです)
角度Θは図の赤色部分(↑30°)が等しくなります!
→わからなければ極端な例を書いてみましょう!
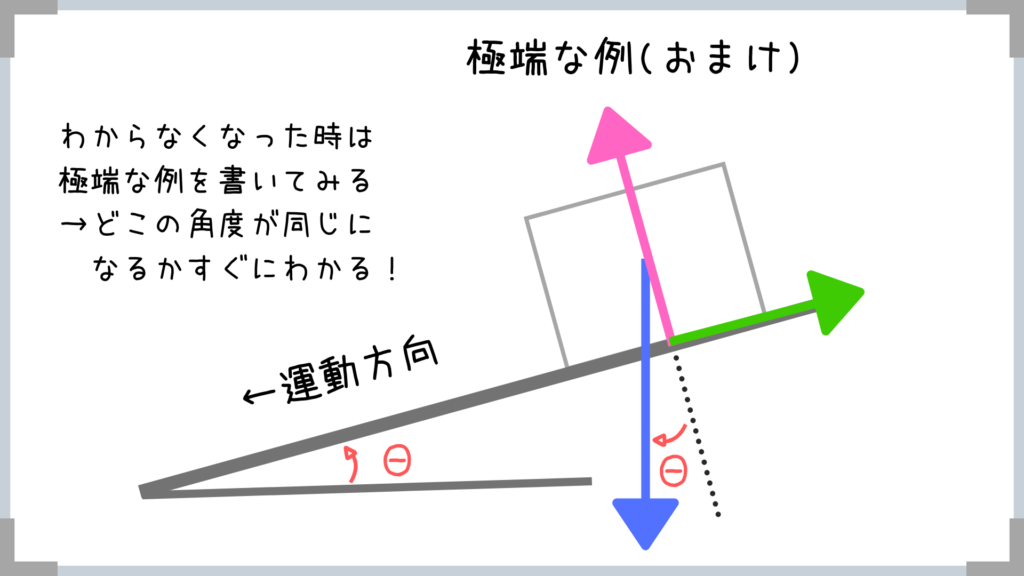
このように極端な例を書けば、
「あ~ココとココが同じ角度になるんだっけな」
ってすぐにわかると思います。
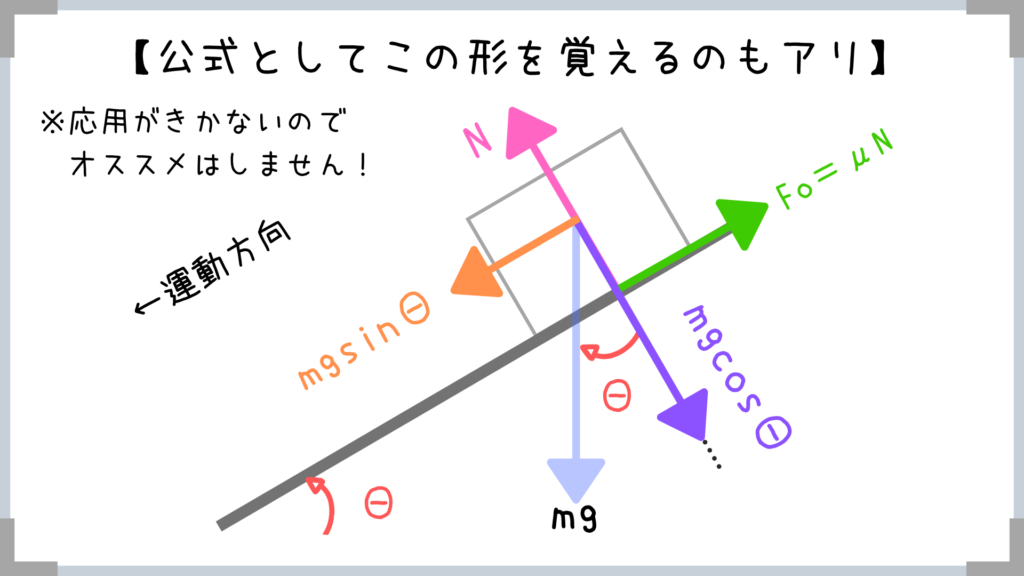 ※慣れるとこの公式の方がラクなんですけどね…(笑)
※慣れるとこの公式の方がラクなんですけどね…(笑)
では実際にオレンジの力と紫の力の大きさを求めていきたいと思いますが、実はコレは公式があります。
- オレンジの力=mg×sinΘ
- 紫の力=mg×cosΘ
この公式を使って解くのももちろんアリなのですが、
公務員試験を受ける方というのは文系の方が多いので、
「三角関数は使いたくない」
と思っている方が多いのではないでしょうか。
なるべく計算ではなく「知識」で攻めたいですよね!
そんな皆さんのために、
「知識」だけでできる『力の分解』のやり方を紹介しようと思います。
以下の2つのポイントをおさえてパターン化させていきましょう!
- 分解の仕方をパターン化しておく
→左下にΘ部分、右下部分が90°になるように三角形を配置! - 30°60°90°が超頻出!
→三角比を暗記しておく!
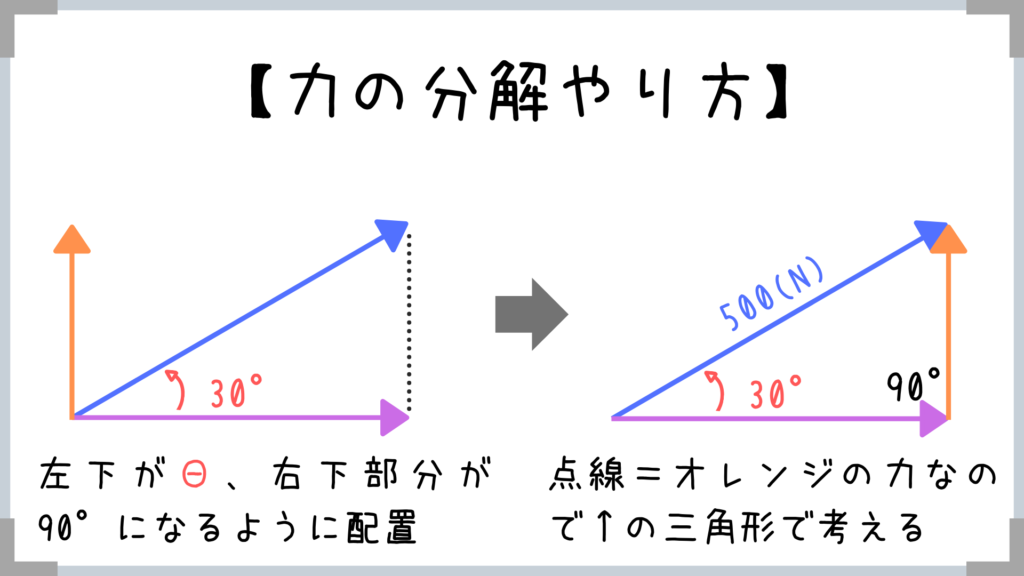
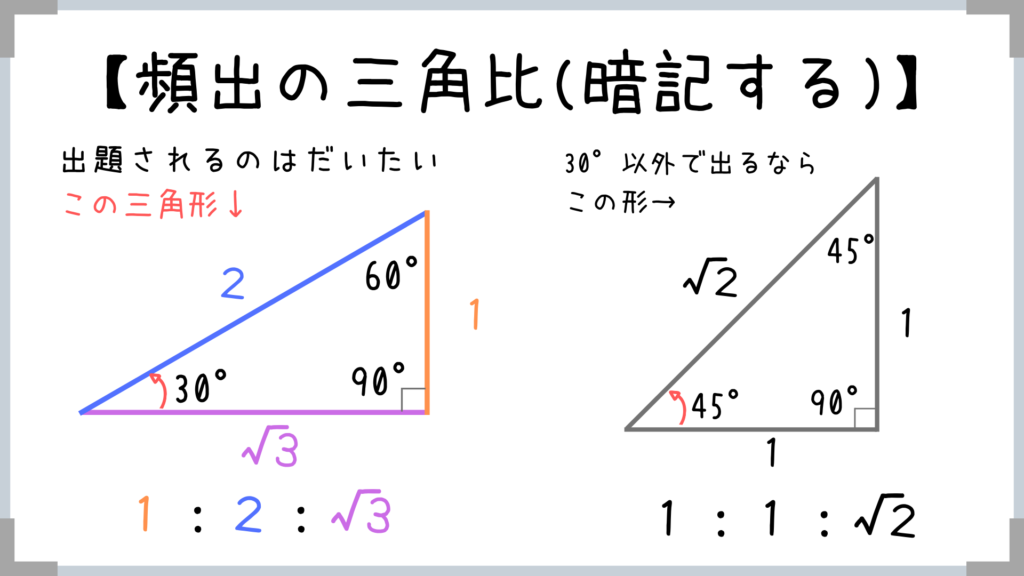
公務員試験ではこの形の三角形しか出ないと言ってもいいくらいです。
→この三角比を暗記しておけば、簡単に力を分解できる!
実際に分解してみますね!
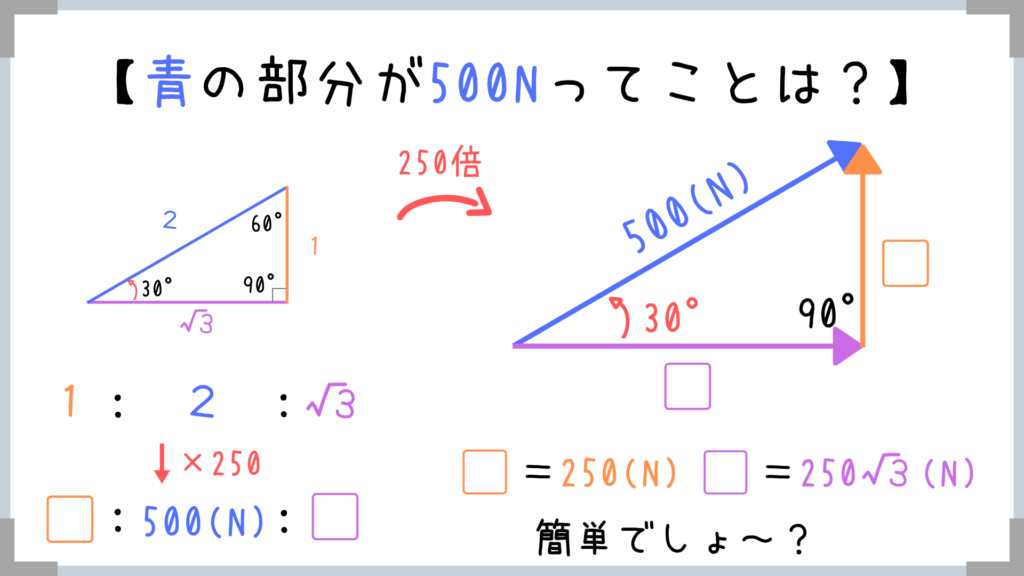
30°60°90°の三角形は公務員試験では超頻出なので、三角比は絶対に覚えておきましょう!
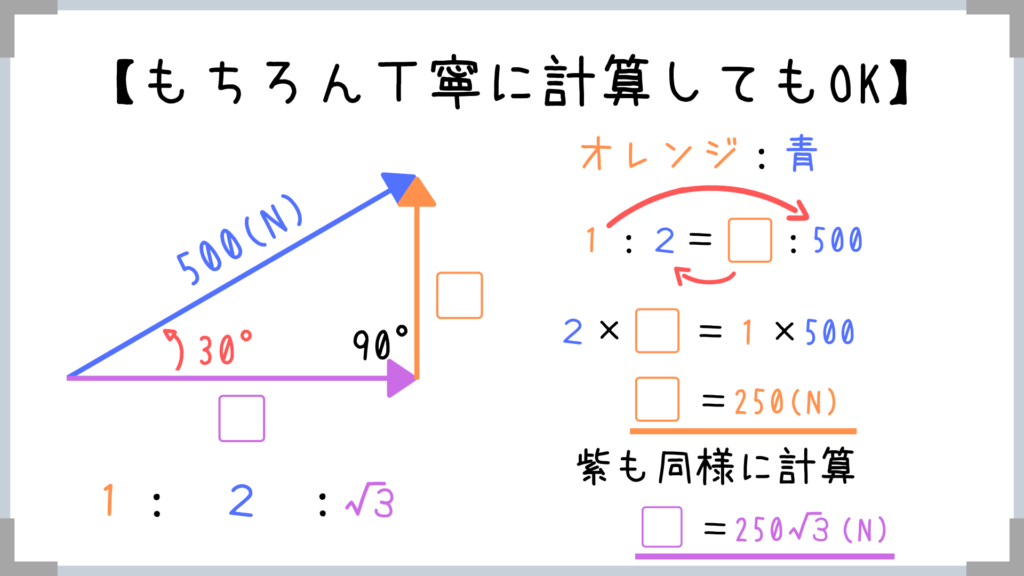
比の計算も最初は慣れないかもしれませんが、コツをつかめばあっという間にマスターできると思います!
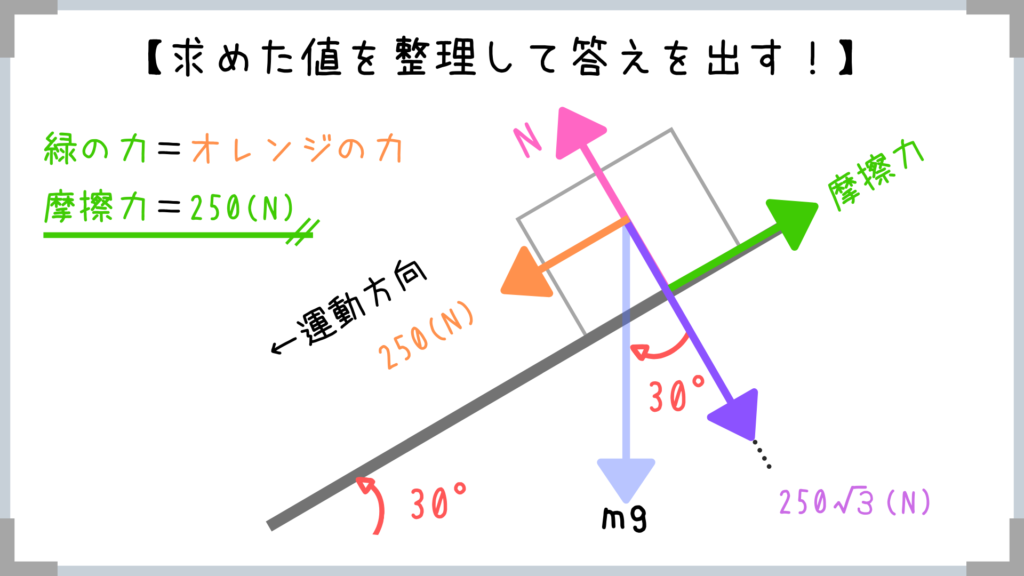
ヨコ方向(運動方向)のつり合いより、
摩擦力=オレンジの力=250Nとすぐに求まりますね!
ちなみに摩擦力(f)はf=μNとあらわせます。
(→μは摩擦係数のことですね!)
静止摩擦係数はtanΘで表され、45°で最大(μ=1)となりますが、無理に覚える必要はありません。
【力の分解】三角関数を使った分解法
一応、三角関数を使って公式に当てはめる解法も紹介しておきます。

あえてコサインから紹介!
斜辺→底辺
この流れが『C』の書き順(流れ)と同じなので、覚えやすい!
出発点が分母にくるのは確定!

斜辺→右の辺
筆記体の「s」を書くようなイメージ!
まぁこれじゃあ「へサイン」とでも言った方が覚えやすそうですけどね…
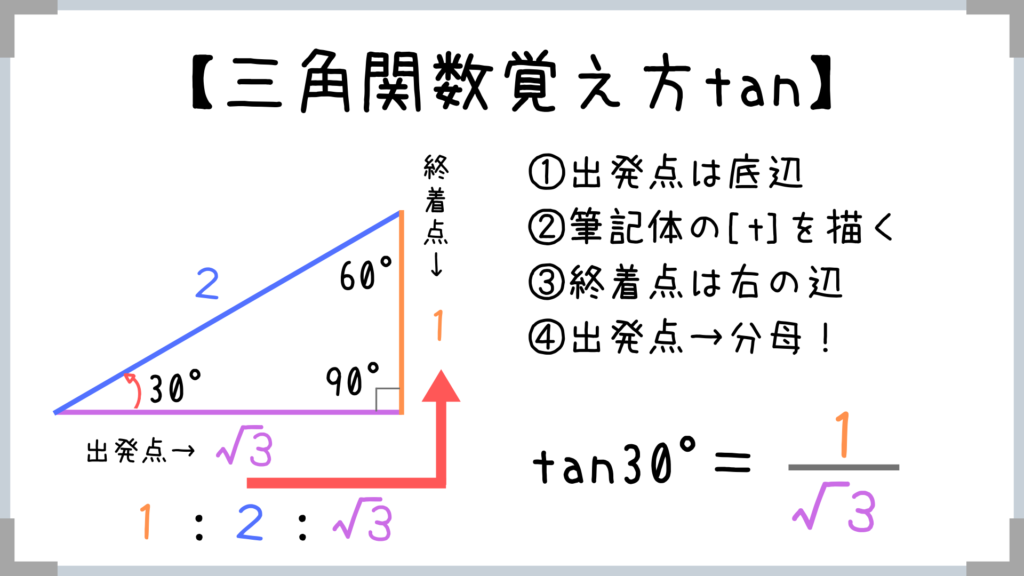
底辺→右の辺
筆記体の「t」を書くようなイメージ!
(tanはあんまり重要じゃない) まとめるとこんな感じ!
まとめるとこんな感じ!
とりあえずsinとcosだけ覚えておけばOK!

あとは公式に当てはめればすぐに答えが求まりますね!
→mg×sinΘ=500N×sin30°=500N×1/2=250N

【弾性力(ばねの合成)】フックの法則を使いこなそう!
ばねについては公式とばね定数の合成方法だけとりあえずおさえておきましょう!
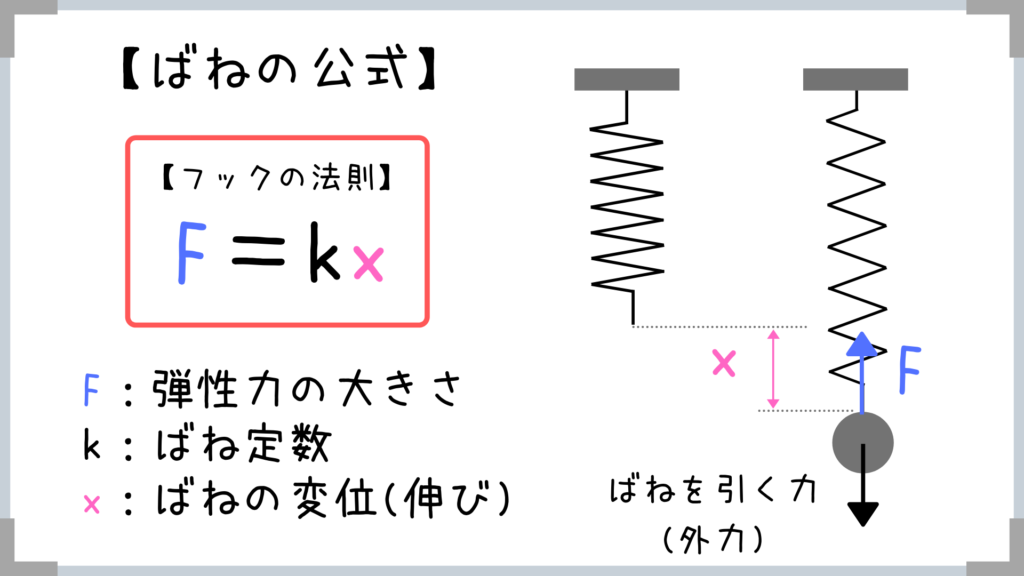
弾性力っていうのは、変形したばねなどの物体が、もとの状態に戻ろうとして物体に及ぼす力のことですね!
ばねを引っ張ったら、ばねは元の状態に戻ろうとするでしょ~?その力のことです。
例えばこの球の重さがm[kg]、重力加速度をg[m/s2]とすると
F=kx(上向き)=mg(下向き)という式が成り立つということですね!
公式は、Fが力、kが定数、xが自然長からのばねの伸び(変位)ということ!
この文字の意味をきちんと理解しておくことがめちゃくちゃ大事!

では次にばね定数の合成方法についてサクッと紹介していきます!
【ばね定数の合成方法】自分がばねになってみるのがポイント!
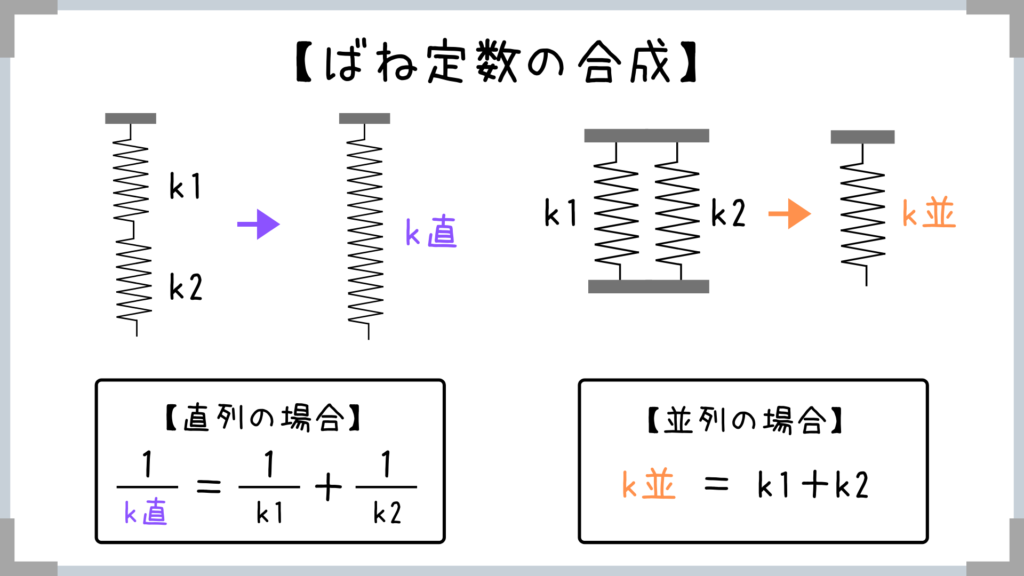
合成方法だけ覚えておけば解ける問題も過去に何問も出ているので、公式は使えるようにしておきましょう!
また、直列と並列の公式ってどっちがどっちだったか忘れてしまいがちなんですよね!
 ※ばね定数をすべてkとする。
※ばね定数をすべてkとする。
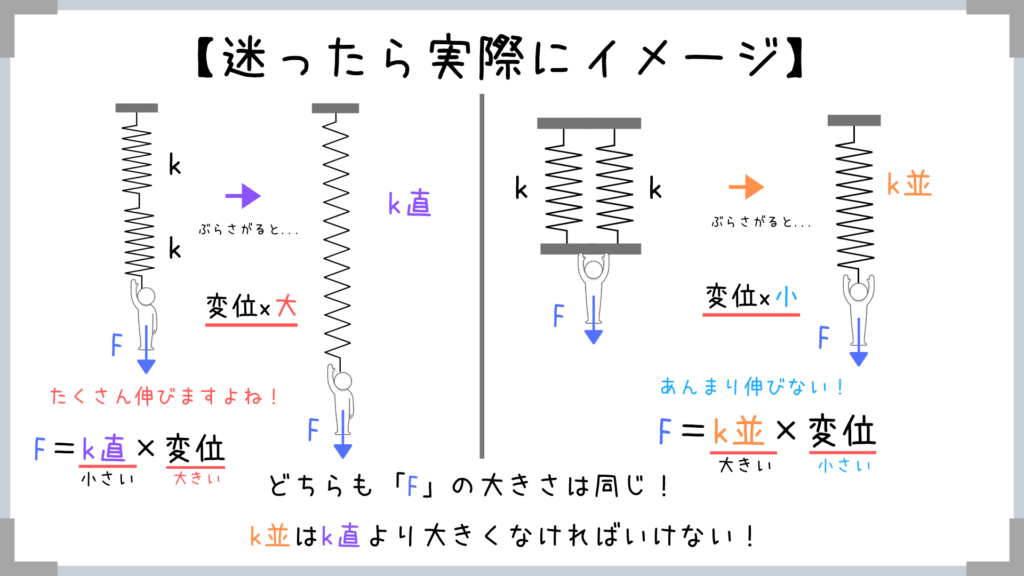
迷ったら実際に自分がばねにぶら下がってみましょう!
自分の体重は同じなので下向きはたらく力(重力)は左も右も同じです!
単純に直列のばねの方がたくさん伸びますよね?
→F=kxのx(変位)が大きいということはkは小さくなければいけない!

実際に計算してみて、k?の値が小さい方が直列、大きい方が並列ですね!
まぁコレは忘れてしまった人用の考え方なので、無理に覚える必要はありません。
公式は簡単に使えるので、コレは覚えておくようにしましょう!
【ばねの合成】実際の問題を1問解いてみよう!

実際に国税・労基の試験で出題された問題です。
だらだら問題文が書いてありますが、「ばね定数が20[N/m]のものと30[N/m]のものを合成すると?」って聞いているだけです。
公式に当てはめるだけなので図では紹介しませんが、一応丁寧に計算↓しておきました。
1/k=1/k1+1/k2
→ 1/k=1/20+1/30
→ 1/k=5/60
→ k=12[N/m]
【浮力(と圧力)】公式(アルキメデスの原理)の使い方をマスターしよう!

ちょっと理解が難しいかもしれないですが、簡単に解説!
まずはポイントから紹介。
- 単位に着目する
- 質量m[kg]=物体の密度[kg/m3]×体積[m3]を意識する!
→m(質量)=ρ物体Vという意味 - 浮力=重力→つりあっている(静止)
(ρ流体gV=mg=ρ物体Vg)
問題にはだいたい「物体の密度」と「流体の密度」が出てくるので、ここの意味を履き違えないように注意が必要です!
また、重力を求める際は、「物体の体積」を使用しますが、浮力を求める際は「流体に触れている部分の体積」を使用します!
→ここら辺の公式の使い方は演習問題等で慣れる必要がある!(そんなに難しくない)

物体の密度に体積をかけたら物体の質量がでますよね?
重力はmgで(質量×重力加速度)これが下向きにはたらいています。
このように単純に考えればOK!
ではポイントを踏まえて簡単な問題(例題)を1問やってみましょう!
【浮力の例題】風船は浮く?沈む?静止する…?

公式の使い方を理解していれば一発ですね~!
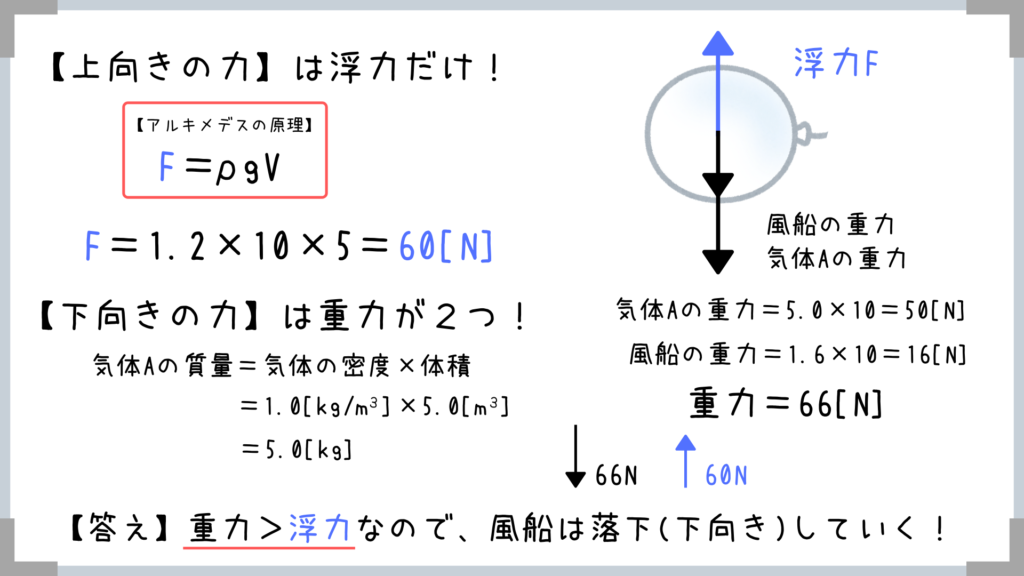
なんとなく浮力の公式の使い方がわかってきましたか~?
水に物体を浮かばせる問題もたまにでるので、もう1問解説しておきますね!
【浮力の演習問題】実はココの体積が等しい!
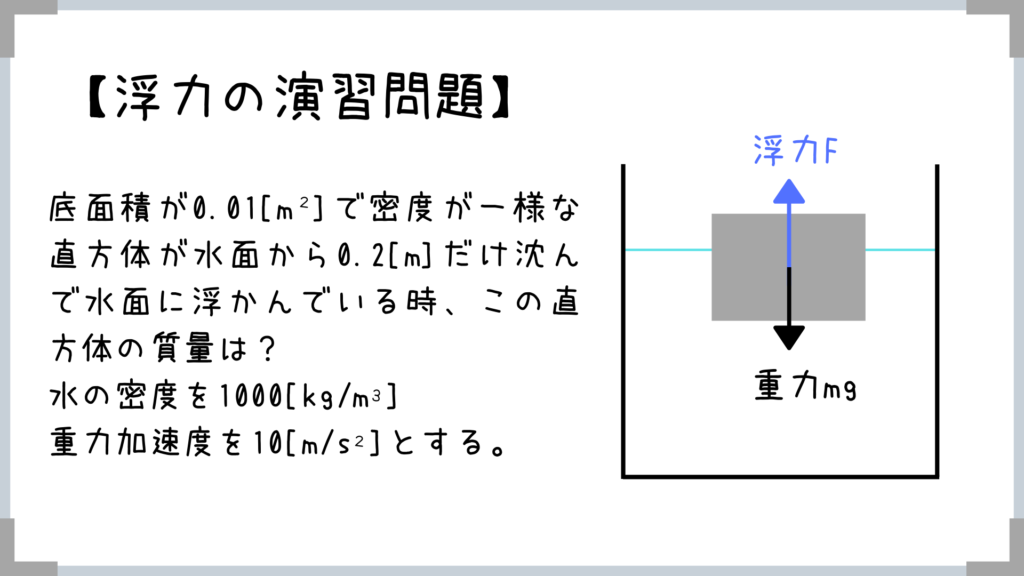
物体が流体を排除した部分(水に浸っている部分)の体積って、実は水位が上がった分の水の体積と同じ量なんですね。
→水位があがっが分の水の重さが浮力となります。
(細かい話は覚えなくても、問題が解ければOK)
要は公式のρgVに↓これらの値を代入して、浮力=重力の式を作ればOK!
ρ:水の密度
g:重力加速度
V:水面下の直方体の体積
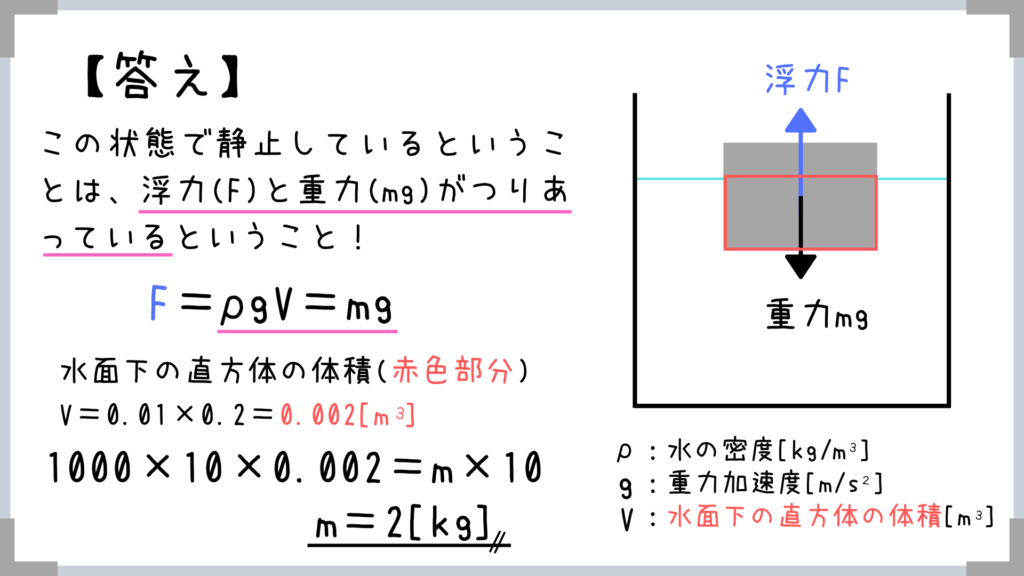
浮力の公式の考え方として、体積の扱い方に注意が必要!
水面下の部分の体積を公式に当てはめます!
はじめて浮力について勉強する方は、慣れるまで少し時間がかかるかもしれませんね。
【圧力】1Pa(パスカル)って?
圧力って言うのは、1[m2](単位体積)あたりの面を垂直に押す力のことですね!
そして1Paというのは、1[N/m2]のこと…
なんですが、大事なのはイメージすること!
ということで圧力についても実際にイメージしてみましょう!
 1Paについてもっと細かく言うと、1cmあたりに0.01グラムの力が加わっているくらいですね!
1Paについてもっと細かく言うと、1cmあたりに0.01グラムの力が加わっているくらいですね!
圧力についてなんとなくイメージできましたか?
ちなみに、流体中で物体が受ける浮力の大きさは、流体の圧力を物体の全表面にわたって合計したものですね。
(変に覚える必要はない、公式が使いこなせればOK)
ということで演習問題を1問解いてみましょう!

圧力の単位は[N/m2]
【圧力の演習問題】まさかCが答えなんて言いませんよね~!
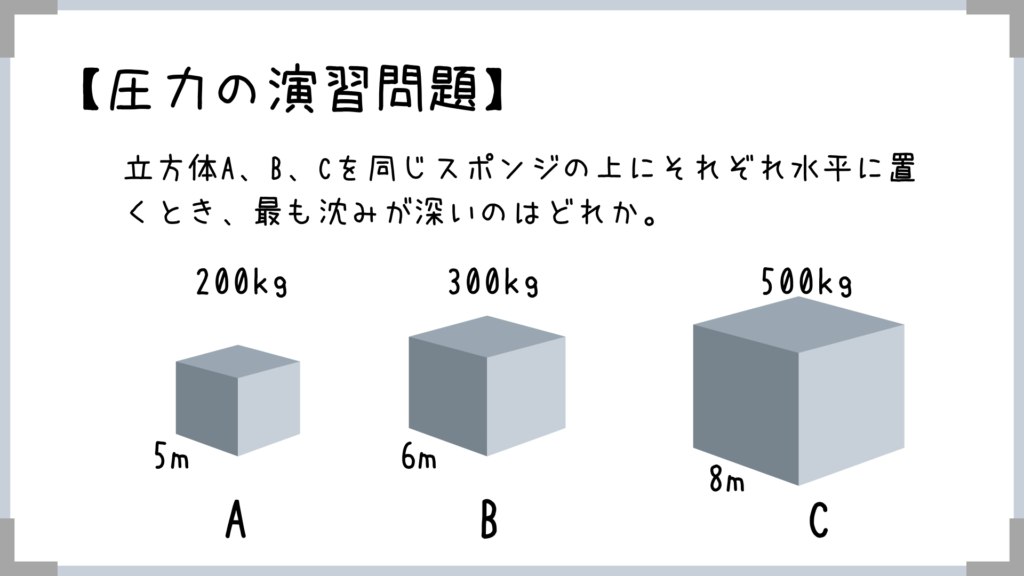
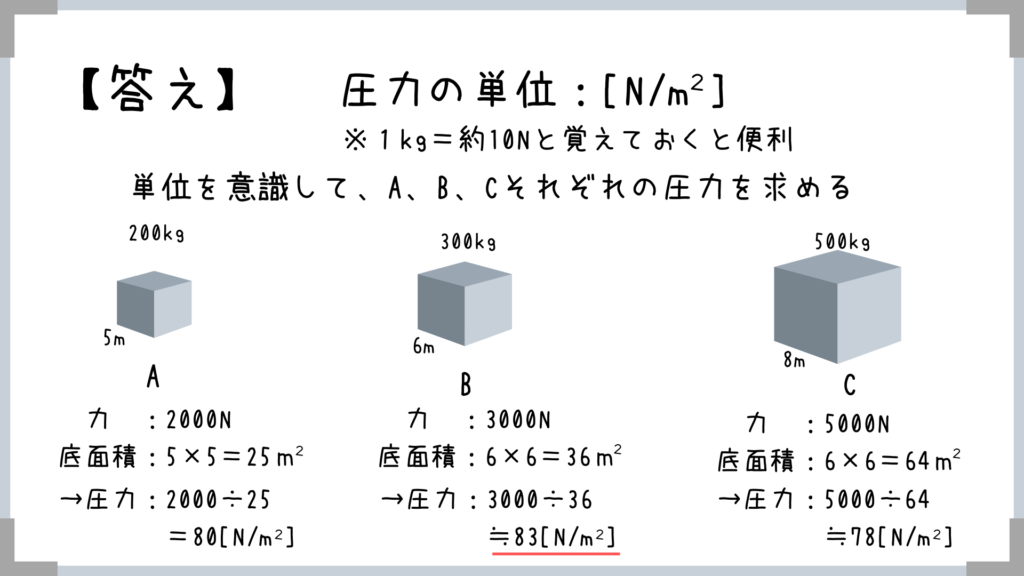
ものの大きさが圧力に直結するわけではないですよね!
同じ力でも、底面積が小さけれ力はその面に集中してはたらきますからね!
【3力のつりあい】力の分解をマスターすれば超簡単に解けちゃう!
実際に問題を解いて感覚を身に着けていきましょう!

問題が出たらまずは図示する、コレは鉄則!
そして、どんな力がはたらくかわからなくなったら
自分が物体になる!
これも鉄則(せんせい流)
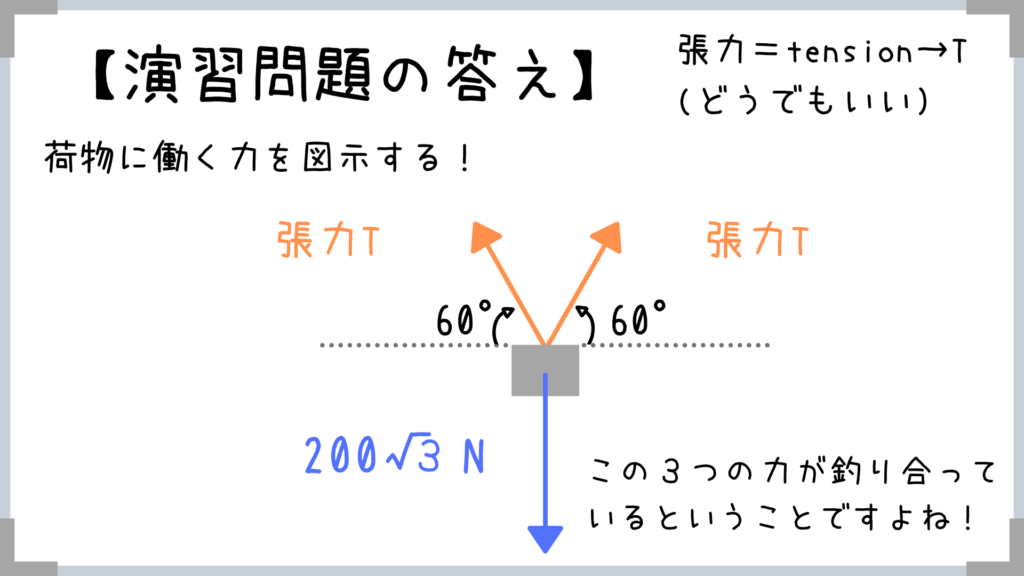
物体の重力と張力がそれぞれはたらきますよね!
基本的には斜めの力が出てきたらタテとヨコに分解します!
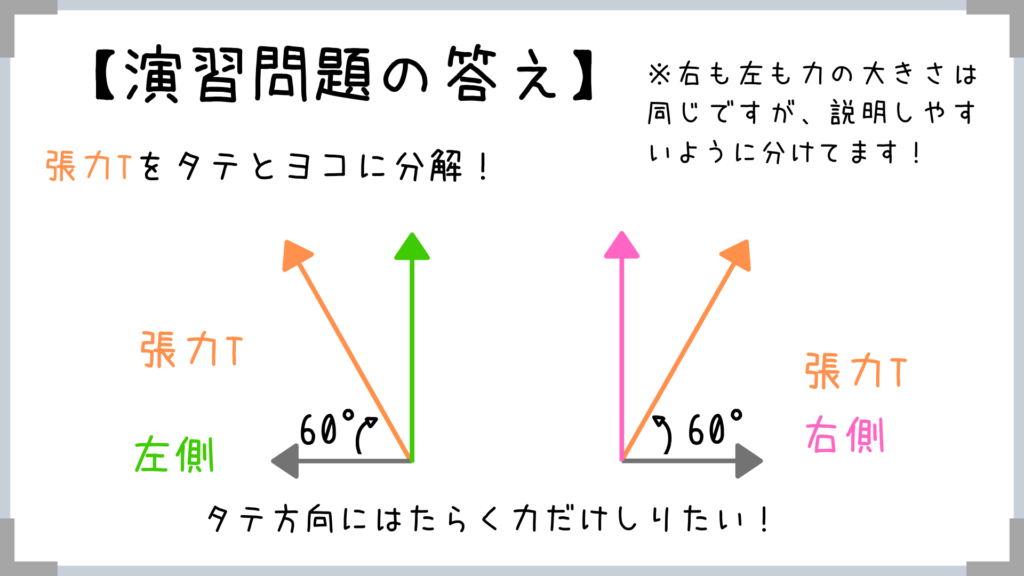
わからない文字がTだけなので、タテの力だけ求めれば答えが求められそう!
(ヨコにはたらく無駄な力を求めても仕方がない)
先ほど紹介した『三角比』の使い方をマスターしている人はすぐに緑とピンクの力が求められるハズ…!!
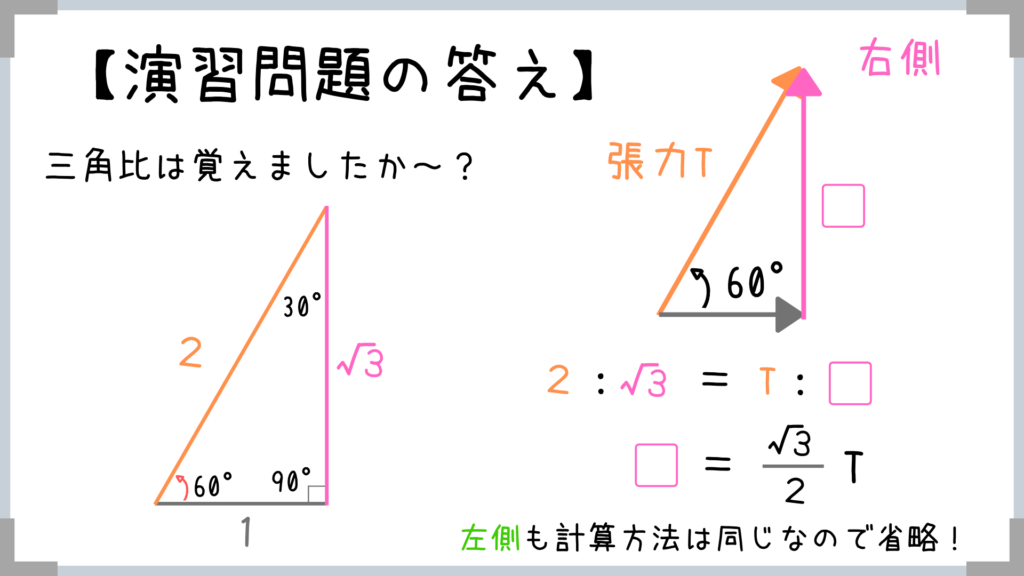
慣れてる人は
ピンクの力=T×sin60°=√3T/2
と求めてもOK!
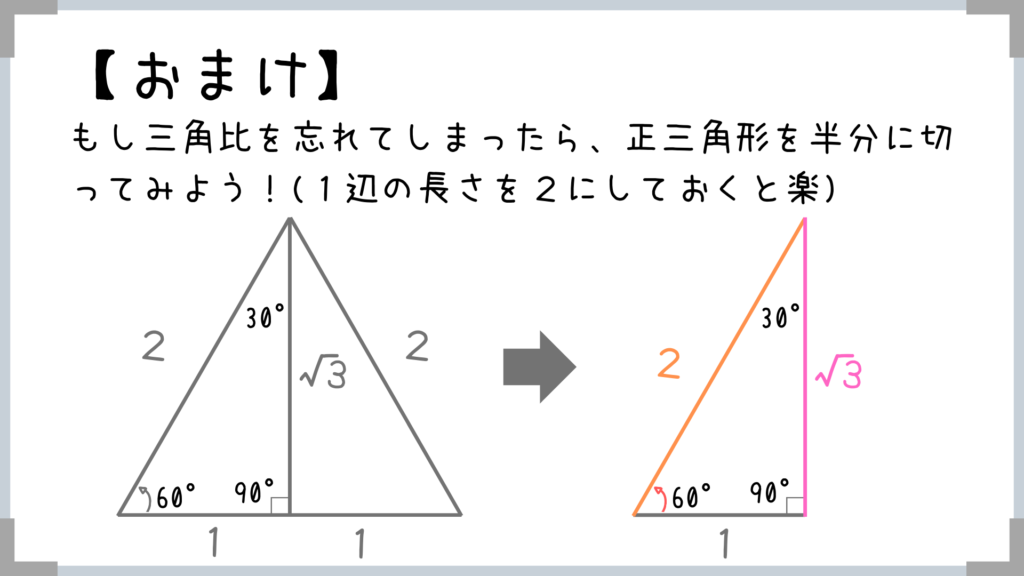
三角比を忘れちゃったら正三角形を書いて、それを半分に切って考えてみれば比をすぐに求められます(余談)
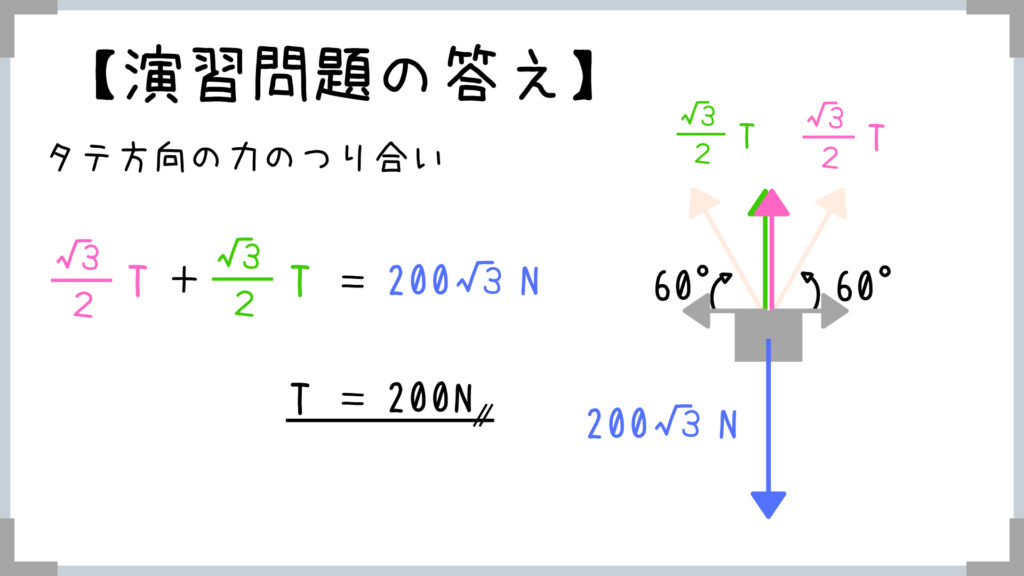
では求めた力をいったん整理して、Tの大きさを計算していきましょうか!
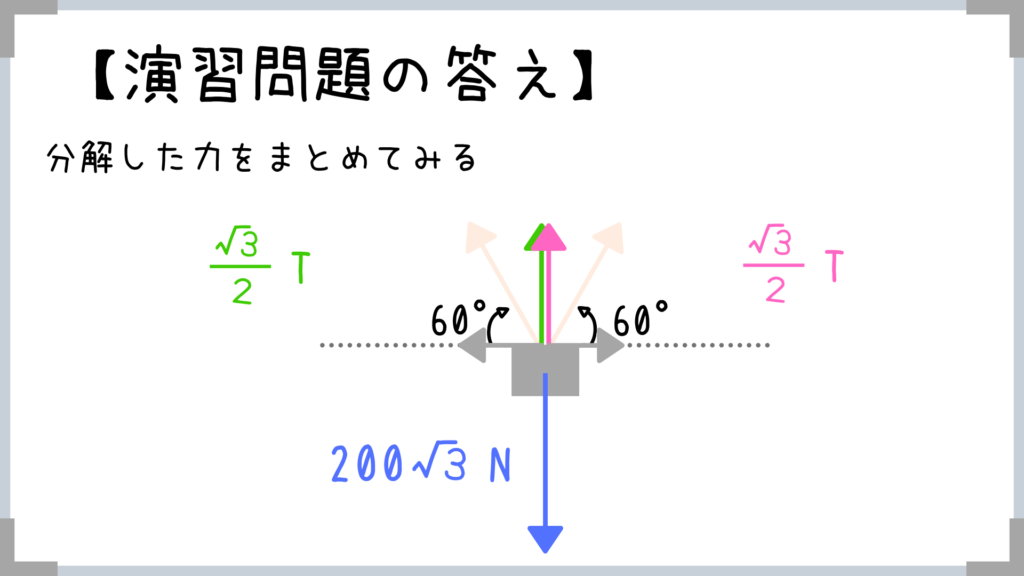
上向きの力=下向きの力
→緑の力+ピンクの力=重力

【力のモーメント(回転させる力)】苦手な方も一瞬で理解できる!
力のモーメントというとイメージがわかないので、回転させる力と私は勝手にそう呼びます(笑)
「回転させる力?」「なんじゃそりゃ」って状態だと思いますので、まずは「回転させる力」がどんなものか簡単に紹介していきたいと思います。
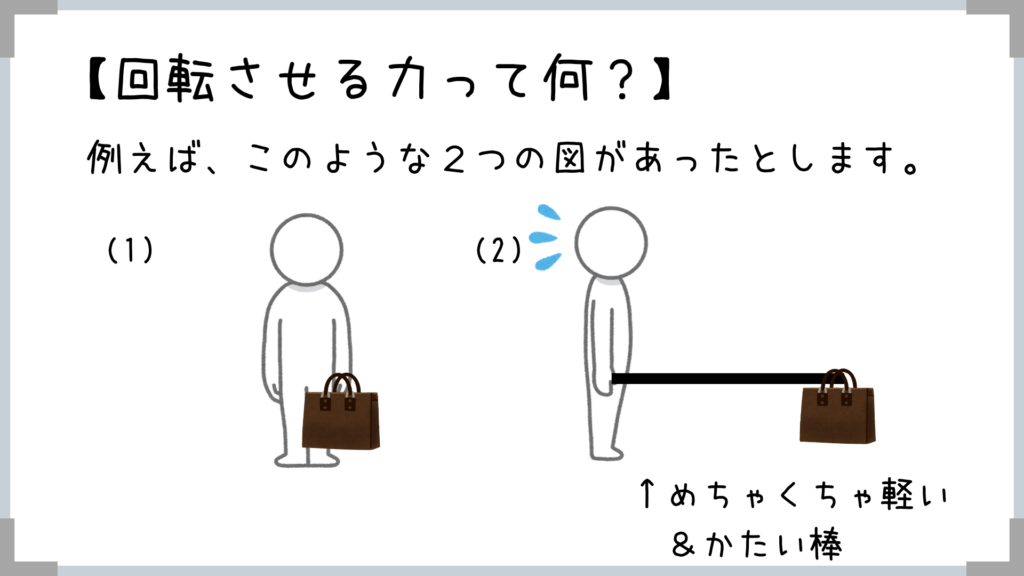
※棒の重さは無視
持っているバッグの重さは同じなのに「手(軸)」にかかる負担って同じじゃないですよね?
ココ(手)に着目してはたらく力を図示してみましょう!
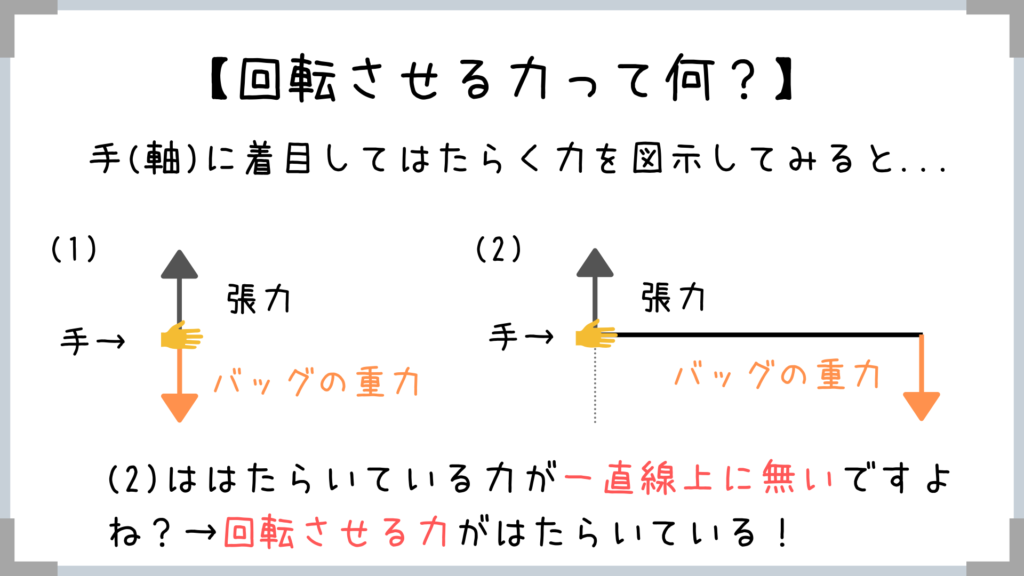 鉛直方向の力はつり合っていますよね!
鉛直方向の力はつり合っていますよね!
でも(1)は手に張力と重力がそれぞれ直接加わりますが、(2)はバッグの重力の作用点まで距離があります。
ということでポイントを紹介!
- 自分が軸(支点・物体)になってみて、その点(軸)に力が集中しているようであれば、回転させる力ははたらいていない!
- 作用点まで距離がある場合は、回転させる力がはたらいている!
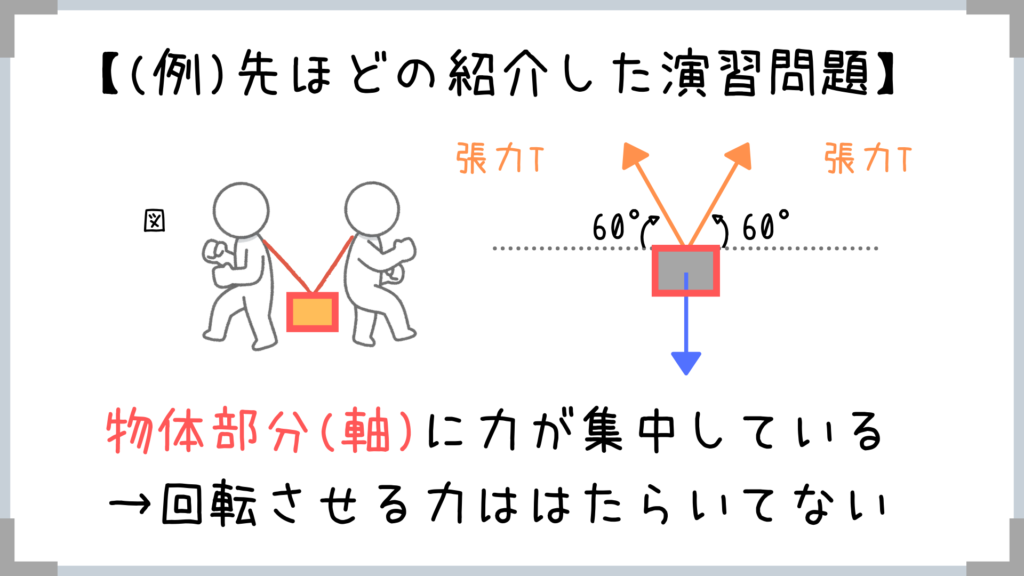
さっき紹介した3力のつりあいの問題(例)は物体部分に力が集中してますよね?
→回転させる力がはたらいていないことになります。
※この例では回転させる力がはたらいていますがつりあっています。(M=0)
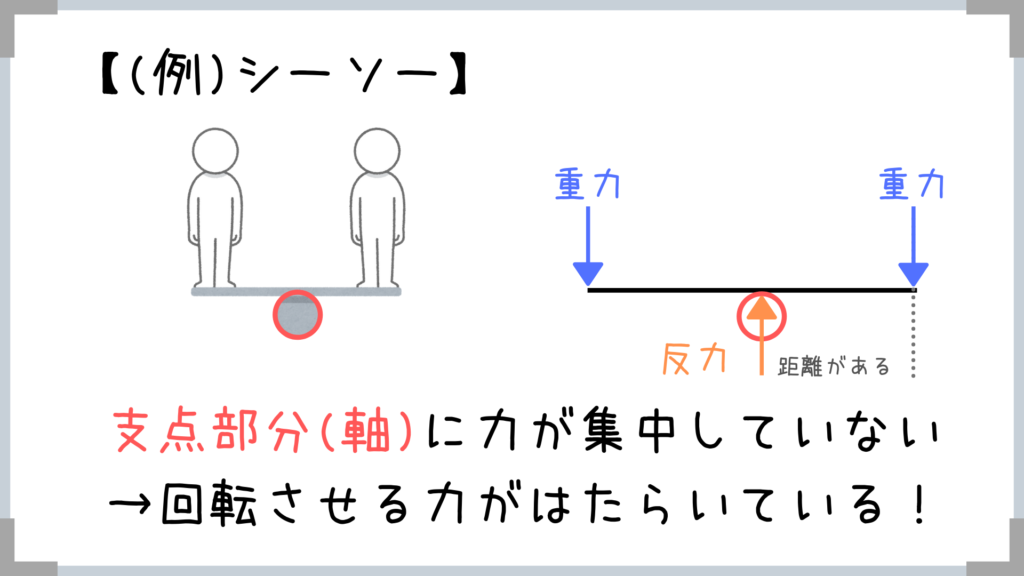
例えばシーソーなんかは、軸部分に力が集中していないですよね?
重力は鉛直下向き作用しますから、軸から作用点まで距離があります!
→回転させる力がはたらいている!
なんとなくイメージがつかめましたか?
もし慣れないようであれば、毎回回転させる力も図示しておけばOKです。
(計算するとゼロになるので必然的に消える)
次に『回転させる力の大きさ』に触れていきたいと思います。
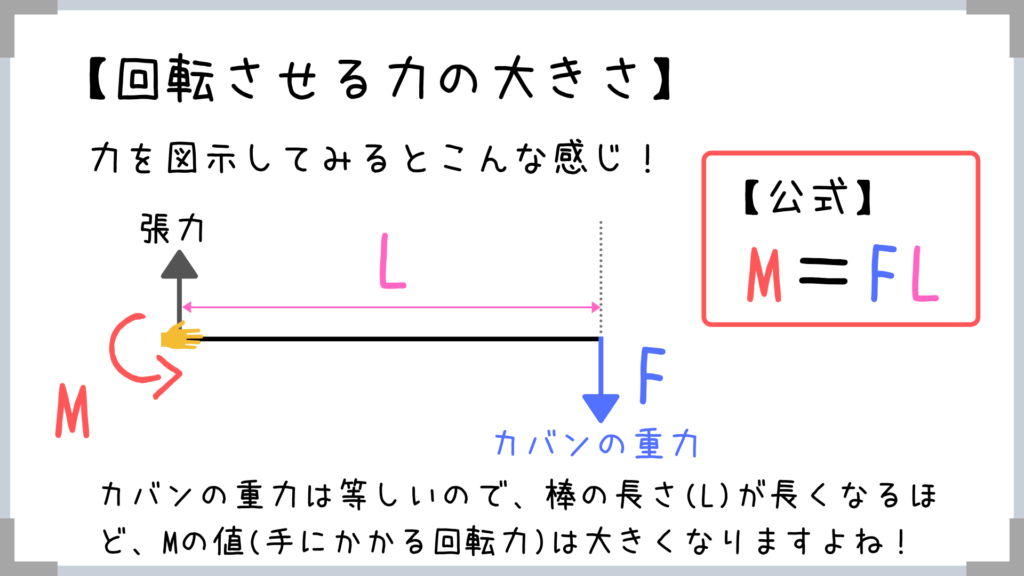
【回転させる力の大きさ】力のモーメントの公式はコレ!
回転させる力の大きさ(力のモーメント)をM、
作用する力をF
作用点まで距離をL
とすると
M=FL
とあらわせる。
 カバンが受ける重力の大きさは同じなのに、距離が遠くなるにつれて手の負担は大きくなります。
カバンが受ける重力の大きさは同じなのに、距離が遠くなるにつれて手の負担は大きくなります。
M=FLなので、L(距離)が大きくなるにつれてMも大きくなるということですね!
そして、この状態で「静止している」ということは…
「反時計回りの力=時計回りの力」
→この2つがつりあっているということです!
だから静止しているということは、「張力」「重力」のほかに「回転させる力(M)」が手の部分にはたらいているということですね!
これで基礎知識は終了。
実際に問題を解いてみましょう!
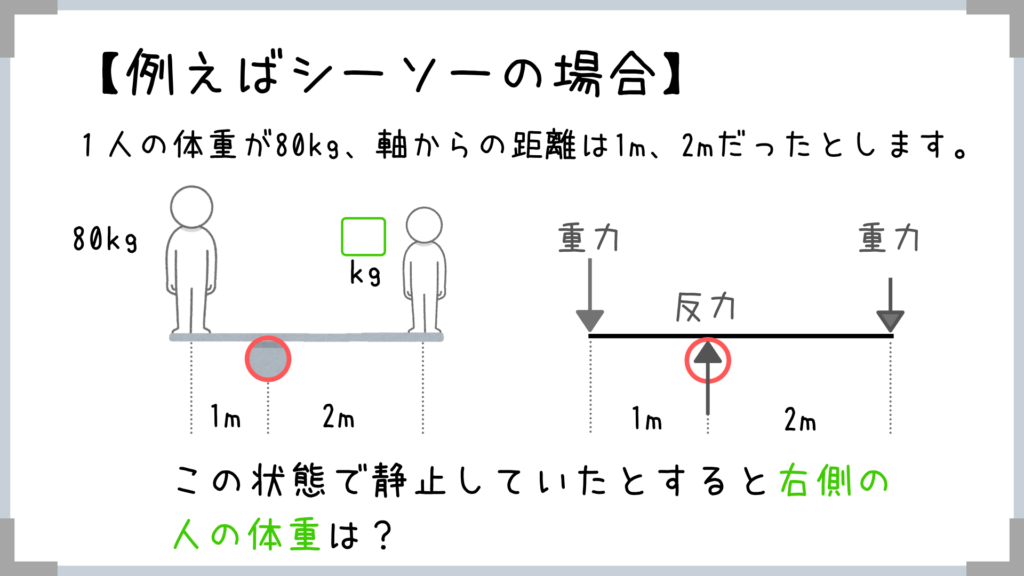
回転させる力(力のモーメント)マスターの皆さんなら余裕ですよね!

答えは40kgです。
てこの原理と同じですね。
支点、力点、作用点!
80kgの人を持ち上げるのに、40kgの人は支点ー力点間の距離を、支点ー作用点の距離の2倍にしすれば持ち上げることができるということですね!

力のモーメントに関するココまでのポイントをまとめるとこんな感じ!
あともう1点、知っておかなければいけないことがあるので紹介します!
そして、公務員試験でも最近、力のモーメントの問題は多く見かけるので、詳しめに解説していきたいと思います!
【力のモーメントの演習問題】自分が軸になることが大事!
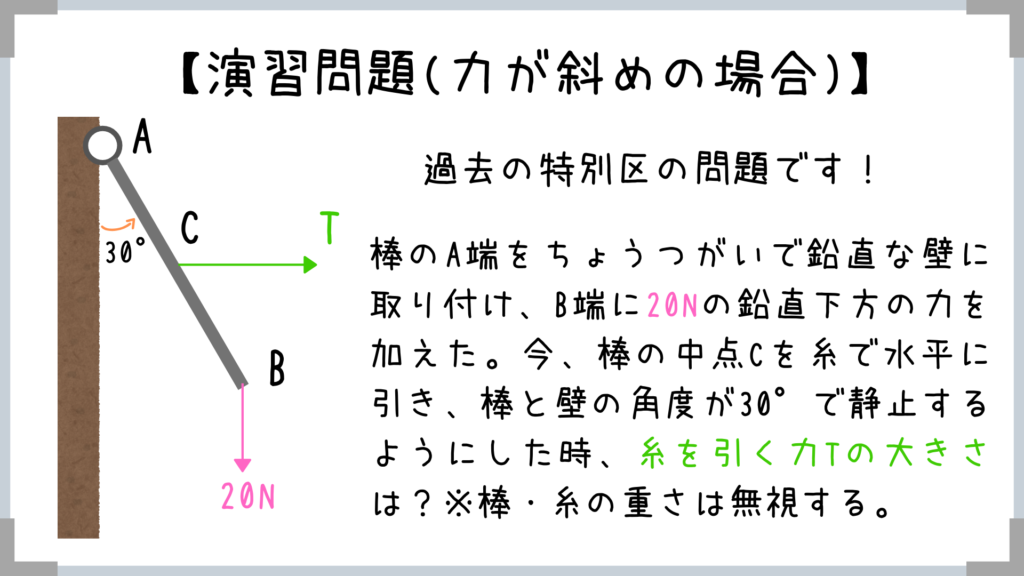
複雑そうでめちゃくちゃ難しくみえますよね?
でも、実はポイントを知っている人からすると超簡単な問題なんです。
物理で大事なのは「イメージ」すること!
ということでさっそく例を紹介。
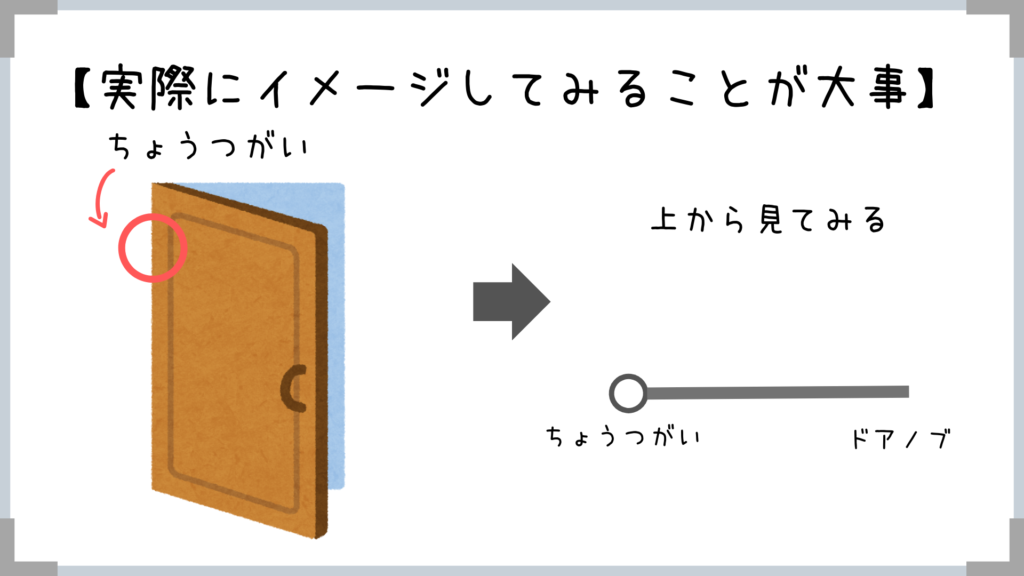
そして、自分が軸(A点)になって考えてみることが大事!
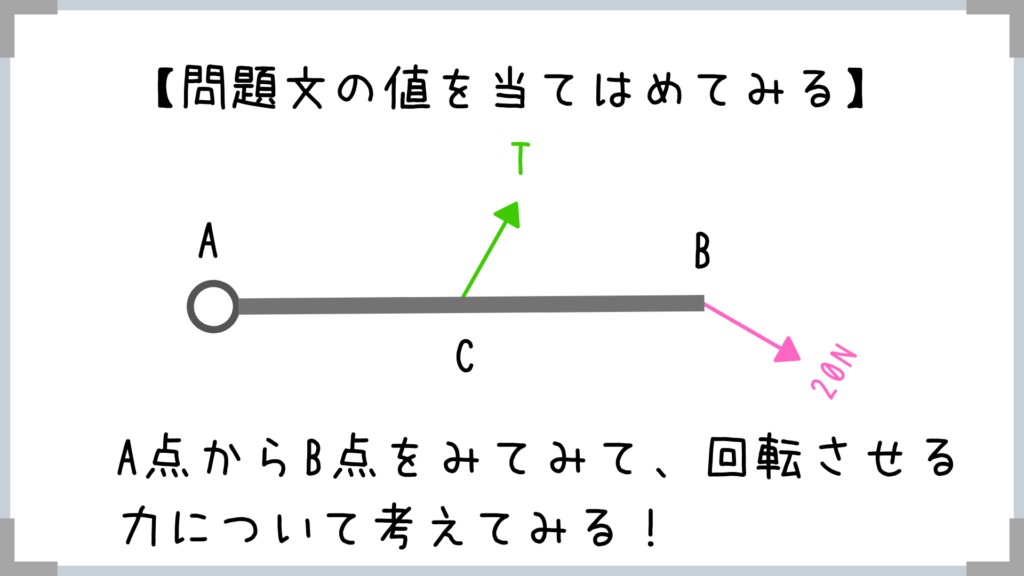
- 回転軸から力の作用点までの向きと作用する力の向きは垂直であること!
- 斜めの力はタテとヨコに分解して考える!
- 垂直にはたらく力だけが回転力に寄与
この3つのポイントをおさえて↑の問題を解いていきますよ!
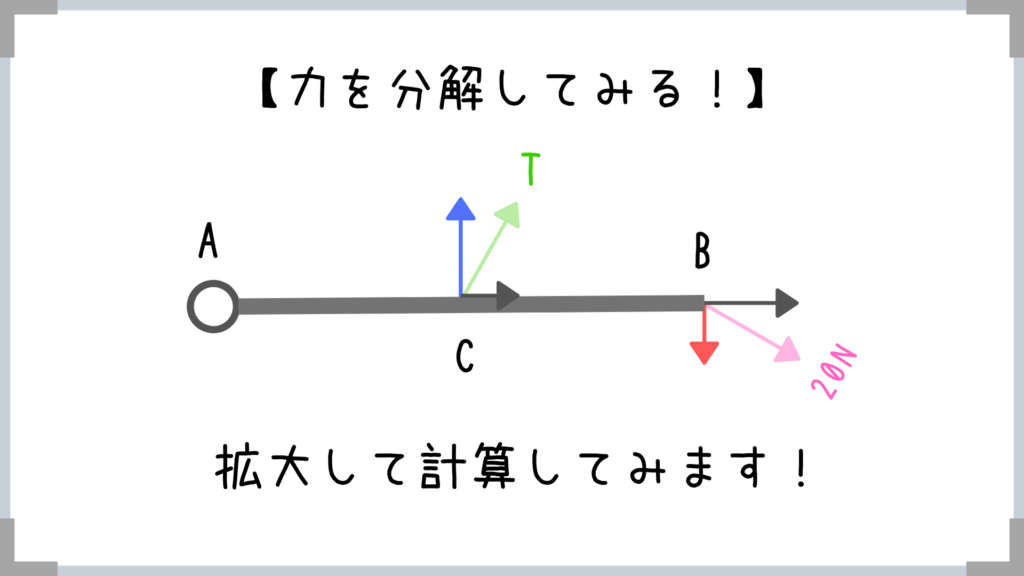
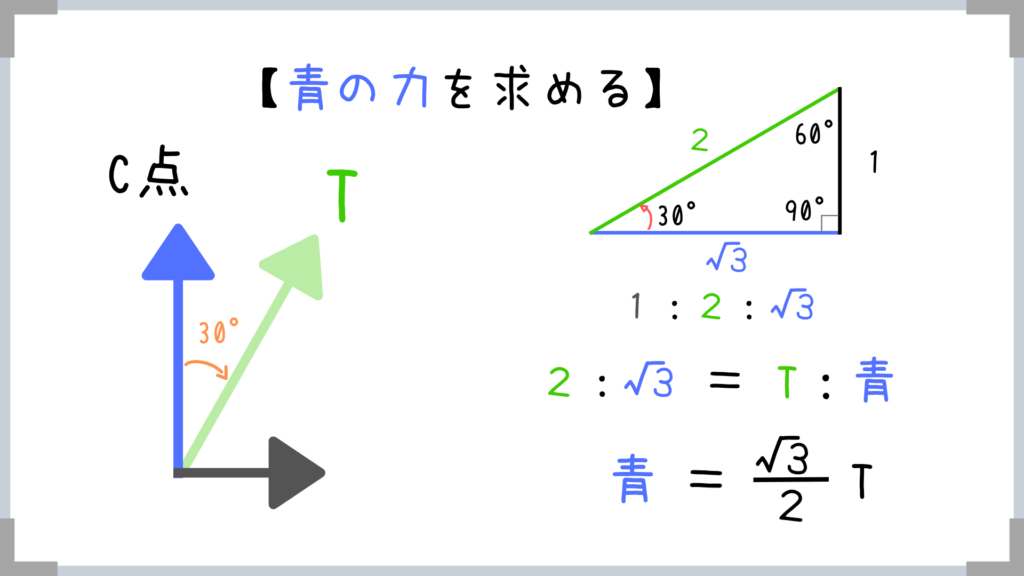
三角比の使い方は慣れてきましたか?
物理が得意な人は公式を使って
青の力=Tcos30°だからすぐに求められますね!
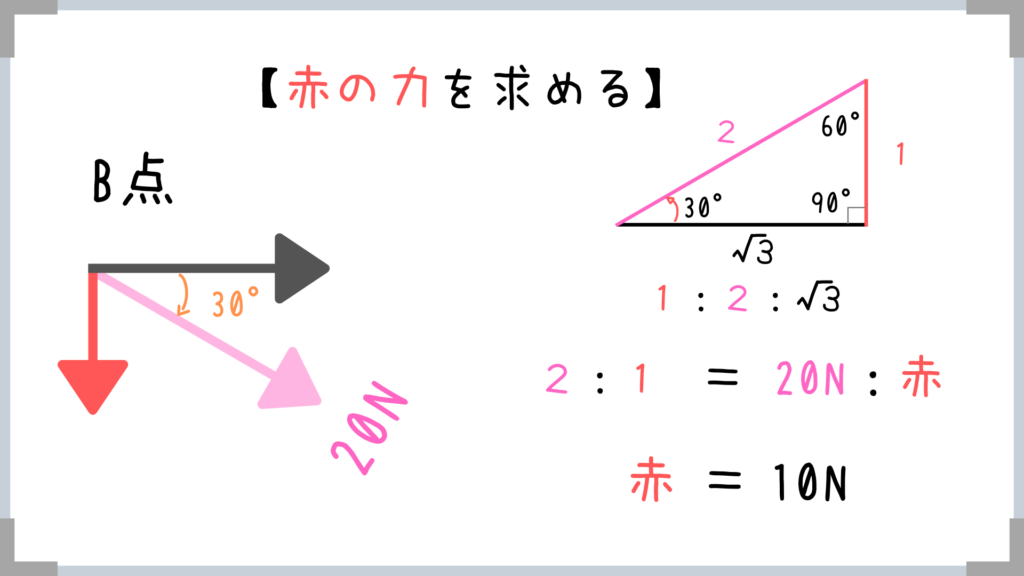
こちらも青の力と同様、三角比を使って求めてもOKですし、公式を使って20N×sin30°って求めてもOK!
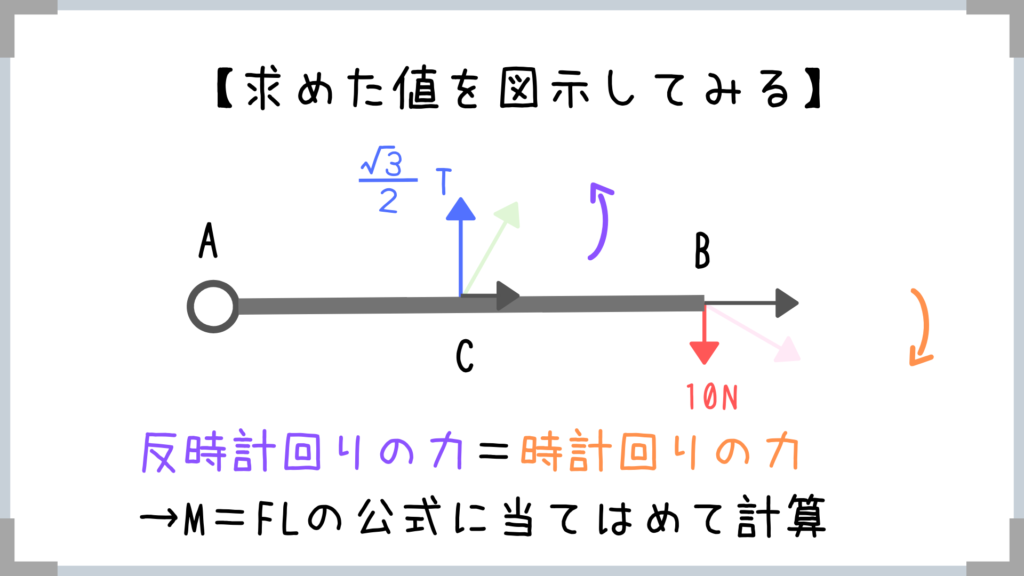
あとは計算するだけ!
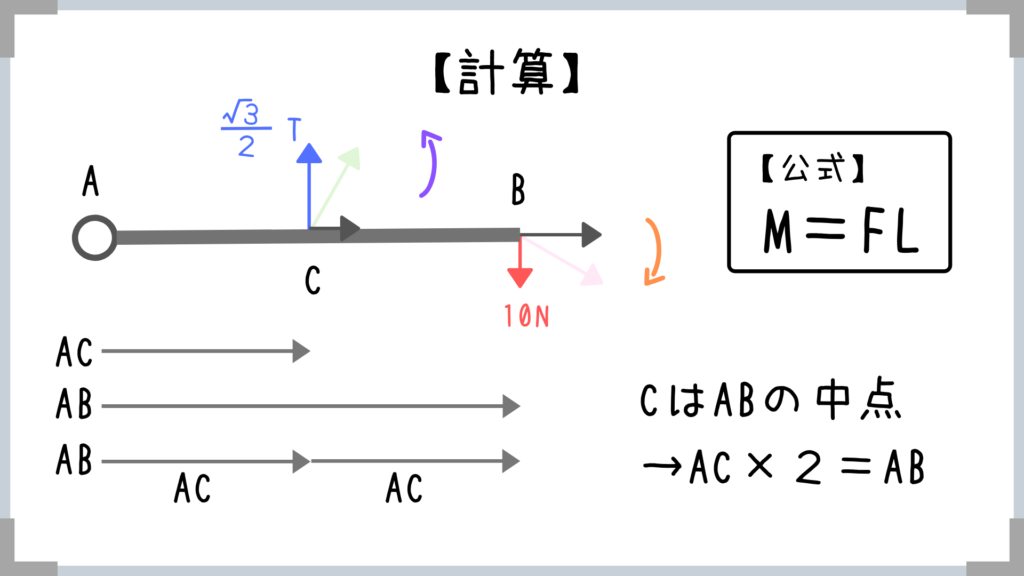

こんな感じでイメージしやすいように解法を紹介しましたが、実はもっと簡単な解法もあります。
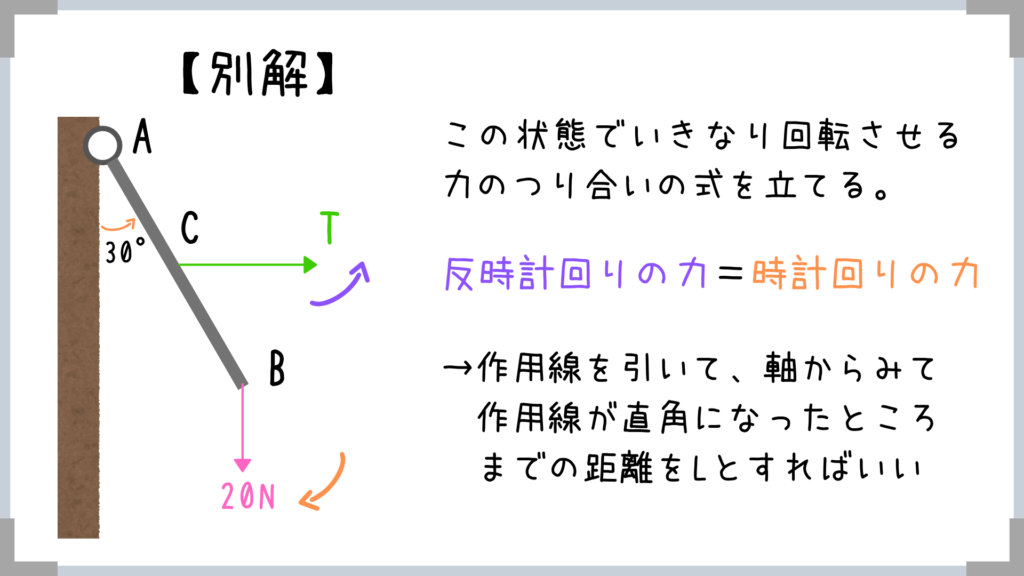
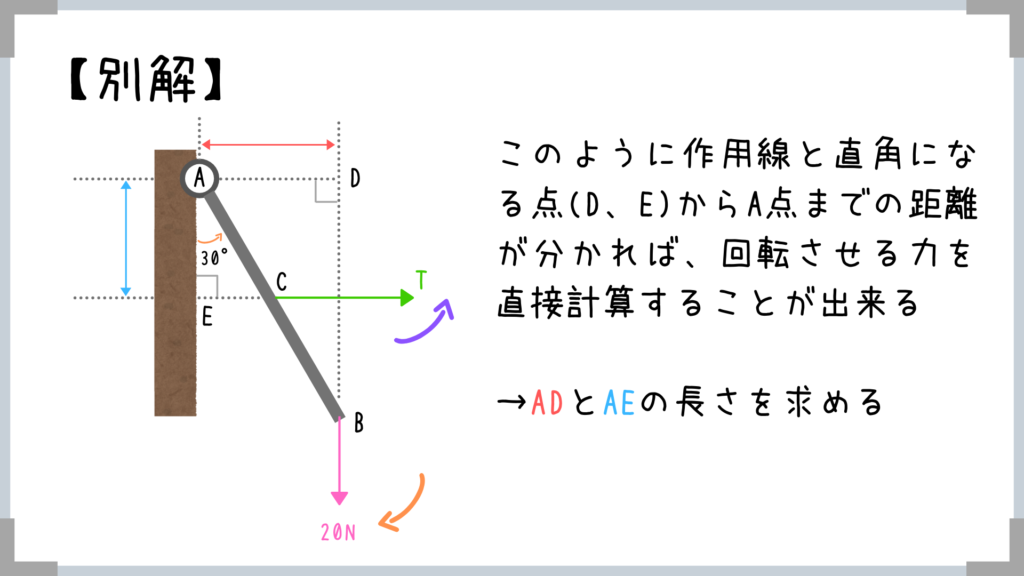
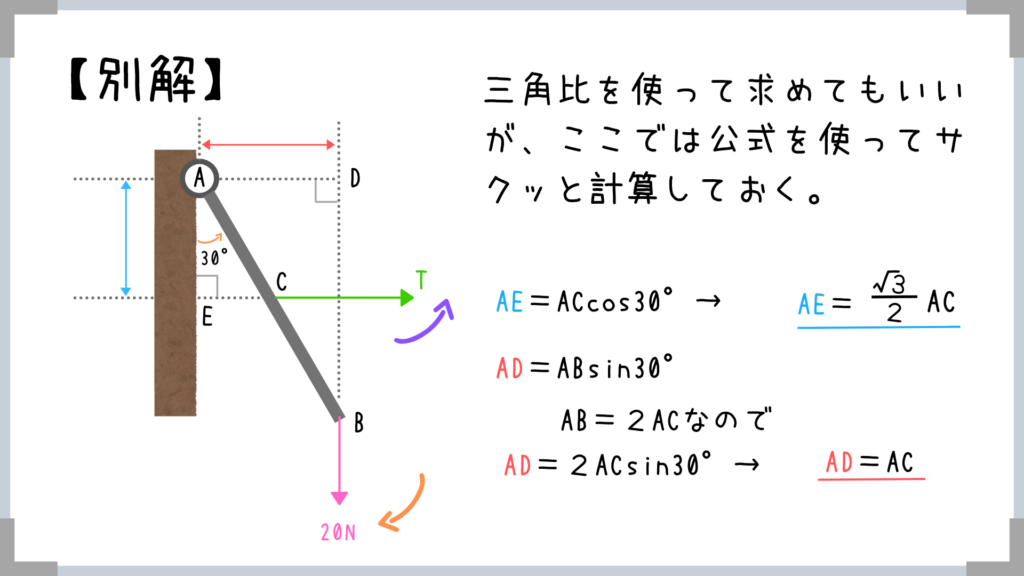
もちろん三角比を使ったほうが楽なら、三角比でOKです。
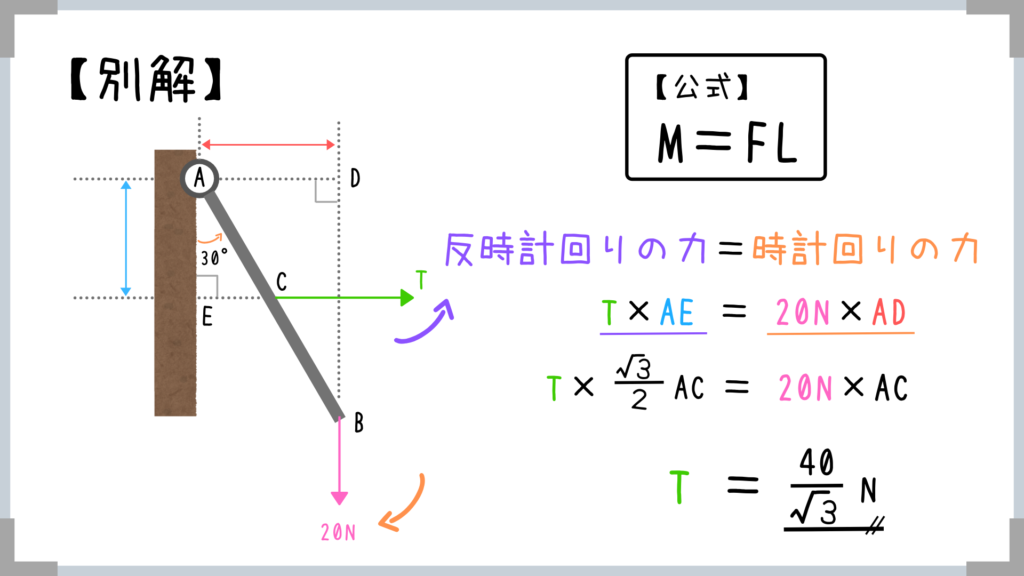
実はACにcosをかけるかTにcosをかけるか、ABにsinをかけるか20Nにsinをかけるかの違いだけなんですけどね。
まぁ難しい話は今はやめておきます。

公務員試験の問題も落とさないように他の分野も勉強していきましょう![
- 今ココ→①力のつり合い
- ②物体の運動
- ③エネルギーと運動量
- ④周期的な運動と慣性力
- ⑤電気と磁気(オススメ)
- ⑥波動
- ⑦熱と原子、その他
![公務員のライト[試験情報データベース]](https://senseikoumuin.com/wp-content/uploads/2022/12/cropped-logo-color-2.png)
















今は公務員試験の受験生の皆さんに物理が基礎となってる構造力学や水理学、土質力学なんかを教えています。
このページは『物理初心者の文系の方』に向けて書いたものです!
本気で解説していくから頑張って勉強していってくださいね!
ではさっそく物理対策スタート(^o^)/