苦手な人=公式を丸暗記する人!
力学系の分野って苦手な方が多いんですよね~!
でも、それって多分基礎的な部分が理解できていないまま先に進もうとしちゃっているからだと思います!
→このページは初心者向けに画像付きでわかりやすく解説しています!
それに、物理だからと言って数学的な考え方で覚えるんじゃなくて
「言語情報としてインプットする」ことが大事だと思いますよ~!
例えば加速度の単位は[m/s2]で、
コレをそのまま覚えようとすると意味わかんないですけど
「1秒当たり□[m/s]ずつ速度が上(下)がっていく」って読むことが出来たら
理解しやすくないですか?
主には公務員試験の物理対策として、
中学~高校の物理の分野すべてを解説していきますが、
もちろん中学生高校生の方が見ても参考になると思います!
ではさっそく【物体の運動】分野の勉強をしていきましょう!
- ①力のつり合い
- 今ココ→②物体の運動
- ③エネルギーと運動量
- ④周期的な運動と慣性力
- ⑤電気と磁気(オススメ)
- ⑥波動
- ⑦熱と原子、その他

目次
【力学:物体の運動分野】初心者向けに5項目を解説!
中学~高校物理の中でも、苦手な方が多く、挫折ポイントになってしまいがちなのが
【力学:物体の運動】分野だと思います。
この5つのテーマについて、基礎的な部分がわかるよう図でわかりやすく解説していきますね!
実はこの分野の問題って『考え方』『見方』を変えるだけで超簡単に見えちゃうんですよね~!
まぁごちゃごちゃ言っても仕方ないので、本編にまいりましょう!
【等加速度直線運動(速度と加速度)】単位に着目してみよう!
まずは「速度」と「加速度」について紹介していきます!
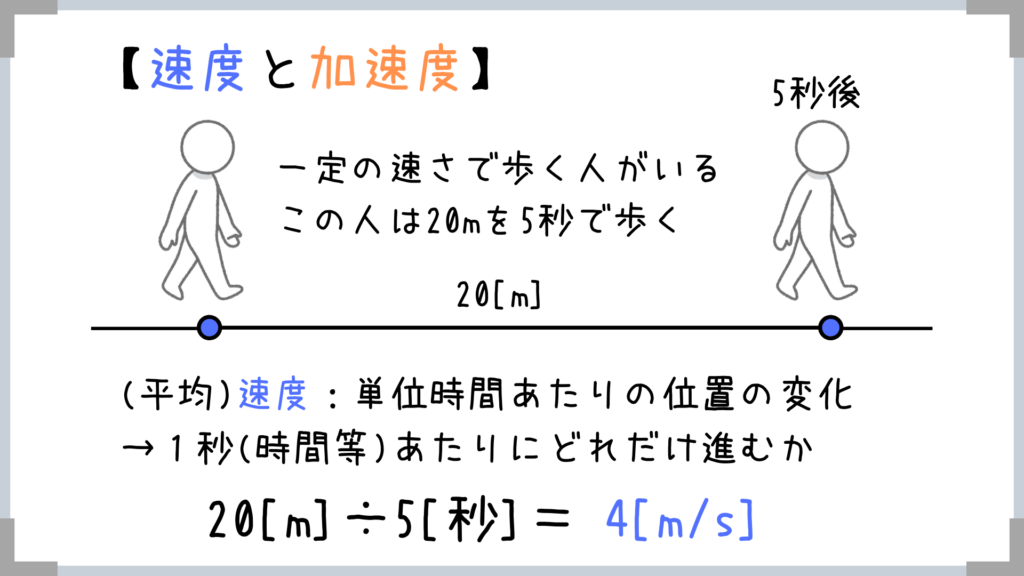
細かく言うとちょっと違うんですけど、一般的には↑のように覚えておけばOKです!
(単位[m/s]の分母[/s]は「1秒あたり」という意味です!)
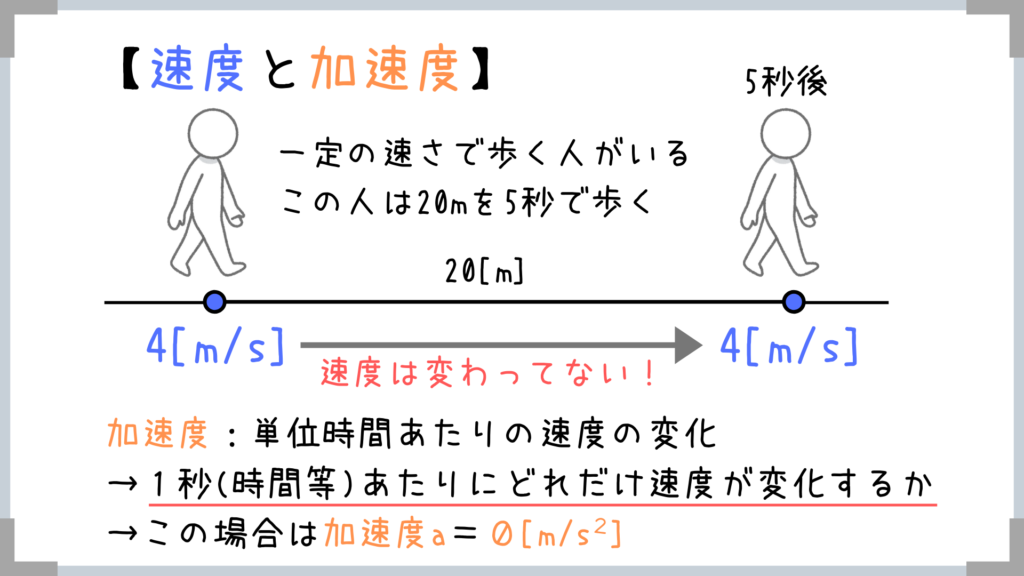
そしてこの例は「加速」してないですよね?
→ということは加速度はゼロ!
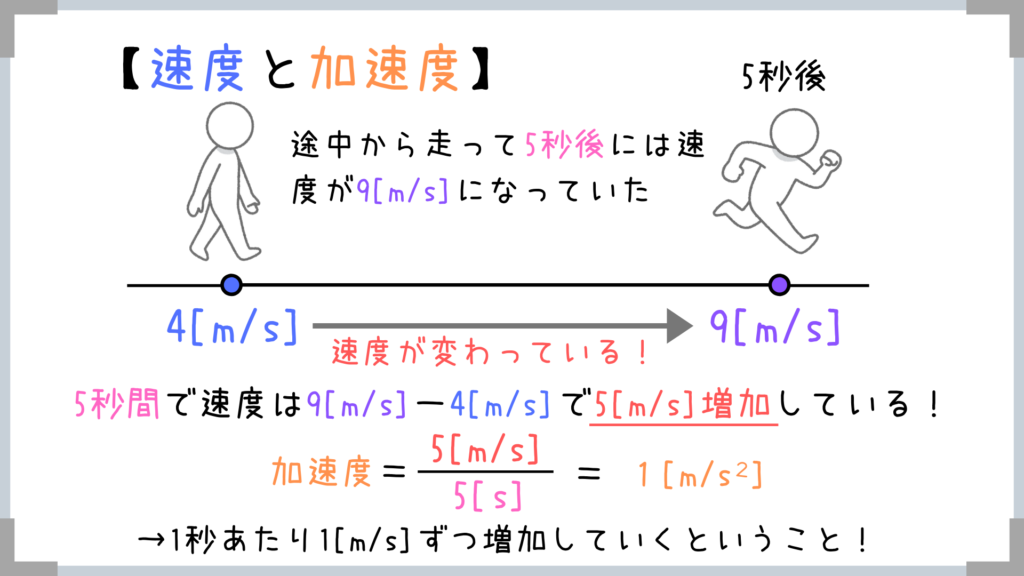
↑このように途中で速度が変わっているものには加速度があります。
単位に着目すれば意味が分かりやすいと思います。
分子が「速度」の変化量で分母が「時間」の変化量ですね!
→翻訳すると、「1秒あたりにどれだけ速度が増えるか」ということです!

この基礎部分を踏まえたうえで、この分野の勉強を行っていくと理解しやすくなると思います!
【等加速度直線運動の公式】文字の意味を把握することが大事!

覚える超重要な公式はこの2つ!
(もう1つありますが、↑の2つからtを消しただけなので無理に覚える必要はない)
…覚えらんないよ!!
って話ですよね!
でも実は文字の意味に着目してみると全然難しい公式じゃないんですね!
先ほどの棒人間の歩いている例をもう一回見てみましょう!
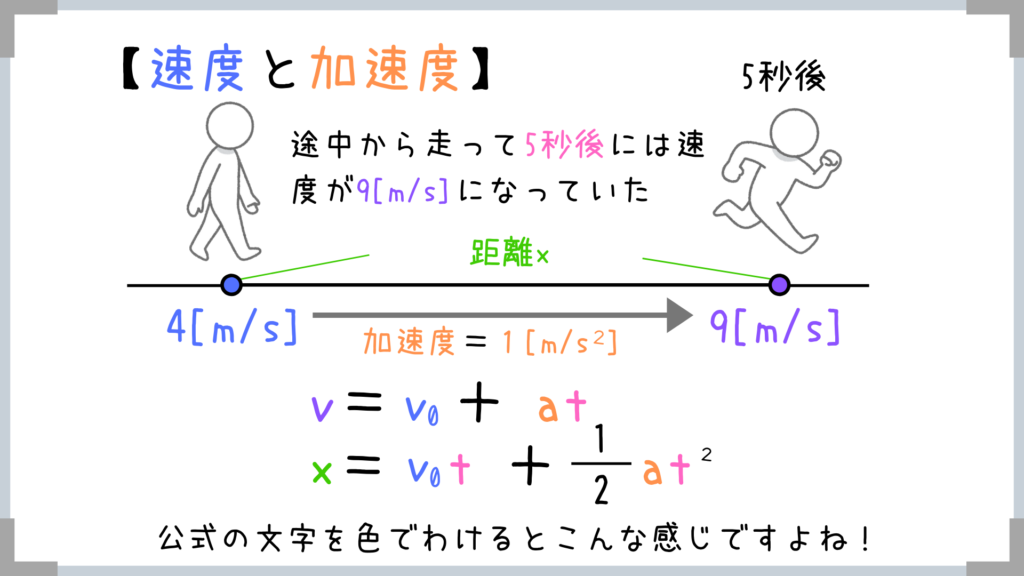
次にこの公式の文字の意味を言葉であらわしてみます。

1秒当たり1m/sずつ加速する
→5秒たったら5m/s増えている!
→4m/s(初速度)+5m/s(増えた分)
→9m/s!
文字の意味に着目すると覚えやすいでしょ~?
残念ながらもう1つの公式は直接覚えた方が早いと思います。
(実は速度を0-tの範囲で積分すると公式が導けますが覚える必要はないです。)
v=dx/dt=vo+at
→dx=(vo+at)dt
→x=vot+at2/2
速度を積分すれば距離(変位)の式が出せるんだ~って頭の片隅に入れておいて欲しいなと思います。
(式を忘れてしまった時用に)
ちなみに、今回紹介した例の距離[m]を公式を使って求めると32.5[m]ですね!

(1/2はわすれずに)
【等加速度直線運動の演習問題】裏ワザあり?
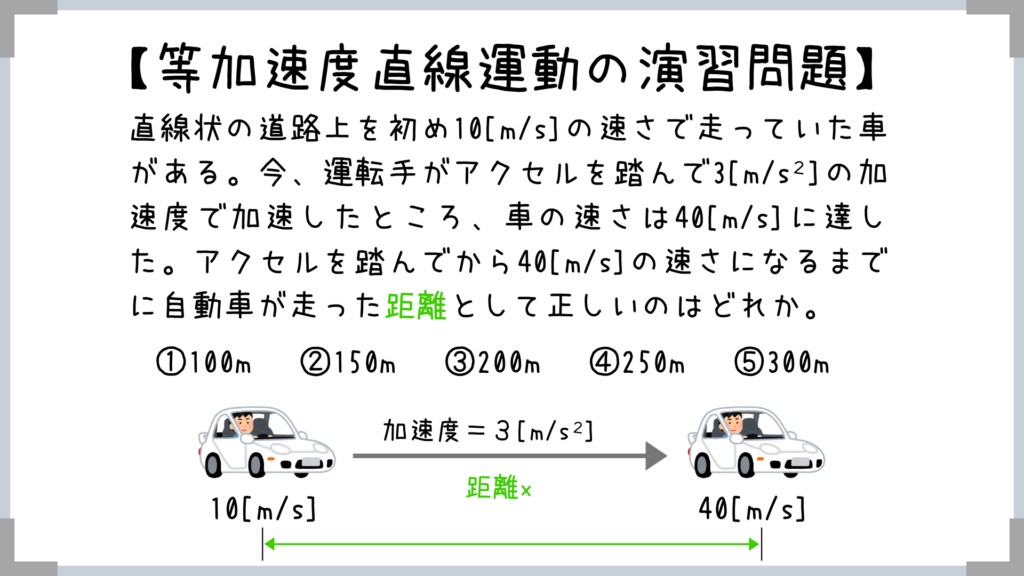
コレは公務員試験のいろんな過去問にも記載されているメジャーな問題ですね!
- まず「公式」を書く!
- わからない文字を1つ1つ丁寧に求めていく!
ここまでの話をきちんと理解してくださった皆さんなら余裕だと思います!


公式を使うだけなので、問題自体は簡単ですが、慣れるまでには時間がかかりますよね!
本番用に試験のコツみたいなものを紹介しようと思います。
もし公式を忘れちゃった場合、5択だからって適当にマークするのはNGですよ~!
例えばこの問題なら、1秒あたり3m/sずつ速度が増えていくわけですよね!
ということは
1秒後は13m/s
2秒後は16m/s…って強引に時間を求めることも出来ますよね?
10秒後が40m/sとなります。
この情報がわかるだけでも選択肢を切れますよね!
初速度が10m/sで、そこから加速してくって言ってるのに
選択肢①の100mは選べないですよね!
初速度(10m/s)のまま10sで100m進んじゃいますから。
それで残りの選択肢についてですが、
10m/s→40m/sになるってことは
平均すると25m/sってことですよね。
→10秒進むってことはだいたい250mくらいかな…
もし公式を忘れてしまったとしても
こうやってある程度選択肢を絞ろうと努力することも大事だと思います。
【自由落下】重要なのは考え方!初速度ゼロ、加速度=重力加速度!
先ほど紹介した等加速度直線運動の重要な2つの公式を思い出してください!
実はこの2つの公式に「a=g」、「v0=0」を代入するだけ!
※下向きを正とします。
- 下向きの加速度=重力加速度
- t=0で初速度はゼロ
まぁ実際にイメージすることが大切なので、さっそくこの式の意味を紹介していこうと思います。
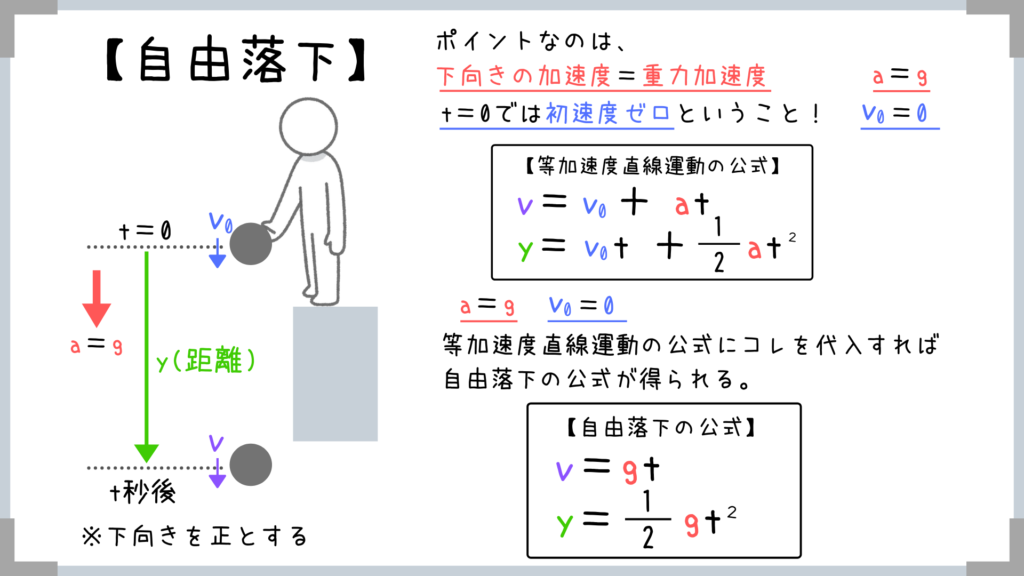
下向きに投げるなら初速度は発生しますが、手を離しただけでは速度を持っていません。
(離した瞬間って速度が無いですよね?)
また、下向きなので距離はyとしていますが、コレは意味がわかれば良いのでxと置いたままでも「距離=」と自分がわかるように書いても別にOKです!
(基本的にはタテ軸をy、ヨコ軸をxとします)
まぁ等加速度直線運動の公式の使い方が分かっていれば自由落下の式が導けるので、「自由落下の公式」として特別に覚える必要はありません!
その代わり等加速度直線運動の公式と自由落下の考え方はマスターするようにしましょう!

それを等加速度直線運動の加速度の部分に代入すればOKです!
実際にその状況をイメージしてみることが大事!
【鉛直投げ上げ】公式は覚えなくていい!考え方を覚えよう!
先ほど紹介した等加速度直線運動の重要な2つの公式を思い出してください!
実はこの2つの公式に「a=ーg」を代入するだけ!
※上向きを正とします。
上向きを正としているので重力加速度は下向き(マイナス方向)にはたらく
→球を減速させようとする!
実際に球を上に投げると球はどんどん減速していくでしょ~?
そして、先ほどの「自由落下」の場合は初速度がゼロだと言いましたが、
「鉛直投げ上げ」の場合、初速度は確実にゼロではないですよね!
→初速度が無いと上に投げられませんからね(汗)
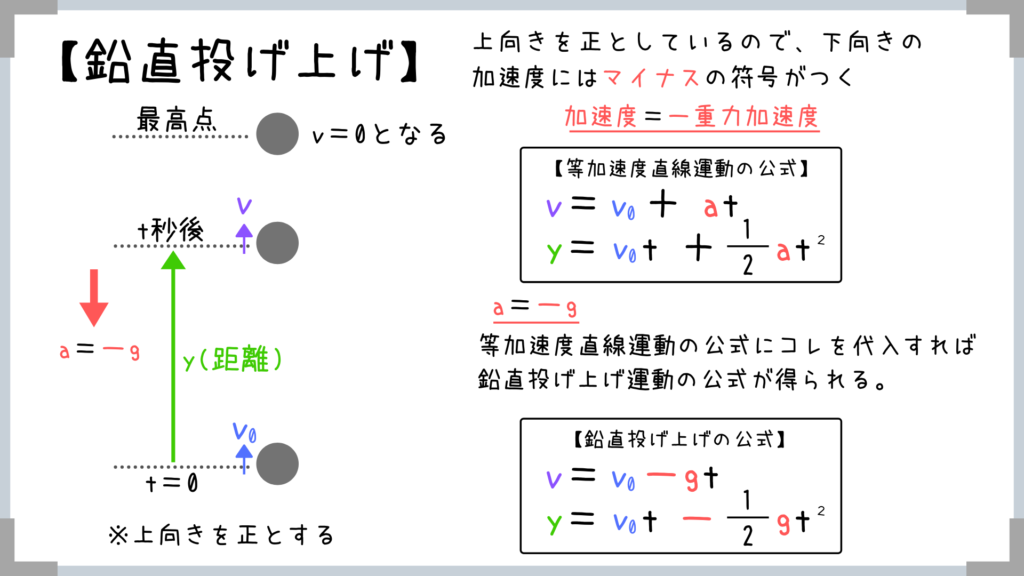
鉛直投げ上げの公式も、自由落下と同様に公式をそのまま覚える必要はありません。
鉛直投げ上げの考え方と等加速度直線運動の公式の使い方をマスターしておけばOKですからね!
そして鉛直投げ上げ運動でもう1つポイントなのがコレ!
- v=0になる時がyの最大値!
→ボールを上に投げた時に一番高く上がったところでは速度がゼロになるでしょ? - v=0となる地点までの時間を求めることが出来れば、最高地点までの距離も求められる!
↑このポイントが問いとなっている問題って
高校の物理の試験でもきっと良く出るんじゃないかなと思います。
公務員試験でもたまに出題されているので、早速問題を1問解いていきましょうか!
【鉛直投げ上げの演習問題】解法手順は決まっている!
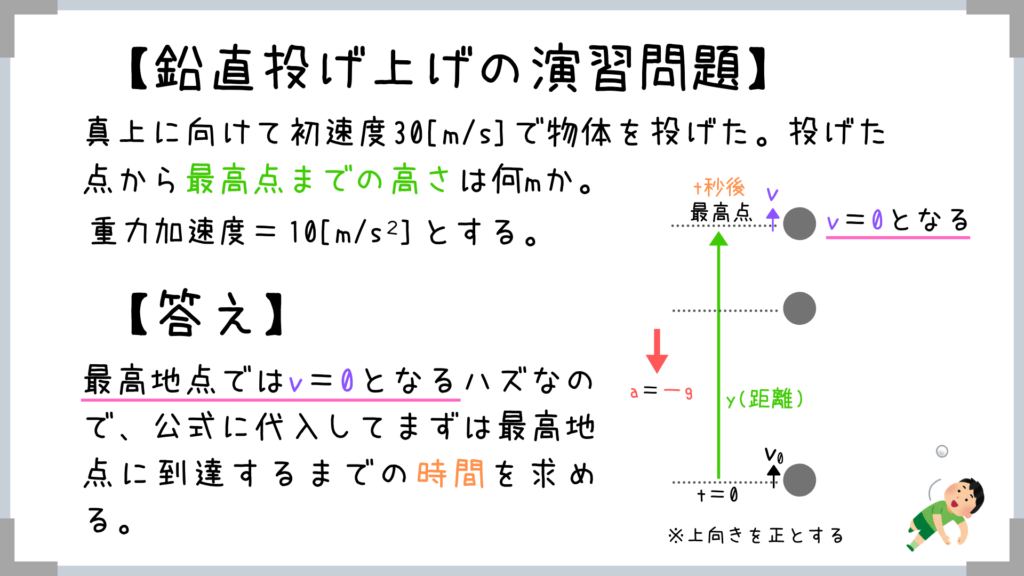
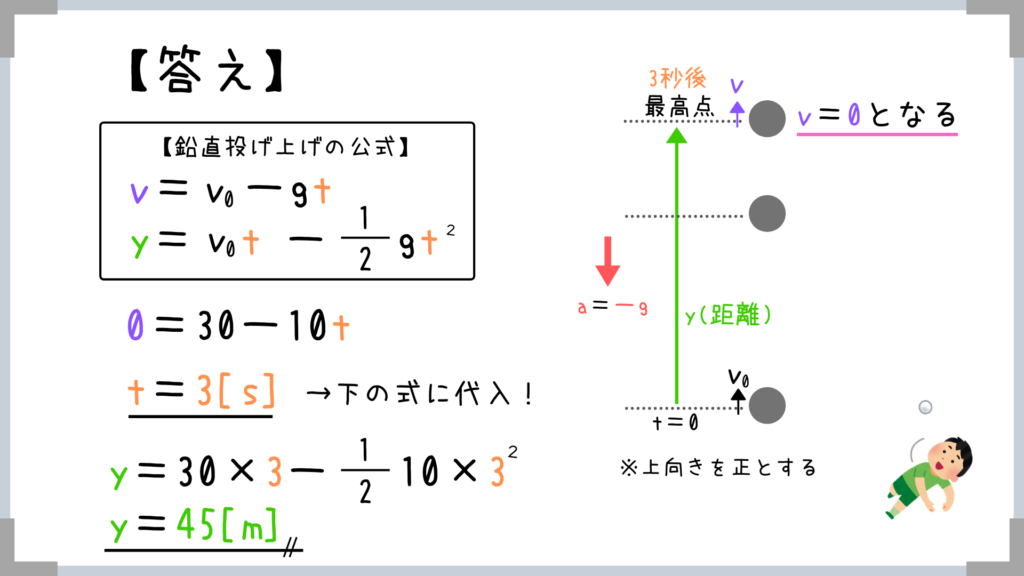
先ほど紹介した「最高点でv=0となる」というポイントをおさえていれば簡単な問題ですよね!
まずは最高地点に到達するまでの時間を上の公式で求めて、時間が求まったら下の公式で距離を求めれば終わりです!
なんとなく鉛直投げ上げの考え方と公式の使い方がわかりましたか?
等加速度直線運動、自由落下、鉛直投げ上げの基礎が理解できたところで、次はこれらの知識の集大成、「放物運動」について紹介していきたいと思います!

最近では平成27年の特別区で出て、同じような問題が翌年地方上級で出題されていました。
【放物運動】速度をタテとヨコに力を分解して考えるだけ!
物理の問題で出題される放物運動は「水平投射」と「斜方投射」の2パターンあります!
どちらもおさえるポイントは同じ!
- 速度をタテとヨコに分解して考える
→それぞれの速度を別物だと思って考えるのが大事! - 横向きの力は加速度ナシ!
→横向きの速度は初速度(一定)でずっと移動する
ちょっとイメージしにくいと思いますので、「水平投射」と「斜方投射」それぞれ図で公式を紹介していきたいと思います。

速度をタテとヨコに力を分解して考えるだけなので楽勝楽勝(^^)/
【水平投射】横向きの速度は初速度で一定!
水平投射というのは↓こんなものですね!
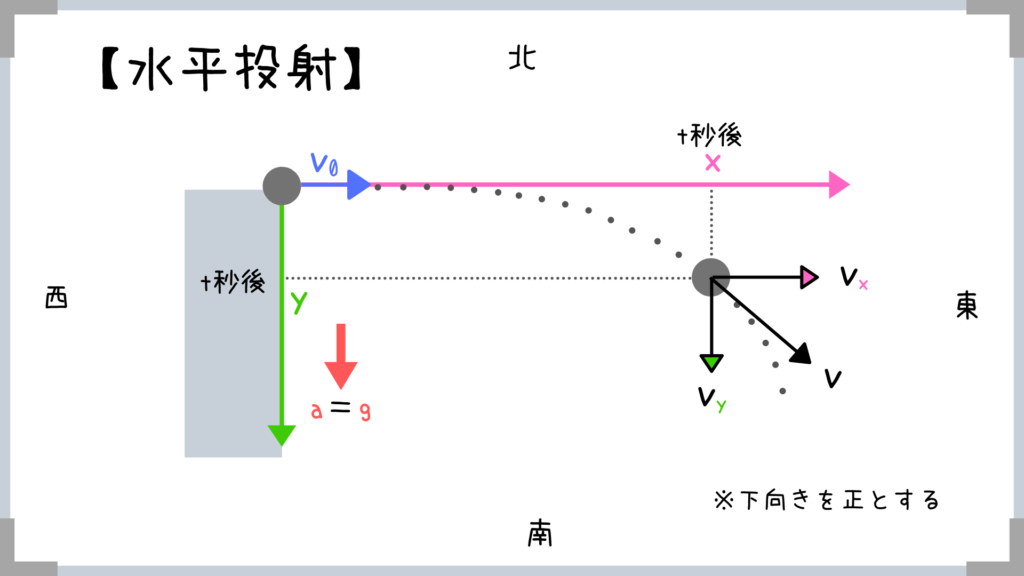
t秒後の球の速度と距離の関係も式であらわすことができるんですね!
でも、コレを直接覚えるのってナンセンスだと思うんですよね~!
ということでコイツをタテとヨコでそれぞれ別に見ていきましょう!
ヨコはヨコだけの速度・距離をタテはタテだけの速度・距離を考えていきます!
単純に片方を無視すればいいのですが、
情報が混雑してこんがらがってしまいがちなので、
まずは『北から南』を見てみましょう!
(タテの運動を無視!ヨコの運動のみに着目する)
ヨコの動きのみに着目!
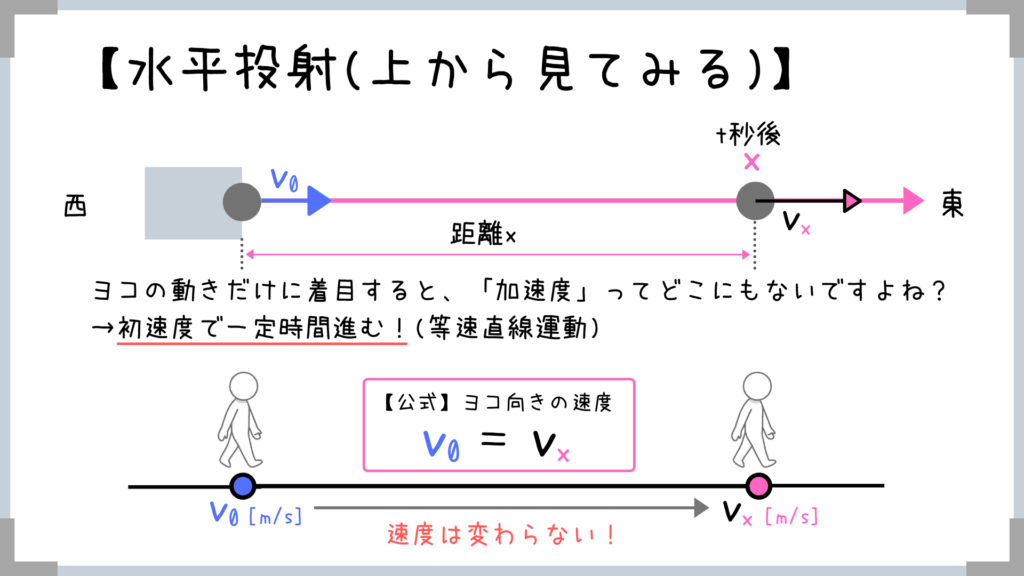
上から見ると考えやすいですよね!
横向きの速度は「初速度で一定」です!
→加速度はどこにもないですからね!
では次距離の公式!
ココまで理解出来たら距離なんてすぐ出せますよね!
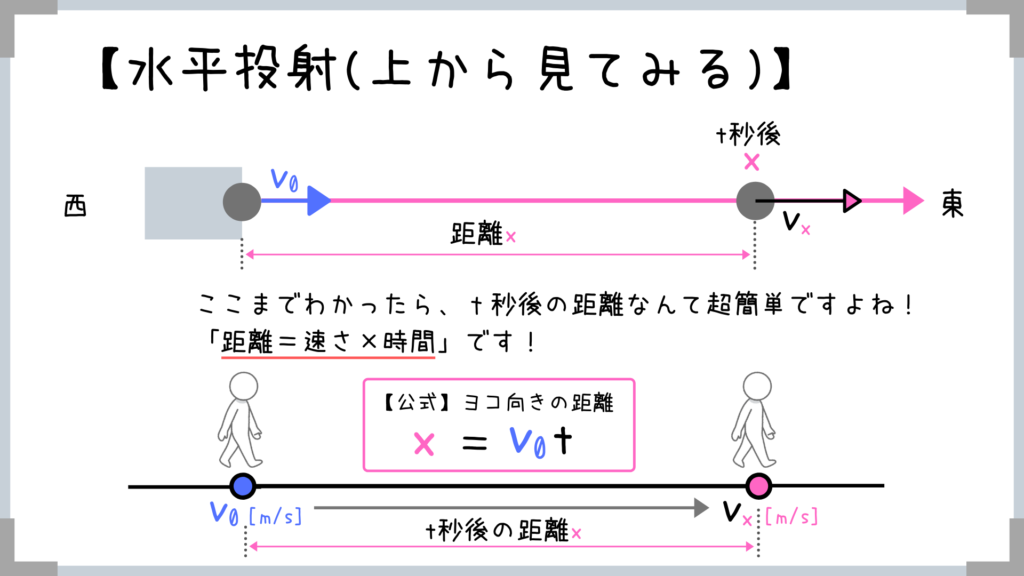 距離=速さ×時間なので
距離=速さ×時間なので
「x=v0t」が公式となります!
タテの動きのみに着目!
では次に東(ヨコ)から見てみましょう!
こっちはさらに簡単です。
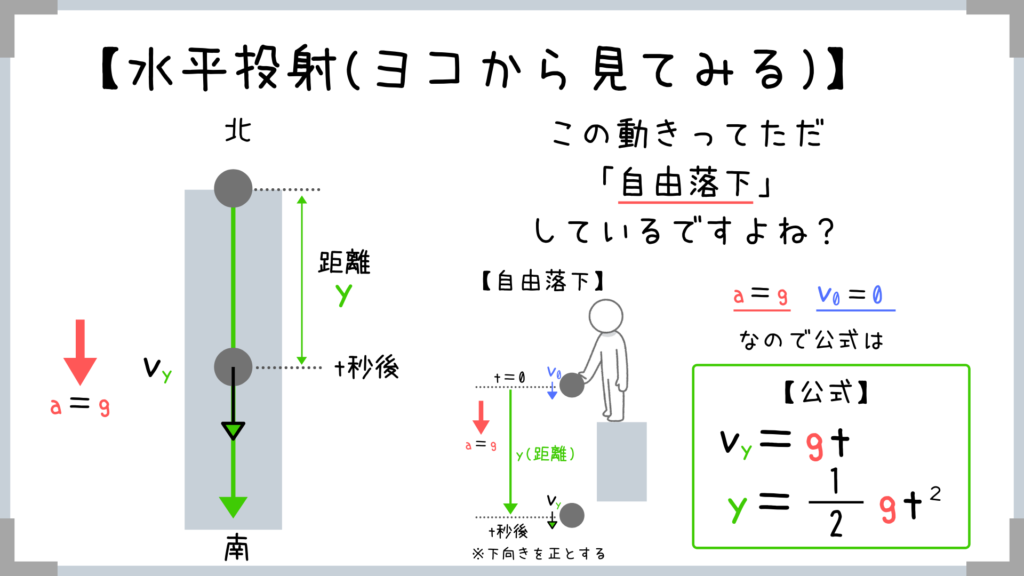
タテ方向の動きは「自由落下」しているだけということになります!
なので公式も「自由落下」と同じ!
【水平投射の公式まとめ】
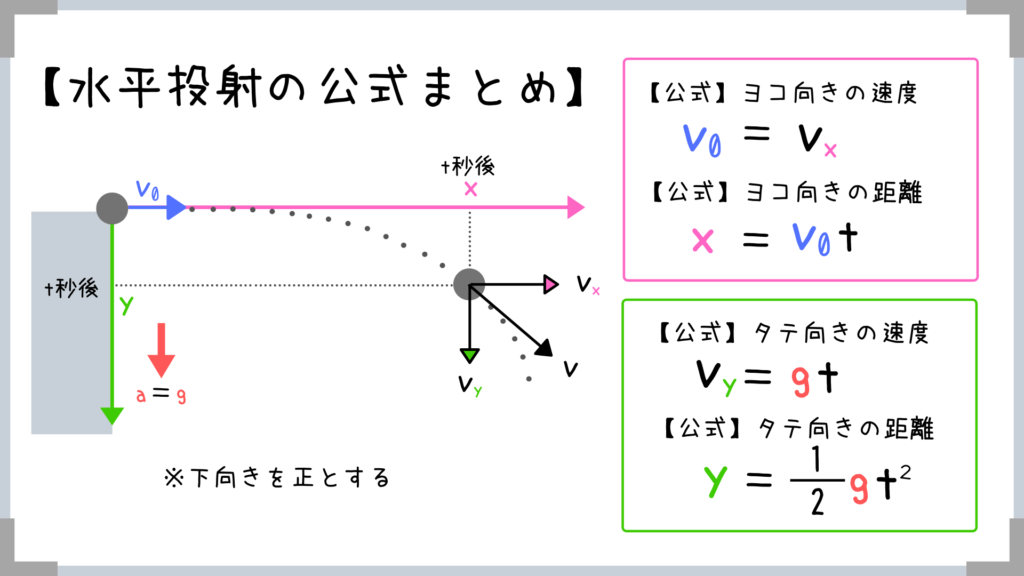
水平投射の公式をまとめるとこんな感じ!
要は「水平投射」というのは
横向きに「等速直線運動」
縦向きに「自由落下」をしているだけということです!

このように1つ1つ紐解いて考えていくと理解しやすくなります!
【斜方投射】よく出題される!
公務員試験でも「斜方投射」の問題はよく見かけますし、高校物理の試験でもきっと良く出るんじゃないでしょうか。
ポイントは先ほど紹介した「水平投射」と同じで、タテとヨコに成分を分解して考えること!
まず最初に「初速度」をタテとヨコに力を分解することが大切!
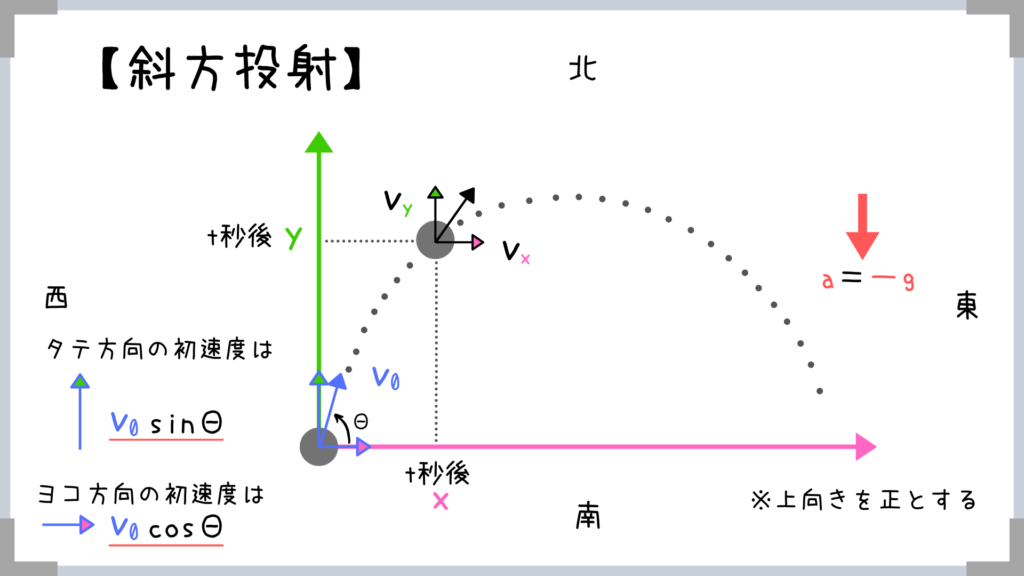
成分の分解方法が分からない人は以下のページをチラッと見てみて下さい!
→【力の分解方法】
初速度をタテとヨコに分解できたら、
あとは「水平投射」と同様で
球の動きもタテとヨコそれぞれ別に考えていくことが大事!
ヨコの動きのみに着目!
ヨコ方向の動き以外シャットアウトしたいので
まずは『北から南』を見てみましょう!
(タテの運動を無視!ヨコの運動のみに着目する)
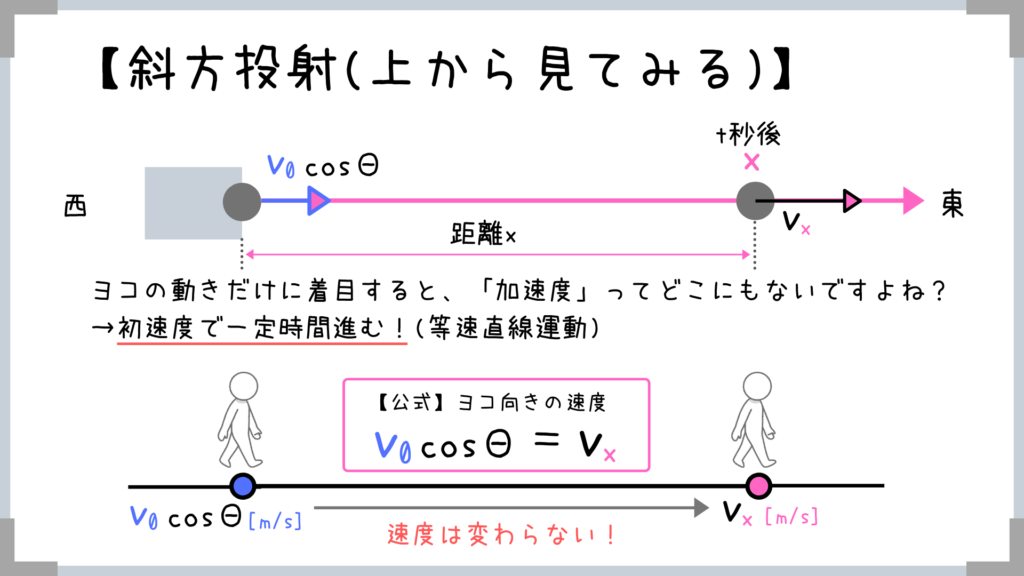
初速度が分解出来たら考え方自体は単純ですよね!
横向きの速度は「初速度で一定」です!
→加速度はどこにもないですからね!
では次距離の公式について紹介しますが、
単純に「距離=速さ×時間」なので解説もくそもありません!
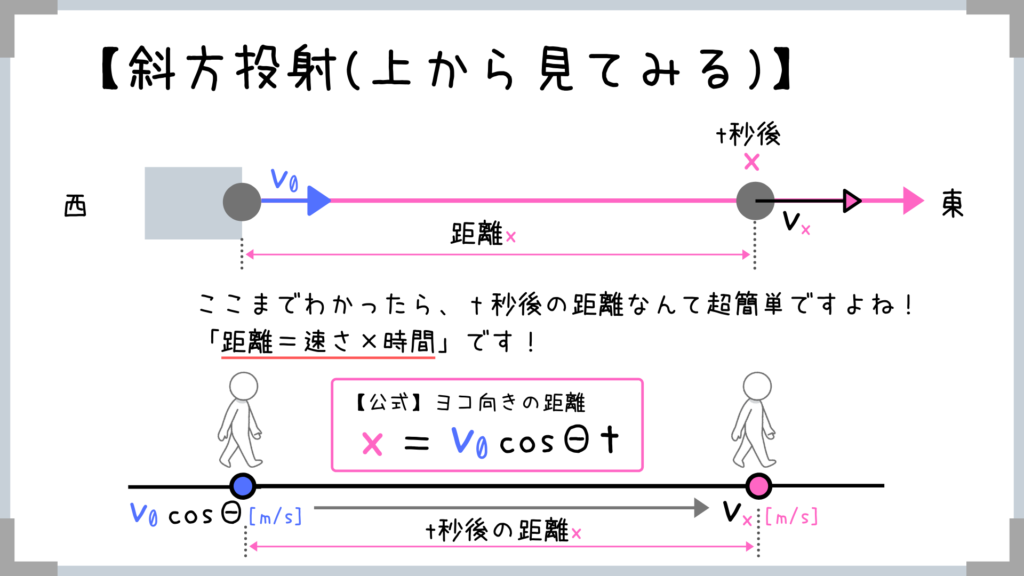
初速度がv0cosΘということにだけ注意すれば考え方自体は単純ですよね!
タテの動きのみに着目!
では次に東(ヨコ)から見てみましょう!
実はタテ方向の動きにだけ着目すると
「鉛直投げ上げ」運動をしているだけということになります!
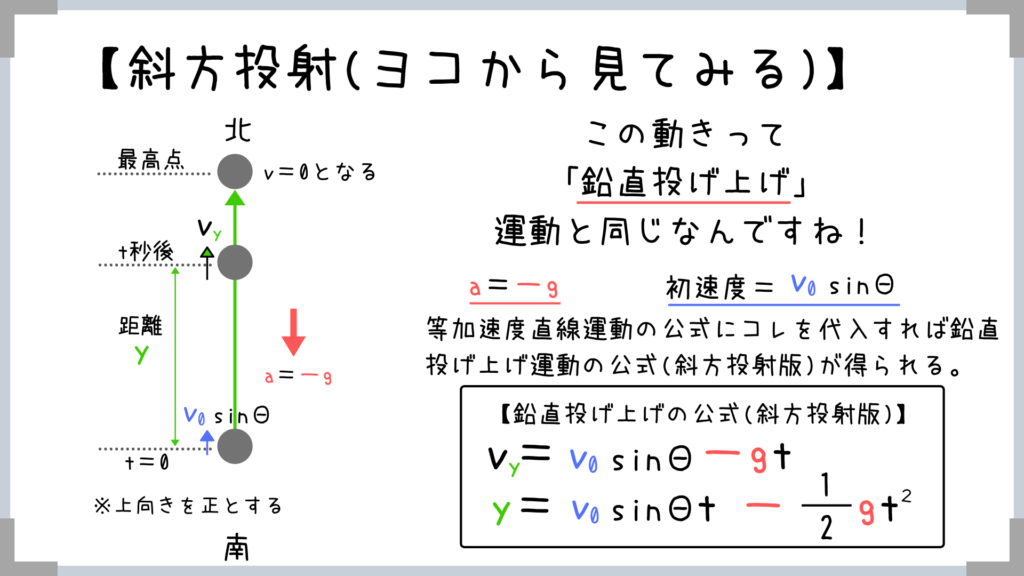
鉛直投げ上げ運動の公式を覚えておけば
初速度にsinΘがついただけということになります!
ちょっと文字がたくさん出てくるので、覚えるのが大変ですかね?
でも、公式を覚えるというより、考え方を覚えることの方が大事です。
公式がうんたらかんたらと言ってきましたが、 誘導付きの問題なので少しやさしめですが、大事なポイントがおさえられているので非常にいい問題だと思います。 まず、タテ方向の速度について考え、床に落ちるまでの時間を求めます。 鉛直方向の速度は最高点でゼロになるという考え方はよく使うので、知識として覚えておきたいですね! 鉛直投げ上げの上の公式にわかっている値を代入すれば そしてポイントなのが ヨコ向きの運動というのは、初速度一定で等速直線運動をしますから ちょっと難しく感じた方も多いかもしれません。 公務員試験に出ている問題って同じパターンの問題が多いですから、このような手順を覚えておくといいかもしれません。 あとは鉛直投げ上げの公式の距離の公式で「y=0」と代入して 物体にはたらく力と物体の運動との関係について、次の3つの法則が成り立ちます! なんの話だ…って感じですよね(汗) 物体に外部から力がはたらかないとき、または、はたらいていてもその合力が 0 であるとき、静止している物体は静止し続け、運動している物体はそのまま等速度運動(等速直線運動)を続ける。 う~ん。意味わからん…って話ですよね! よくあるのが「電車での急発進」の例です! 乗っている電車が発信するときに、進行方向と逆向きに倒れそうになることがあると思います。 個人的には「宇宙でだるま落とし」っていうのがイメージしやすいんじゃないかなと思います。 大きな天体が無ければ、重力も摩擦も空気抵抗もはたらかない 飛ばされたパーツは外部からの力がかからないため、一定の速度で真っ直ぐに進んでいくことになります! 地上でだるま落としをするとそのままの状態を保とうとはしますが、地球からの重力や摩擦力で上のパーツは下へ、飛ばされたパーツと触れ合っているパーツは摩擦力で少しずれますからね。 まぁ実際に問題が解ければいいだけなので、こんな感じなんだ~っていう程度で覚えておけばOKです。 運動の法則は大事です! 物体に力がはたらくとき、物体には力と同じ向きの加速度が生じる。その加速度aの大きさは、はたらいている力の大きさFに比例し、物体の質量mに反比例する。 1[kg]の物体に1[m/s2]の加速度を与える力を1[N]と定義したのがニュートンというわけですね! まぁそんなことは置いておいて 符号の設定ミスで間違いを導いてしまうこともあるので、どちらが「正」の向きかという点は意識した方がいいと思います。 では、これらのポイントをおさえて実際に解いていきます! 解法の手順は以下の通りです。 かなり図を丁寧にかきましたが、物理という科目は図を丁寧にかくのがめちゃくちゃ大事です! あとはこの加速度、その他の数値を等加速度直線運動の公式に当てはめるだけです! 「物体Aが物体Bに力を加える(作用)とき、物体Aは反対向きで同じ大きさで同一作用線上にある力を物体Bから受ける(反作用)」ことを作用反作用の法則といいます。 作用反作用の法則の条件は以下の通りです。 作用反作用の2力は まぁコレだけ聞いてもパッとしませんよね! 具体的な例を挙げるとこんな感じです。 簡単に言うと、押す力がはたらいたら、その物体からも押し返す力がはたらいているよということです。 この『作用反作用』と呼ばれるもの、 もう少しイメージしやすくするためにももう1つ例を挙げて紹介していきたいと思います。 同じ色の矢印同士が作用反作用の関係にあります! 力のつり合いは1つの物体に働く力の関係 なんとなく違いがわかりましたか~? また、mg=T=X=Y=Zとすべての力が等しいですよね! まぁぐちぐち言っても仕方ないので、 ニュートンの運動の法則のフルコース問題がこちら。 先ほども紹介しましたが、重要なのでもう一度ポイントから紹介! そして、先ほど作用反作用の法則のところでも話しましたが、 これらのポイントをふまえて問題を解いていきましょう! 解法の流れは先ほど紹介した運動の法則の演習問題と同じですが、求めるものが加速度なので④は省略! 作用線と並行の力への分解をmgsin30°で求めちゃってますが、 また、物体Aにはたらく張力Tと物体Bにはたらく張力Tは等しいということもポイントの1つですよね! このように物体がいくつ出てきても 変な見方をすれば、左向きに「F=ma」という力を加えることによって、物体を静止させている状態とみなすことができちゃうということになりますよね。 最後に作用反作用の法則の頻出項目について簡単に解説して 物体が重なっている時や触れ合っている時は もう1つばねの問題も良く出るので、考え方の解説だけしておきますね! はい、これで【力学:物体の運動分野】の解説終わりです! 何となくイメージ掴めましたか? この分野はちょっと難しいと思いますので ながながとお疲れ様でした! 
では、斜方投射の過去問を1問解いていきましょうか!【斜方投射の演習問題】結局は過去問が解ければOK!
結局過去問が解ければそれでOKですから
実際に公務員試験(地方上級)で出題された問題を1問解いていきましょう!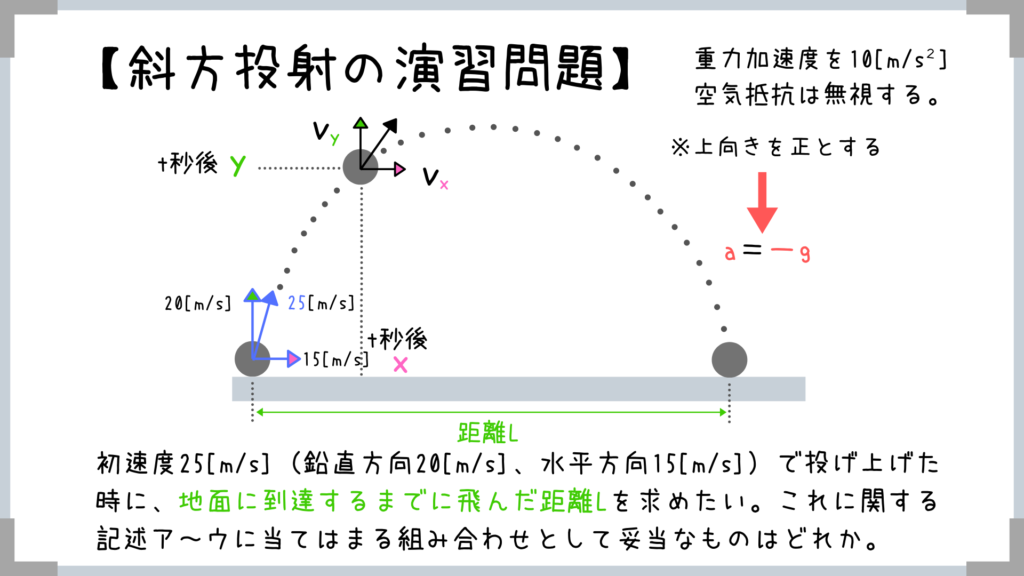

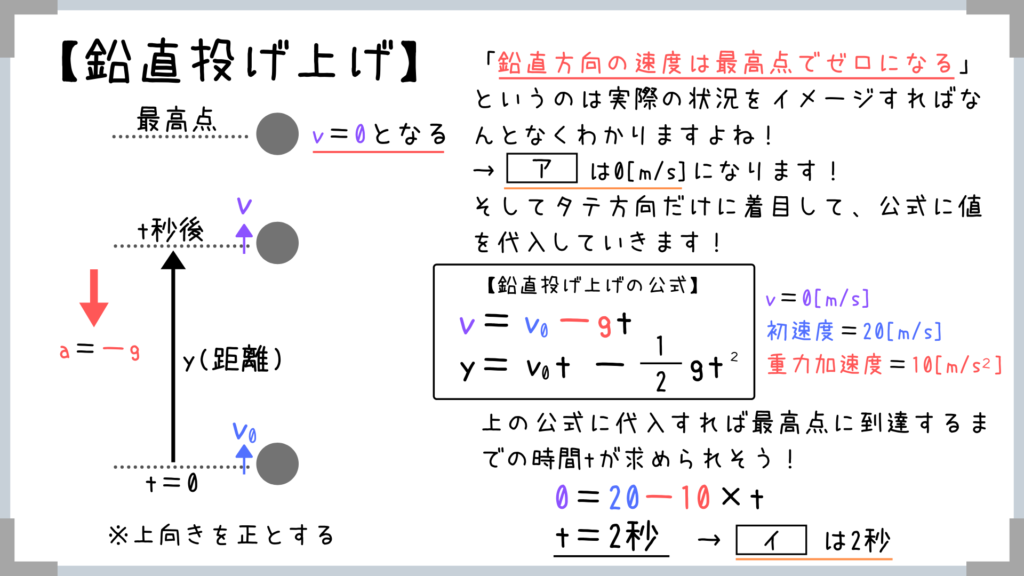
「最高点に到達するまでの時間」を求めることが出来ます!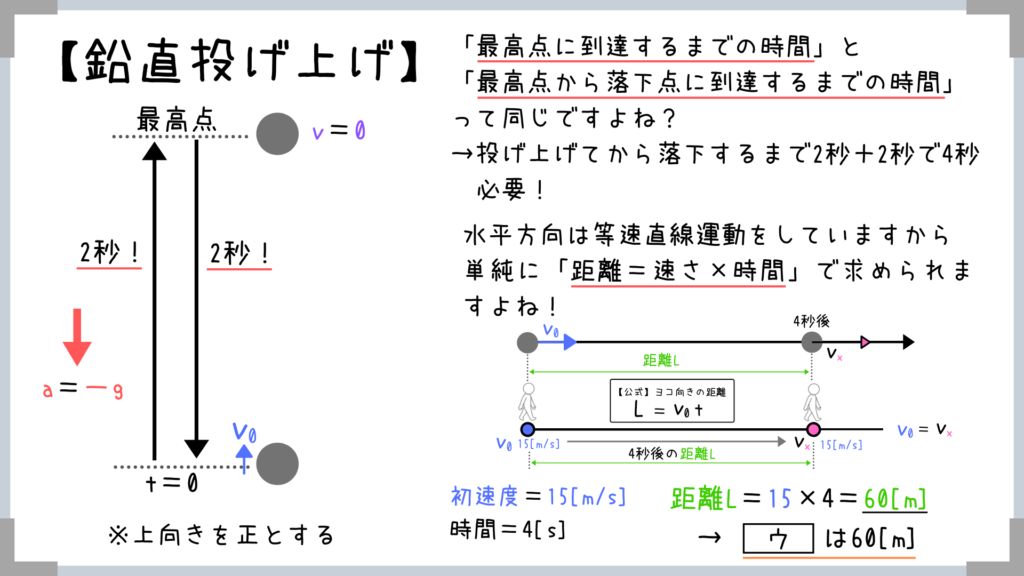
『投げ上げてから最高点に到達するまでの時間』と『最高点から落下点に到達するまでの時間』は等しいということです!
この問題でいうと
最高点までに2秒かかって、そこから地面に落下するまでの時間も2秒かかるということですね!
→投げ上げてから落下するまで4秒を要するわけです。
この時間を利用すれば、ヨコ方向に移動した距離なんて超簡単に求められちゃいますよね!
でも実は、解法手順って決まっているんですよね!

アが0m/sと分かった時点で選択肢は①~③のどれか、
イが2秒と分かった時点で…
①が答えだとわかっちゃいますよね!
公務員試験は時間との勝負という部分もありますから、選択肢を見る癖はつけていきたいですよね!
投げ上げてから落下するまでの時間を求めてもOKです!
→投げ上げる位置と落下地点ってタテ方向でみるとゼロですよね!
0=20×t – 10×t2/2
→t=4[s]
【ニュートンの運動の法則】難しい話じゃない!
でも実際にイメージするとそんなに難しいことを言っているわけではないので、サクッと紹介していきますね!運動の第1法則『慣性の法則』とは?
これは、電車が進行方向の向きに運動しようとするのに対し、人は静止し続けようとするため、人に進行方向と逆向きに見かけの力がはたらくからなんですね!
このような「慣性」によってはたらくみかけの力を慣性力と言います!
(→覚える必要はありませんが、慣性力の大きさはF=-maとあらわせます)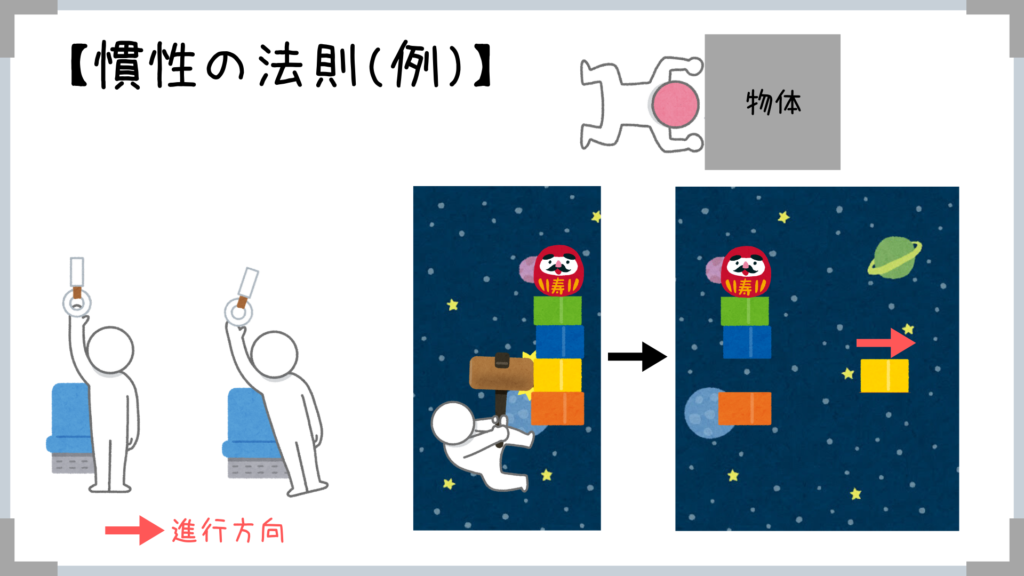
→外部から加わる力がないため、物体は完全に慣性の法則に従う!
そして、飛ばされたパーツ以外のパーツもそのままの状態で静止すると思います。
→このような性質を「慣性」というわけですね!
→この時上のだるまが一瞬その場にとどまろうとしますが、コレも慣性の法則によるものです。運動の第2法則『運動の法則』とは?
問題としてもよく出題されている方だと思います。
式で表すと『ma=F』とあらわせる。
「質量×加速度=力」←この式を『運動方程式』という。
これを記念して[kg・m/s2]という単位が[N]となりました!
実際の問題を1問解いていきましょう!【運動の法則の演習問題】試験で出る問題は単純なものばかり!

(わからない時は正になりそうな方を正と仮定しておけばOK)
また、「滑らかに」という記載がある場合、「摩擦力を無視」するるのですが、コレは物理の世界では良く出てくる表現なので、絶対に覚えておきましょう!
(→実際はあり得ないんですけど、氷の上よりツルッツルということですね!)
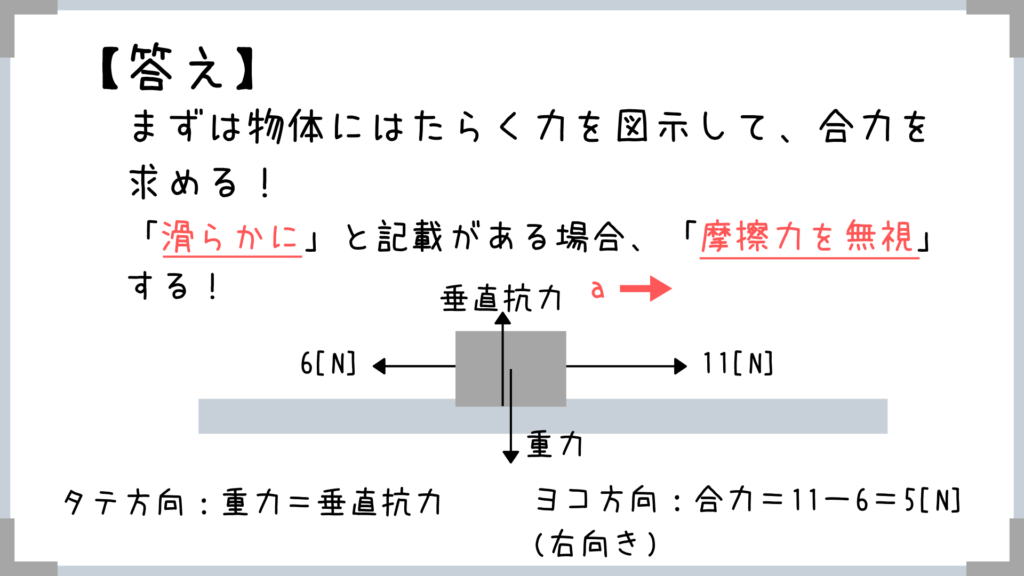 今回はあからさまに右向きに運動するなってわかるので、右向きを正と仮定して加速度の矢印を描きましたが、この向きは仮で適当においても大丈夫です!
今回はあからさまに右向きに運動するなってわかるので、右向きを正と仮定して加速度の矢印を描きましたが、この向きは仮で適当においても大丈夫です!
とりあえず自分がこっちが正になりそうだなって方に矢印を向けておきましょう!
→仮に左向きに置いたとしたら、マイナスがつくだけなので、計算自体に支障はでない!
(まぁ少しはめんどくさくなるかもしれませんが(汗))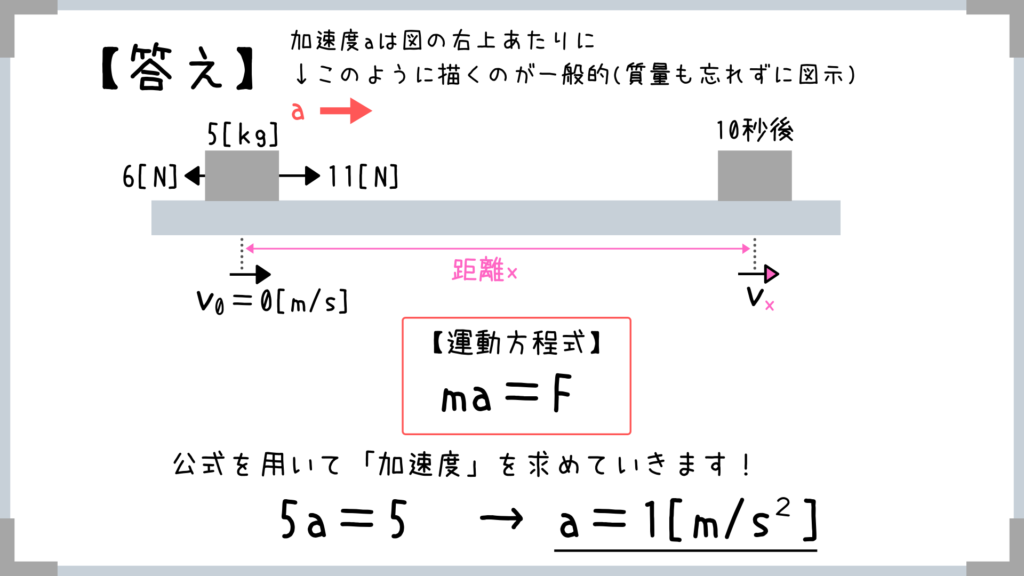
運動方程式を用いれば、加速度は1[m/s2]とラクに求めることができますよね!
(→1秒当たり1[m/s]ずつ加速していくということですね)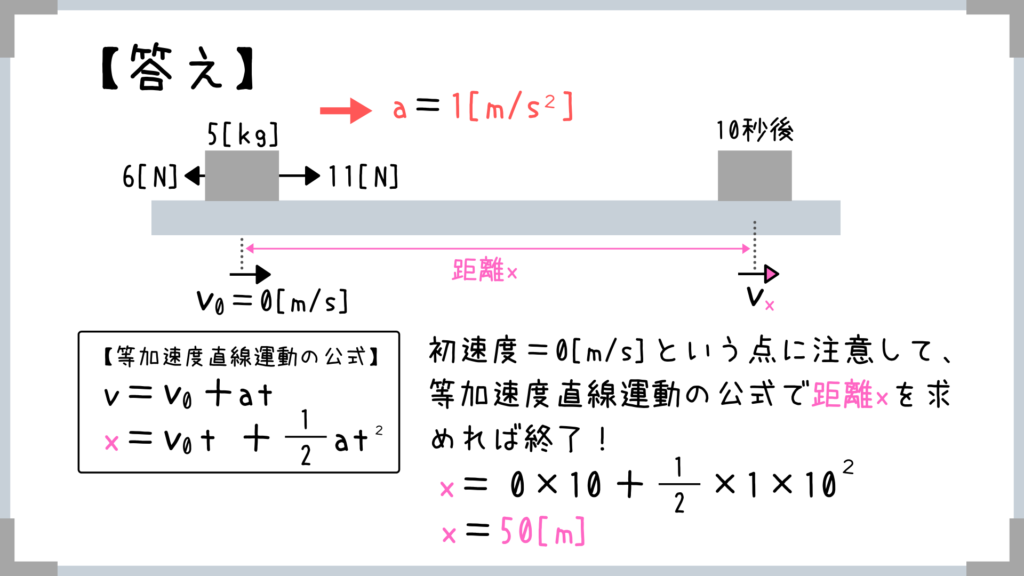
t=0の時点では速度を持っていないという点にだけ注意が必要ですね!
あと、慣れるまでは「等加速度直線運動」を使うかもって思ったら「とりあえず2つの重要な公式を書く」という癖をつけることも大切だと思います!
次の「作用反作用の法則」のところでも運動の法則を使う演習問題をやるので、もう1問やってこの分野の問題はマスターしちゃいましょう!運動の第3法則『作用反作用の法則』とは?
①同一線上にある
②力の大きさが等しい
③互いに反対向き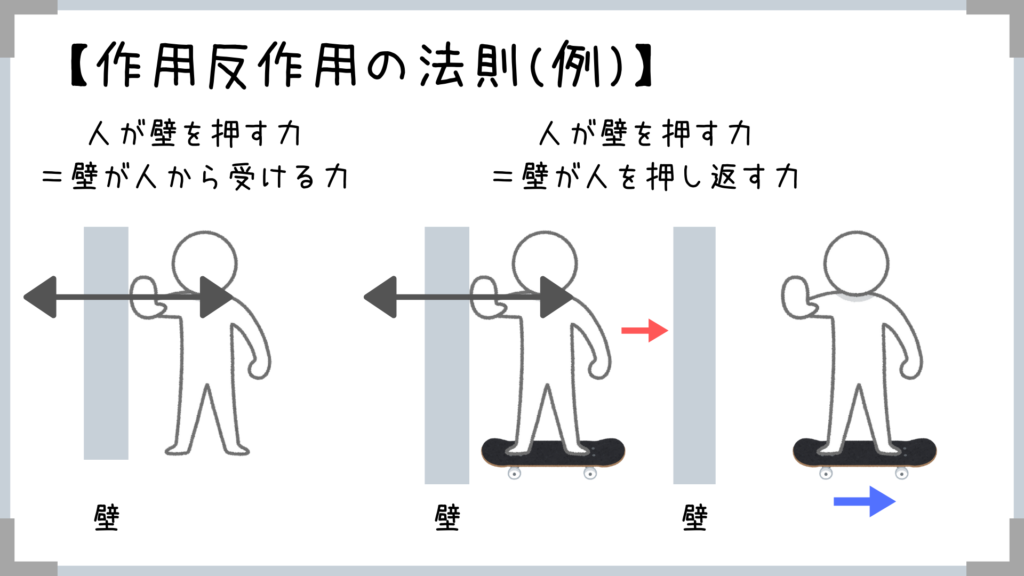
実は「力のつりあい」とは違うんですね~!
もうこんがらがっちゃいますよね(汗)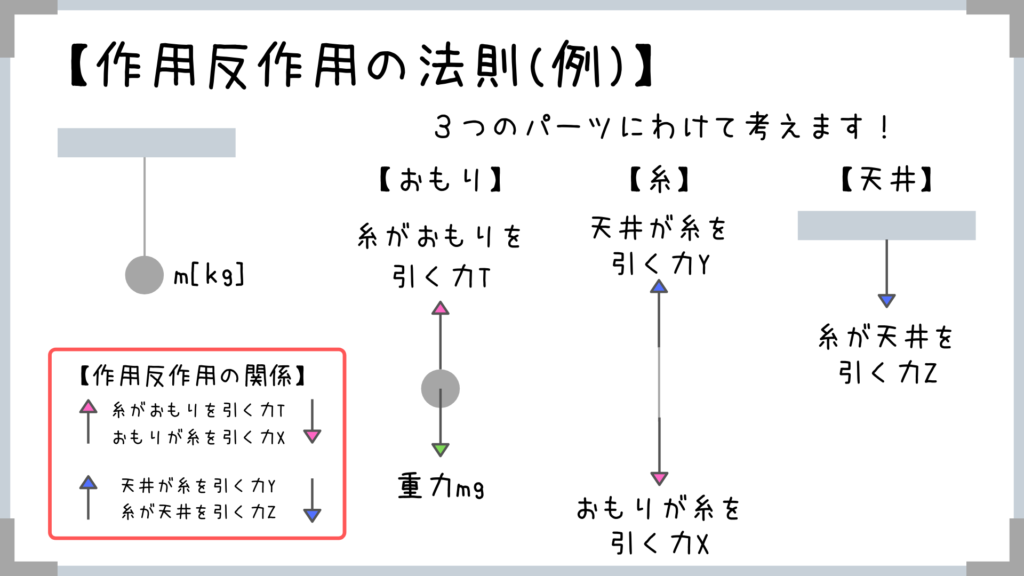
そして、「力のつり合い関係」にあるのは、「T=mg」と「X=Y」です!
作用反作用は2つの物体の間でお互いに働く力の関係
ここら辺の考え方も大事になってきます。
→球から天井までは一直線なのに、糸を伝って天井を引っ張っている力の大きさと自分が引っ張っている力の大きさが違ったらおかしいですよね?
さっそく演習問題を解いていきましょうか!【ニュートンの運動の法則の演習問題】フルコース!
過去の公務員試験(地方上級)で出題されている良問(改題)ですね!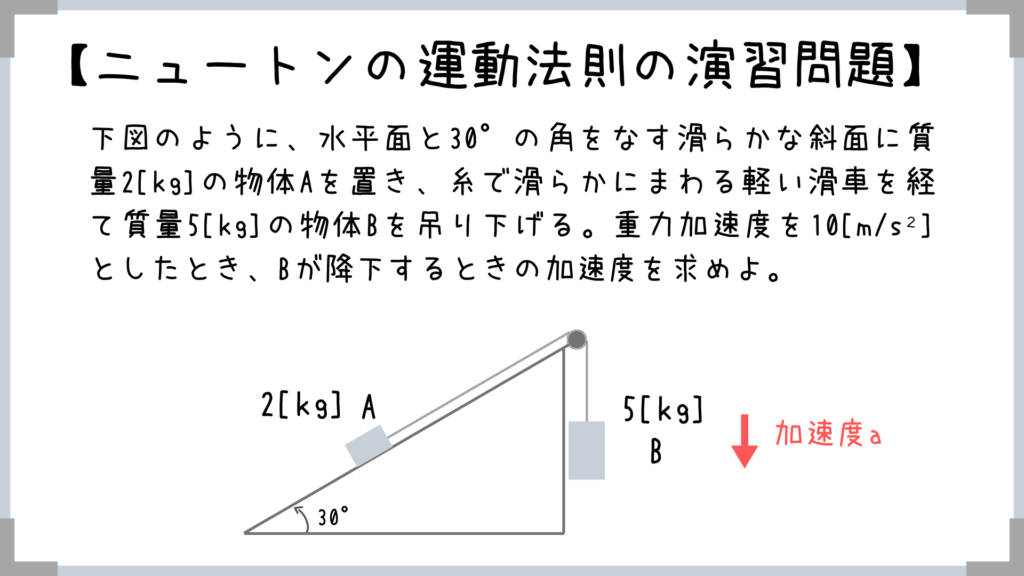
(わからない時は正になりそうな方を正と仮定しておけばOK)
糸が物体Aを引く力と物体Aが糸を引く力、
糸が物体Bを引く力と物体Bが糸を引く力は等しいですよね!
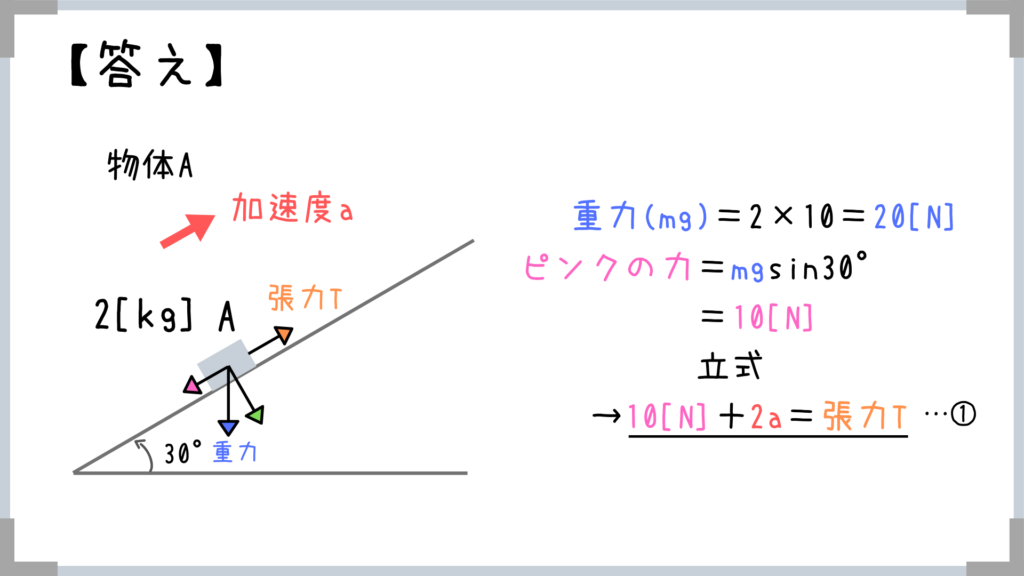
慣れてない方は「三角比を使った分解法」で1:2=□:20[N]とおいてやってもOKです!
物体それぞれにはたらく力をきちんと図示することが大切です。
このページを閉じたいと思います。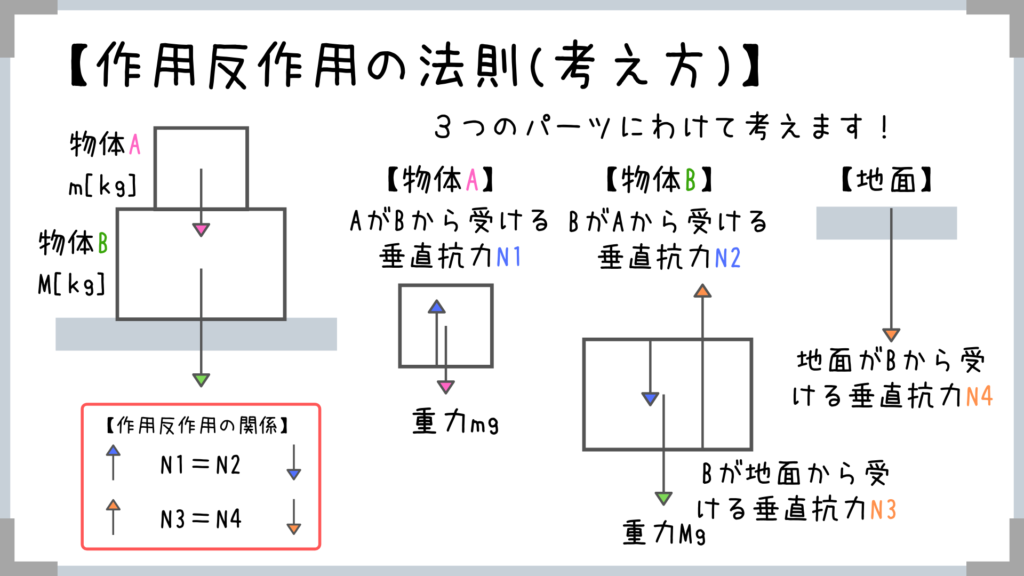
「1つずつ丁寧にはたらく力を図示」することが大切です!
今回はタテ方向の力で作用反作用の法則の紹介をしましたが、コレは横向きに力がはたらいている場合も同様に考えればOKです!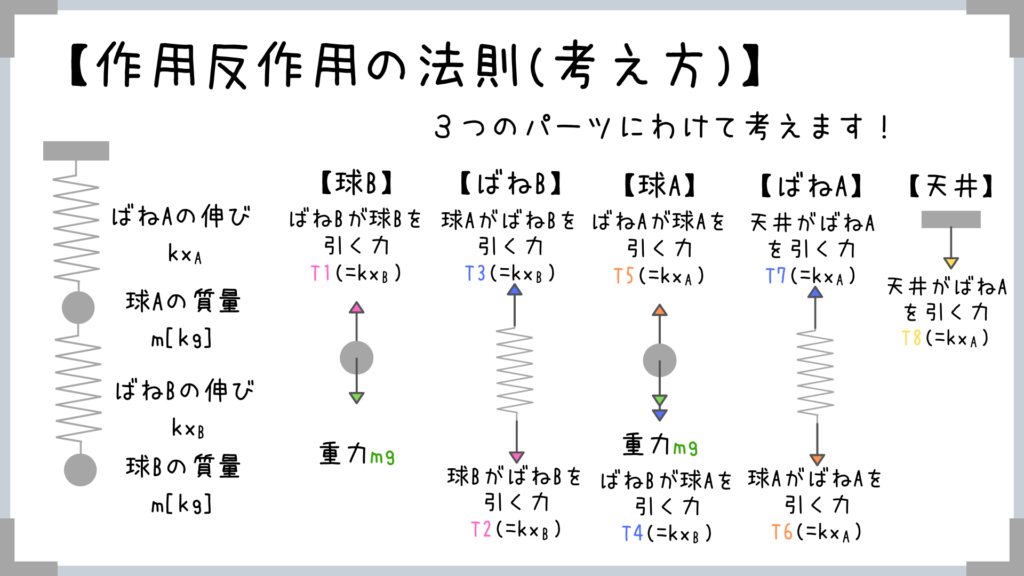
重要度が高い分野なので、説明も長くなってしまいました!
とにかく重要なのは
わからないことがあれば
私のLINEで気軽に質問してみて下さい
![公務員のライト[試験情報データベース]](https://senseikoumuin.com/wp-content/uploads/2022/12/cropped-logo-color-2.png)
















今は公務員試験のせんせいとして、受験生の皆さんに物理が基礎となってる構造力学や水理学、土質力学なんかを教えています。
このページは『物理初心者の文系の方』に向けて書いたものです!
もちろん教養試験対策だけじゃなくて技術職の人の工学の基礎対策にもなると思います!
じゃあみんなが苦手な力学分野の対策スタート(^o^)/