東京都庁・特別区で超頻出!
電気と磁気の問題は地方上級・都庁の試験で頻出です!
しかも、特別区に関してはほぼ毎年出題されているんですね!
→直近10年でも平成26年以外、この電気・磁気分野から出題されています!
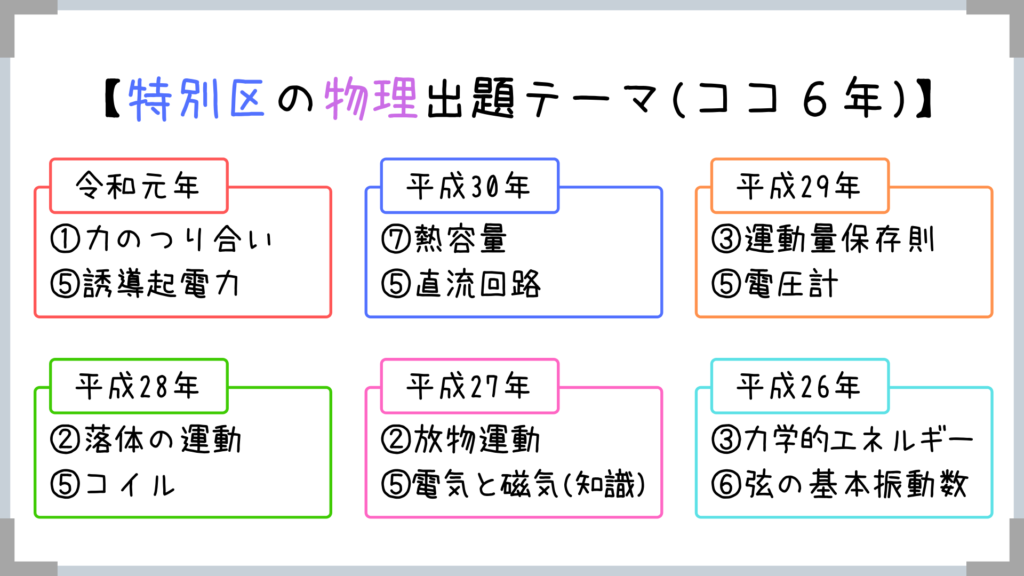
特別区のココ6年の出題テーマですが、⑤の電気・磁気分野から出すぎ…ですよね!!
ちなみに東京都庁もココ3年中2問は電気・磁気分野からの出題です!
公務員試験の物理分野で一番頻出なテーマと言っても過言ではありませんよね~!
主には公務員試験の物理対策として、
中学~高校の物理の分野すべてを解説していきますが、
もちろん中学生高校生の方が見ても参考になると思います!
ではさっそく【電気と磁気】分野の勉強をしていきましょう!
- ①力のつり合い
- ②物体の運動
- ③エネルギーと運動量
- ④周期的な運動と慣性力
- 今ココ→⑤電気と磁気
- ⑥波動
- ⑦熱と原子、その他

目次
【電気と磁気】初心者向けに3項目を解説!
公務員試験ではこの3つのテーマの中でも出題されやすいポイントが決まっています!
特に「電気回路」の問題が多いので、基礎的な部分はきちんとおさえておきましょう!
もし物理に拒絶反応を感じてしまっている方でも、直流回路の問題は理解しやすいのでココだけ勉強しておくのはアリだと思います!
私が物理苦手だったとしても、直流回路の問題だけはきっとおさえておくと思います。
では、本編にまいりましょう!

別に難しい話ではないので、サクッと勉強して問題に慣れていきましょう!
【電流・電圧と電気抵抗】基礎が理解できてないとお話にならない!
いきなり問題を解いても、理解に苦しむと思います。
まずは電流・電圧と電気抵抗の公式や考え方、性質について簡単に勉強していきましょう!
オームの法則から紹介していきますが、コレは中学校の時の理科の教科書に載っているレベルなので、理解するのも簡単だと思います!
オームの法則って何だって考えるよりも、この公式を覚えてしまった方が早いと思います! 「電圧=抵抗×電流」ということ! そして、抵抗Rというのは電流の流れにくさ、 電気抵抗あると邪魔で水はまっすぐ進めないって覚えておくといいかもしれません。 そして、抵抗の両端に加わる電圧RI[V](落差)を抵抗による電圧降下と言います。 ぶっちゃけコレを使った問題はほとんどでません。 無理に覚えなくてもOK! 参考書に書いてある表が見やすいという方はそのまま覚えてもらって構いませんが、私は覚えにくいと思います! そして、並列接続の部分は例えば10mの幅の水路を7mと3mに分けただけといった感じで、合計の幅は一定だと考えておきましょう! 公式を丸々暗記するんじゃなくて、この水路をイメージすることが大事だと私は思います! 並列接続の合成方法だけは覚えちゃった方がラクかなと個人的に思います。 今回は『抵抗の合成法』を教えるのが目的なので、直列と並列それぞれ紹介してみました! もちろん、並列の部分を消した段階で「電圧降下」に着目して解くのもアリですよ! 最初の抵抗のところでは20V電圧降下しますよね? 電気回路というのは色々な解法があって面白いですよ! 物理の世界で大事なのは自分が〇〇になってみること… そう、キルヒホッフの法則というのは「自分が電流になろう」って考え方のことです! 電源でもらえる電圧の値と、抵抗で失う電圧の合計は等しいハズですよね! コレだけですね! まったくそんなことありません! ①まずは電流の大きさと向きをすべての位置に図示していきます! ②次にどのルートでもいいので、1周まわるルートを決めます。 最初に50Vあったものが、抵抗を通り過ぎた段階で0Vになっていなければいけませんよね! やることはコレだけです。 並列の時は、電流の進む量は抵抗の大きさに反比例するっていう考え方ができるのかどうか問う問題がよく出ます。 そして、ジュール熱というのは抵抗による発熱量のことなんですが コレも水路でイメージしちゃった方が理解が早いと思います。 物理で大事なのは「イメージすること」ですよ~! もう一度復習がてら、「電気回路=水路」の状況をまとめてみましょうか! 電圧Vというのは、水が落ちる高さのことでしたよね? じゃあ電力は…エネルギーですから、「水が落ちる高さ×流れる水の量」のことですよね? 水路をイメージしておけば公式で迷うことはなくなると思います! 簡単すぎますね! そして、水の流れ、要は「水の流量」の単位というのは[m3/s]であらわされます。 実はアンペアの単位というのは、「1秒間に1クーロンの電荷が移動するときの電流の大きさ」のことなんですね! 水というのは水の粒、電気というのは電子の集まり… ココで求めたエネルギー(電力)は1秒あたりの電力ですから、 こんな超シンプルな消費電力の問題が実際に特別区で出てるんですよ~! 電流の大きさがわからないので、ここを求めていきたい。 ごちゃごちゃしていて理解しにくいテーマかもしれませんが、ココは主に知識系の問題が多く、計算系の問題は少ないですから、文系の方も対策はしやすくなっていますよね! ココだけはおさえておけってポイントは みんなもコレは聞いたことあるんじゃないかな? では、まずは基礎的な部分から紹介していきますね! 覚えておいた方がいい知識だけまとめておきます! 磁石を置いて、その横に鉄の球を置く。 N極からS極を線で結ぶ 磁気量(磁極の強さ) 磁極と磁極の間にはたらく力を磁気力(磁力)っていいますよね! そして、磁場と同様に、電気力を及ぼす性質を持つ空間を電場(電界)と言います。 ちょっと文系の方は慣れないかもしれませんが、N極とS極や電荷を帯びた2つの粒子などの間にはひきつけあったり、反発しあったりする力がはたらくんですね! まぁ公式の形だけ覚えておけばOKかなと思います。 磁場の向きは『右ねじの法則』を使って求めていきましょう! 直流電流の場合と、コイルの場合で右手の使い方が逆になるので注意が必要! 例えば、直流電流による磁場の場合、 例えば、右側の例で力の方向が隠れていた場合 電磁誘導…難しそうですよね! 簡単に言うと、コイルに磁石を近づけたり遠ざけたりすることによって電気を流すことを電磁誘導と言います! そして、この誘導電流によって生じる電流のことを誘導電流と言います。 自転車に乗っている時にタイヤの回転に合わせて光るライトってありましたよね! すべて覚えようとすると効率が悪いですから、もうコレ知識として覚えちゃいましょう! 「N極が攻撃している」って部分を軸に考えておけば、電磁誘導の問題は楽勝♪ 電磁誘導の磁場は「N極の攻撃に対抗する」と覚えて下さい! この画像を覚えておくだけで公務員試験にでてくるレンツの問題はすべて解けると思いますよ! このパターンを基準にしておけば、あとはすべて反対だと覚えておけば電流の向きも磁場の向きも迷うことはないでしょう。 そして、S極の動きもN極の動きの反対! どうでしょうか、1つ基準を作って後はすべて反対だと覚えておけば簡単じゃないですか? 一応、本来のレンツの法則についての紹介もしておきますね! 電磁誘導はコイルを貫く磁力線の本数の変化を妨げる向きに流れる 誘導起電力の大きさを大きくするためにはどうするか… 全然、難しい話じゃないですよ! 単純にコイルを強くすれば電気も大きくなりますし、磁石を強くすれば生じる電気も大きくなりそうですよね! ファラデーの法則というのはこの関係を式で表しただけです! 一応、式の形と先ほど紹介した誘導起電力の大きさを上げる3つのポイントはおさえておいたほうがいいと思います。 特別区で平成28年に出題されているのでサクッと紹介! コイルというのは自分自身に流れる電流Iによって電磁誘導を起こすんですね。 次にコイルが蓄えられるエネルギーについて紹介します。 結論から言うと 詳しく紹介すると、電圧と電流の関係は また、電流Iというのは単位時間(1秒)あたりに流れる電荷qの量のこと そして、電機分野における仕事量Wというのは「W=q(電荷)×V(起電力)」であらわせます。 →代入すると「W=L×IdI」 ちょっと難しい話になってしまうので、技術職志望の方以外は捨て問ですね。 これで「電気・磁気」分野の紹介は終わりです! 根本まで覚える必要はないので、広く浅く対策しておきましょう! 長々とお疲れ様でした! 
【オームの法則とは?】超重要だから絶対に覚えよう!

「V=RI」
はい、超簡単ですよね!
電流Iというのは電気の流れのことですよね!
→抵抗を水車、電流を水路(水流)だと考えてみるとイメージしやすい!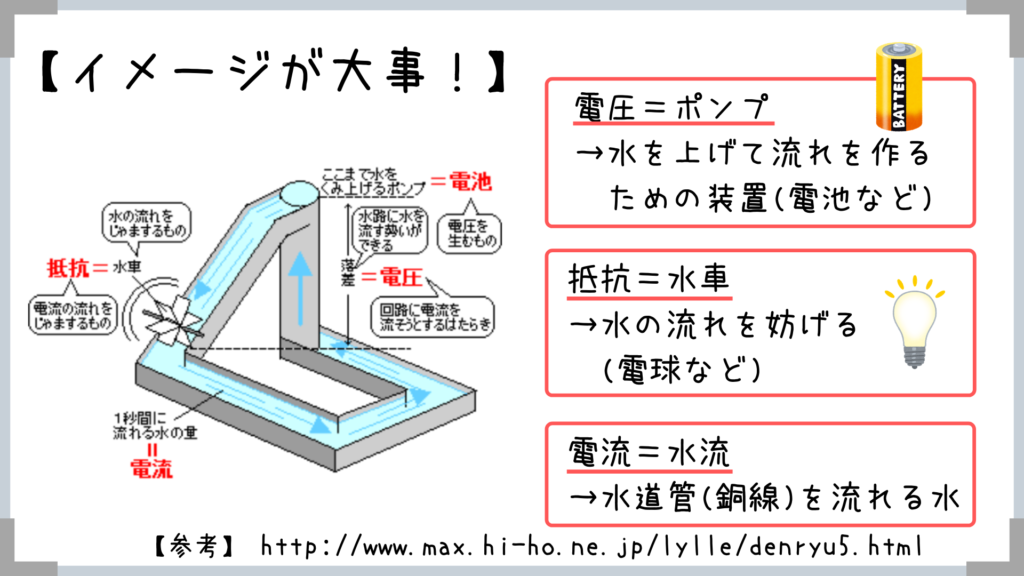
→水を通すためには落差が必要!
例えば、抵抗が2個ある↓のような回路があった場合、「抵抗によって電圧が降下する」というイメージ!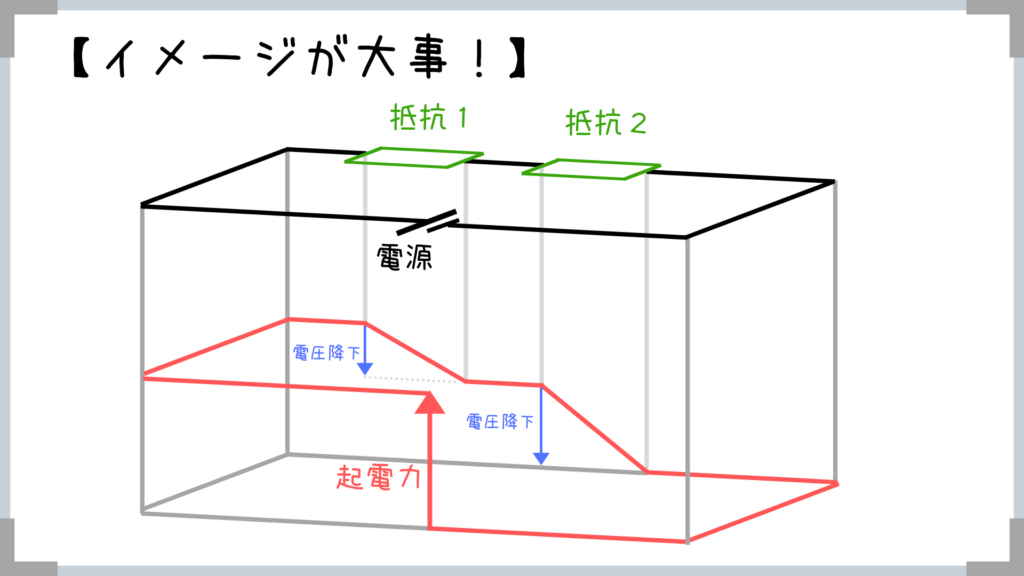 ※電源の棒が小さい方から大きい方に電流が流れます!
※電源の棒が小さい方から大きい方に電流が流れます!
1[C]の電荷が持つ位置エネルギーを電位というんですが、この2点間の電位の差を電圧というんですが、わざわざそんな難しく覚える必要はありません!
こうやって図で覚えたら簡単でしょ~?【抵抗の性質】重要度低!
銅線の抵抗Rは導線の長さLに比例し、断面積Sに反比例します。
低効率をρとすると、「R=ρL/S」とあらわせます!【抵抗の合成・性質】重要すぎる!絶対に覚えましょう!
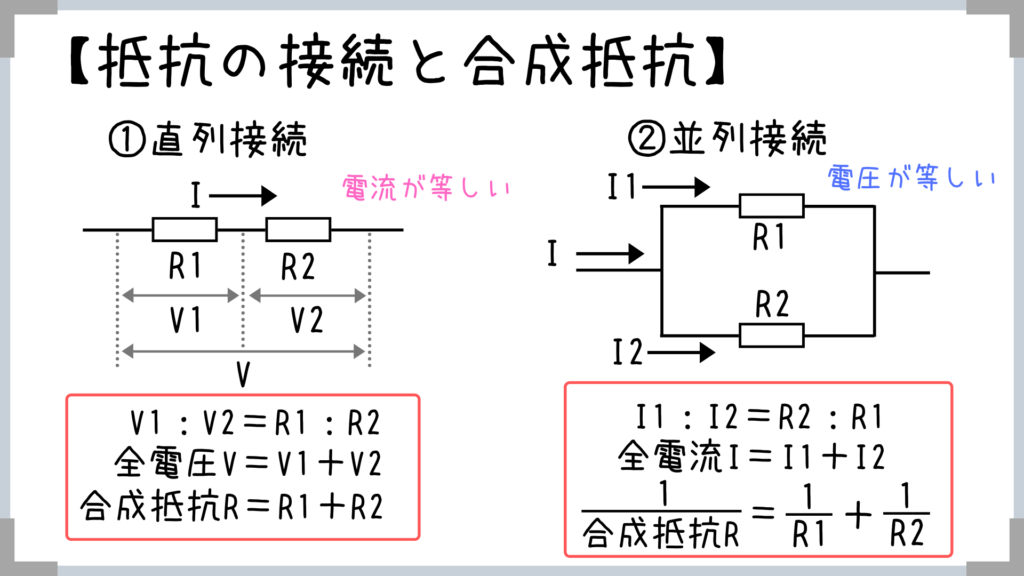 先ほど、回路は水路であらわすとイメージしやすいと言いました!
先ほど、回路は水路であらわすとイメージしやすいと言いました!
この水路の大きさ・幅というのはどの点でも等しいと覚えておきましょう!①直列接続の合成抵抗・性質
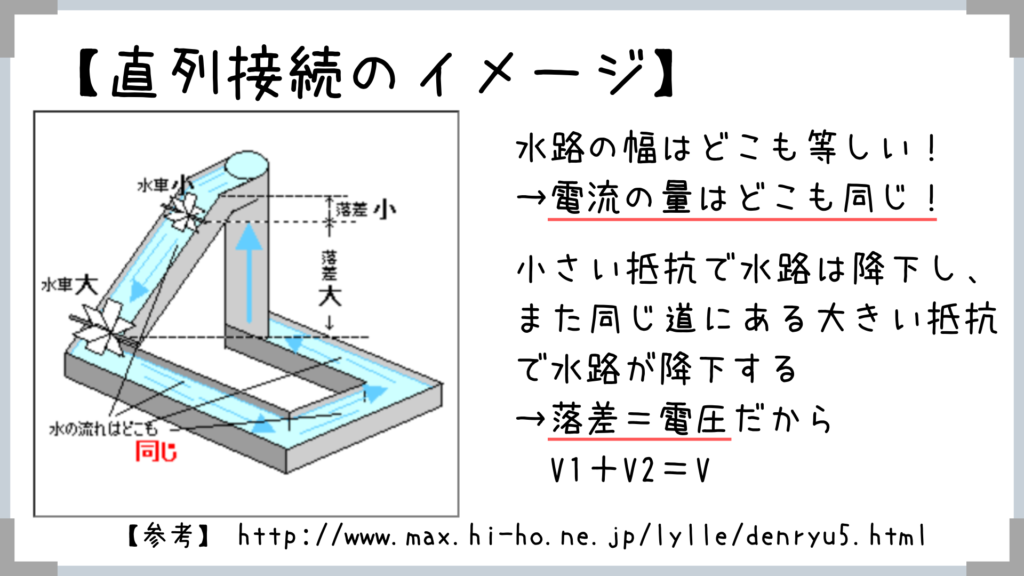
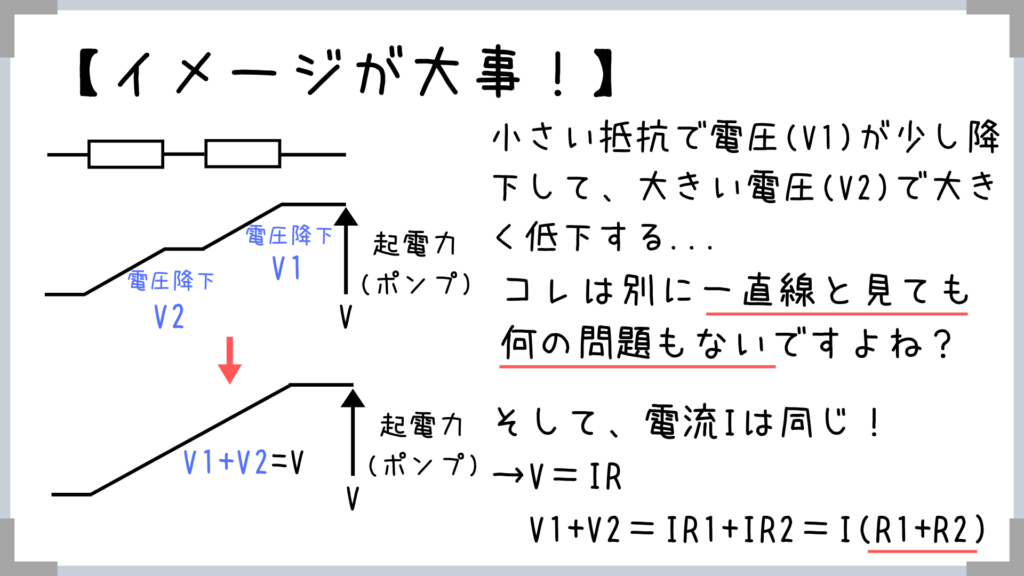
水路をイメージ出来れば、電流がどこも同じなんてすぐにわかりますし、電圧(落差)を一直線に見ていい、抵抗も単純に足すだけってすぐにわかっちゃいますよね!
②並列接続の合成抵抗・性質
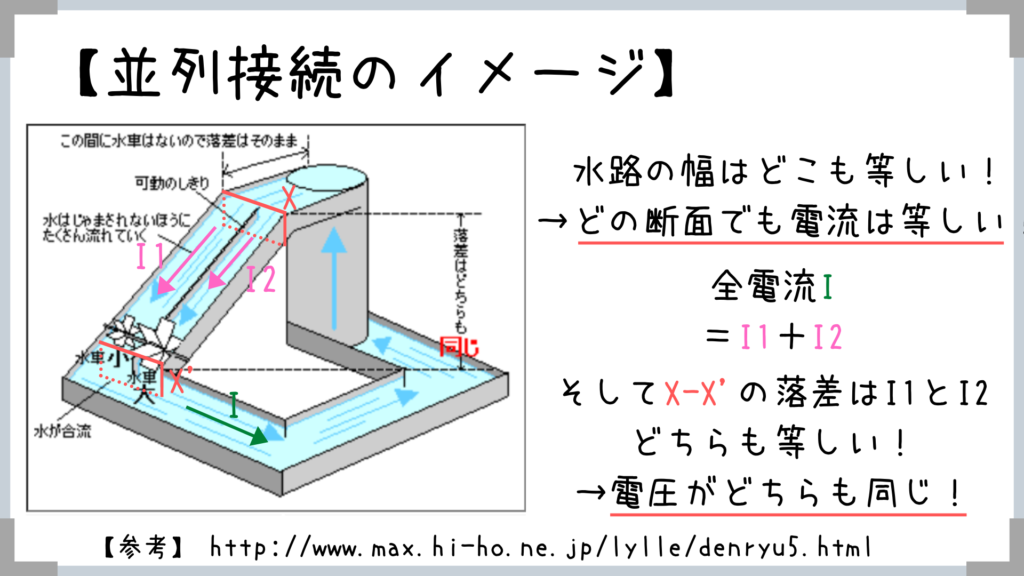 この水路を暗記しておけば、水路の幅が一定だからI1とI2を足したら全電流Iになる、落差(電圧)はI1の方とI2の方どちらも同じってすぐにわかりますよね!
この水路を暗記しておけば、水路の幅が一定だからI1とI2を足したら全電流Iになる、落差(電圧)はI1の方とI2の方どちらも同じってすぐにわかりますよね!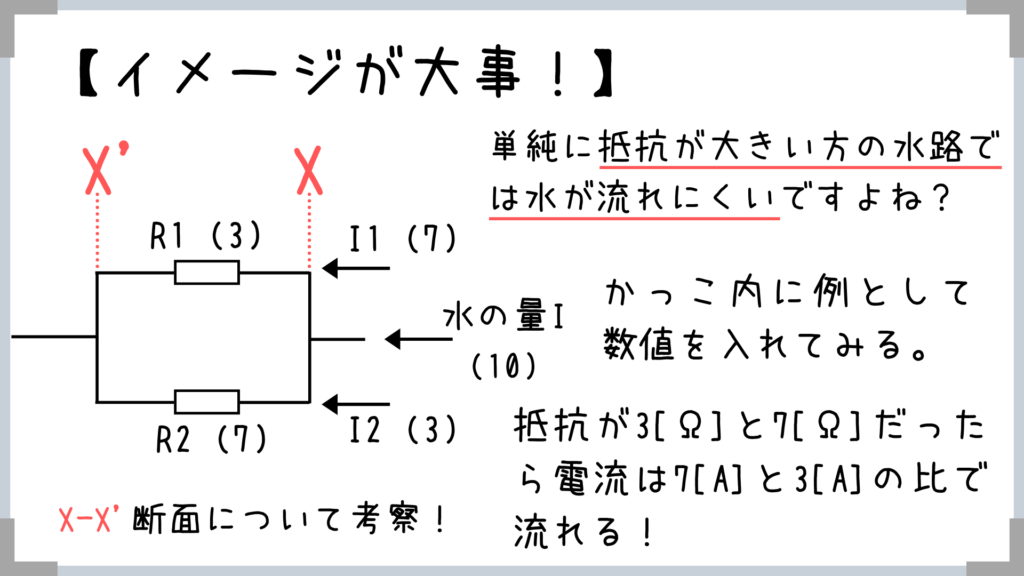 そして、水っていうのは邪魔されない方にたくさん流れていきますよね!
そして、水っていうのは邪魔されない方にたくさん流れていきますよね!
その流れていく水の量というのは抵抗の大きさに反比例します!
→I1:I2=1/R1:1/R2=R2:R1
→電圧V(落差)がI1・I2どちらも一定なので、V=IR=I1R1=I2R2から式を求めてもOK。【抵抗の合成問題】1問解いてみよう!
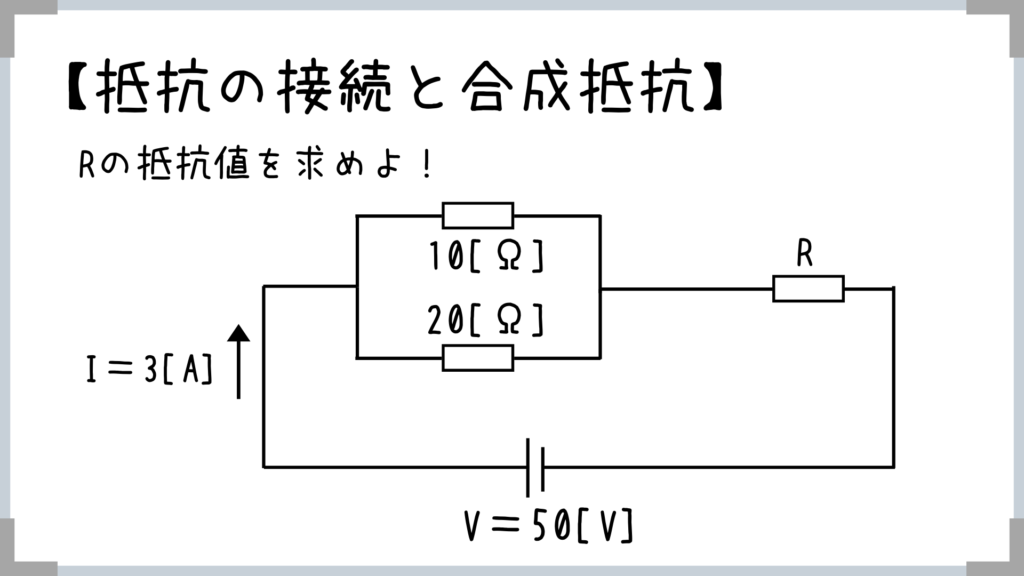 ここまでの基礎知識を駆使して、右側の抵抗値を求めてみましょう!
ここまでの基礎知識を駆使して、右側の抵抗値を求めてみましょう!
まずは「並列部分の抵抗の合成」からですよね!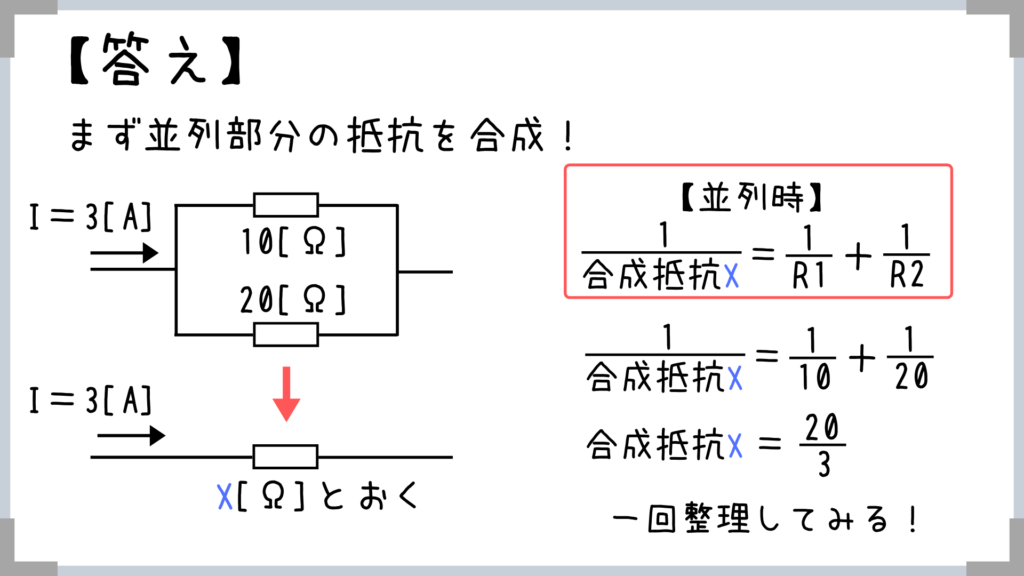 並列時の抵抗の合成は非常によく使うので、絶対にマスターしておきましょう!
並列時の抵抗の合成は非常によく使うので、絶対にマスターしておきましょう!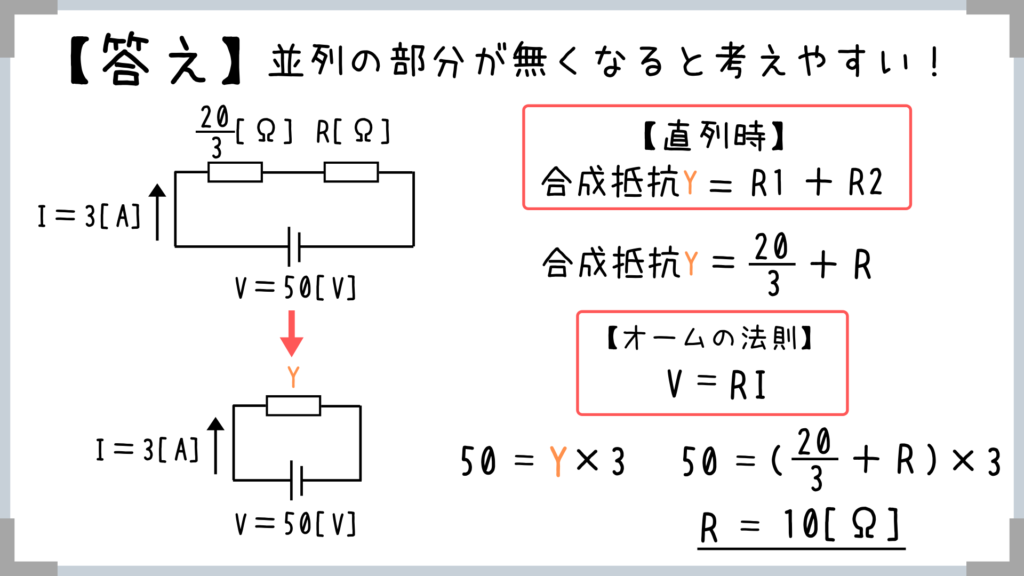
どうでしょう、簡単でしたか?
ということはもう1つの抵抗のところでは30V電圧降下するハズです!
そして水路の幅も一定なはずです!
→電流はどこも一定(3[A])
→ココでオームの公式を立てれば一瞬ですね!
【オススメ】キルヒホッフの法則!
実は先ほどの問題、ほとんどの方が抵抗を合成して解くと思うんですけど、慣れてる方は「キルヒホッフの法則」というのを使うんですね!
→キルヒホッフの法則を使いこなせればこんな問題一瞬で解けちゃいます。
(もちろん、興味が無い方はこの項飛ばしてもOKです)
(当然厳密にいうとそういうことではありませんよ!)
ということでやることをまとめてみるとこんな感じ↓
「ん?なんか難しそうって?」
実際に解いていきますね!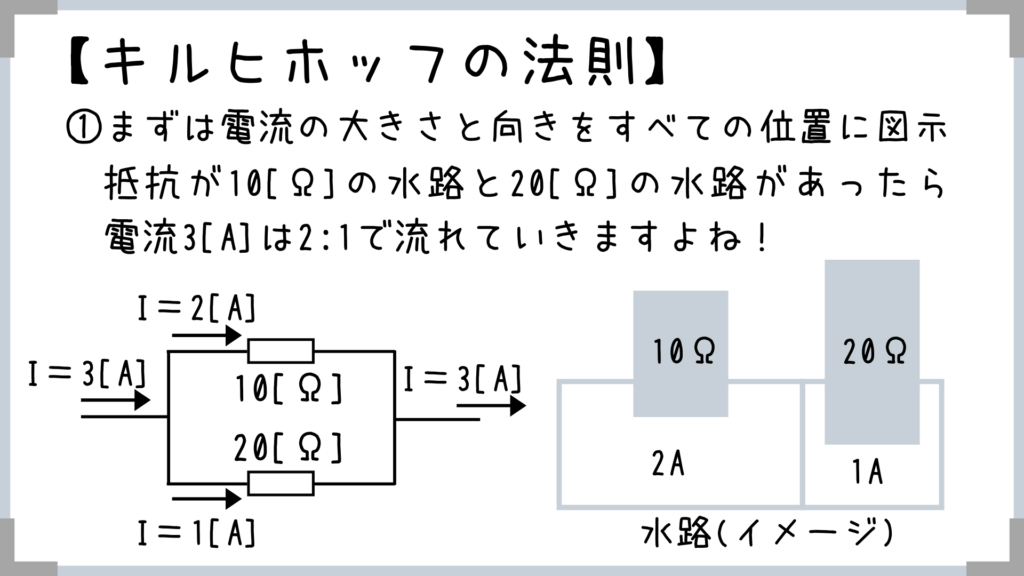 ※右の図は西から東を見た時の水路の断面を表してます。
※右の図は西から東を見た時の水路の断面を表してます。
(文字で置く場合は向きは適当でもOKです。もし方向が違ってたらマイナスがつくだけですからね)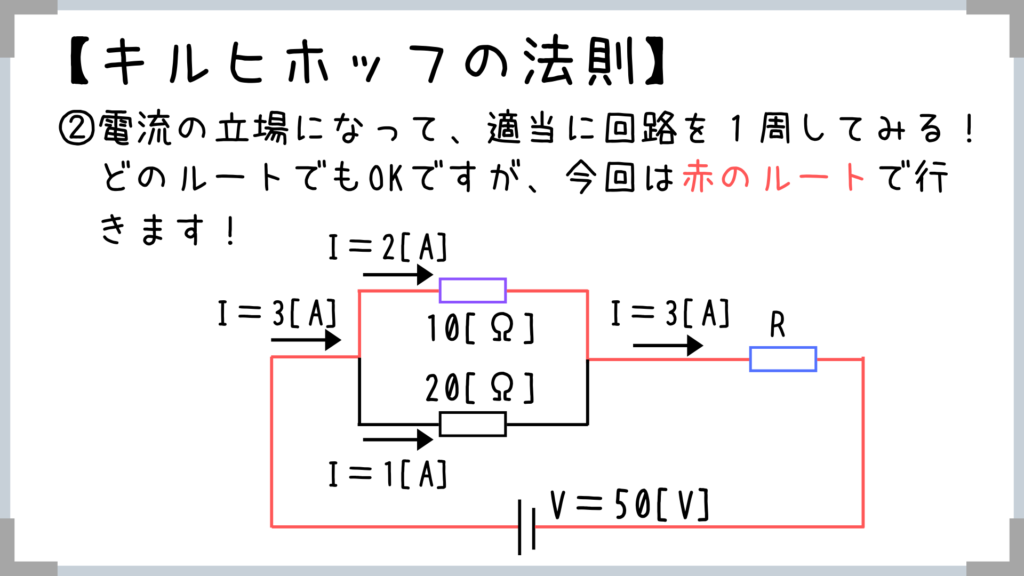
(並列の部分は電圧は等しいというのがポイント)
紫の部分と青の部分で電圧を失いますよね!
③ということでもらう電圧と失う電圧を等式で結ぶ!
④計算する!
慣れると超簡単ですよ~!
水路をイメージすれば、並列時も電圧が一定なので、Iが大きかったらRは小さくなければいけない、Iが小さかったらRは大きくなければいけないと、すぐに気づくことができると思いますので、やっぱり水路は超オススメ!
この問題で紹介した「水路のイメージ」を大事にしていただきたいなと思います。
なんせ考えやすいので勉強時間短縮になりますよね!
皆さん頑張って覚えて下さいね!【消費電力と電流による発熱(ジュール熱)】コイツも水路でイメージできちゃう!
 消費電力というのは、単位時間(1秒)あたりに消費されるエネルギーの量のことですね!
消費電力というのは、単位時間(1秒)あたりに消費されるエネルギーの量のことですね!
単位はW[J/s]です。
単純に消費電力[J/s]に時間[s]をかけてエネルギー[J]を出したもののことです!【消費電力とは?】実際にイメージしてみよう!

そして、電流Iというのは流れる水の量のこと。
→P=VI
→1秒間に移動する水粒子の大きさ
→電気も粒(電子)
要は水も電気も同じように考えてOKということです。
コイツに時間をかければエネルギーの大きさを計算することができるわけです。
→P×t=Q(発熱量)
でも大事なのは問題が解けるかどうかなので、公式を覚えた方がラクだったらもちろんそれでもOKです!
ということで実際に特別区の問題を1問解いてみましょう!【消費電力と電流による発熱(ジュール熱)の演習問題】
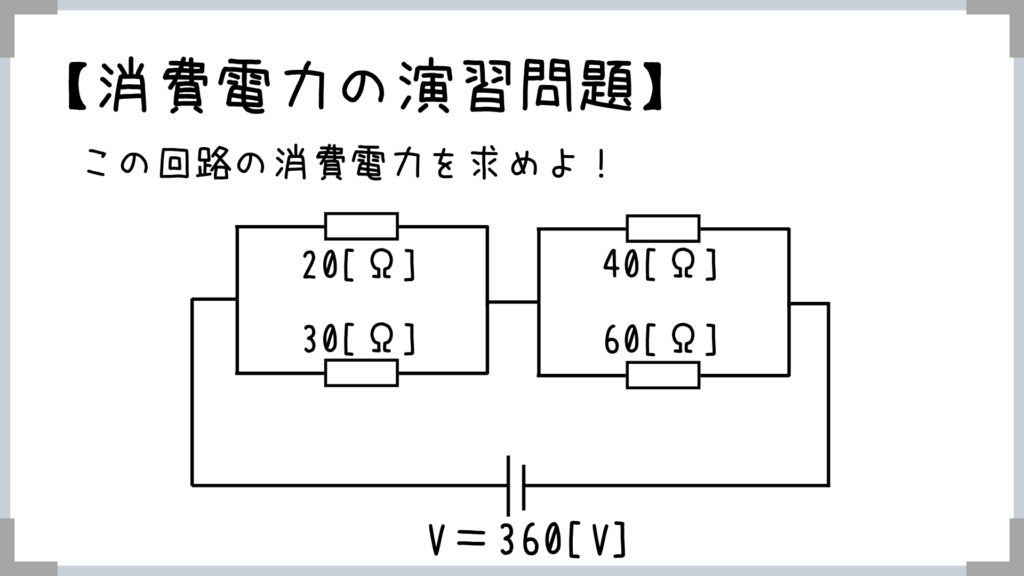
コレは落としてはいけませんよね!
→まずは抵抗の合成ですね!
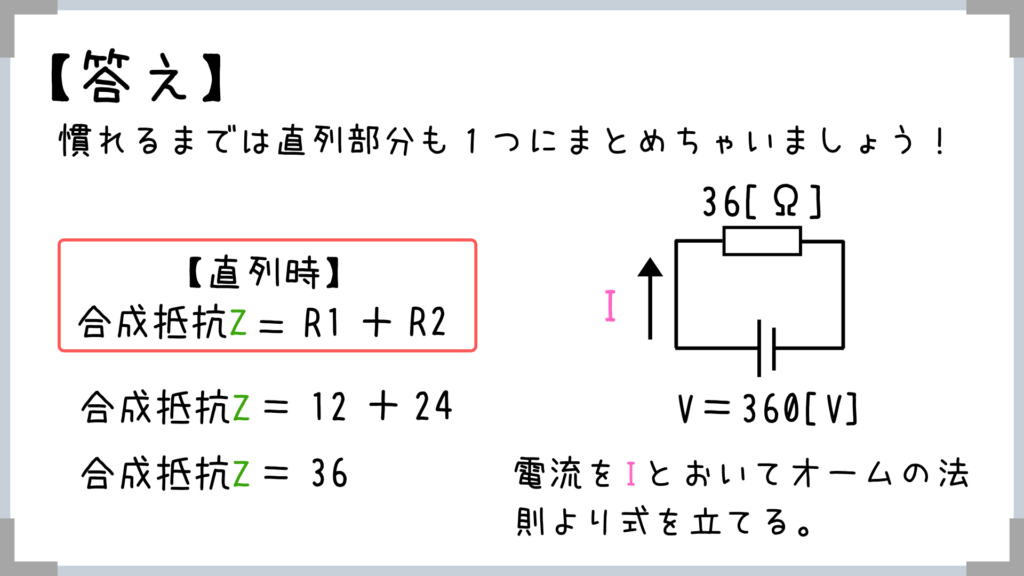 もちろん、並列合成だけやって電流Iを求めに行ってもOKですが、慣れるまでは並列も直列も抵抗は1つに合成しておくようにしましょう!
もちろん、並列合成だけやって電流Iを求めに行ってもOKですが、慣れるまでは並列も直列も抵抗は1つに合成しておくようにしましょう! 合成して、公式に当てはめるだけですから簡単ですよね!
合成して、公式に当てはめるだけですから簡単ですよね!
360V分の落差(電圧)があって、水の量は10A(電流)ですから、かけあわせて3600[W]が答えです。【磁気分野】基礎的な部分だけおさえておきましょう!
とはいってもめちゃくちゃ大事かといわれるとそうでもないので、ほどほどに頑張っていただけたらなぁと思います。
「右ねじの法則」と
「フレミング左手の法則」ですね!【磁石による磁場】基礎が理解できてないとお話にならない!
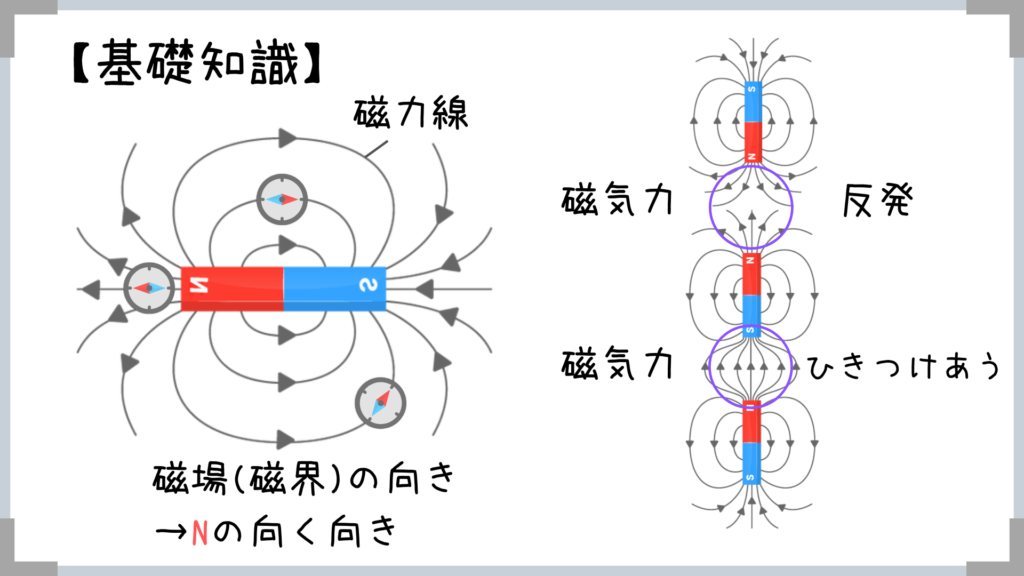
→引っ張られる!
→磁石の力がはたらく空間を「磁場(磁界)」という!
→これを磁力線という
→N極の向き=磁力線の向き
→単位は[Wb(ウェーバ)]
コイツの大きさも求める公式があったりするんですね!
→基本的な性質は磁場も電場も同じなので、「正電荷=N極」だと思っておけば、公務員試験で困ることはないです!【磁気力のクーロンの法則】磁石間にはたらく力!
出題頻度は低いかもしれませんが、令和元年度の特別区の試験で「誘導起電力(ファラデーの法則)」というマイナーな分野からの出題があったので、クーロン力についても一応、おさえておいた方がいいかなと思います。 (※静電気力のクーロンの法則が有名なので、文字はあえてqとおいておきました)
(※静電気力のクーロンの法則が有名なので、文字はあえてqとおいておきました)
技術職の方は使いこなせればダメですよ~!
こちらはまた別ページで解説します。【電流が作る磁場(重要)】右ねじの法則を使いこなそう!
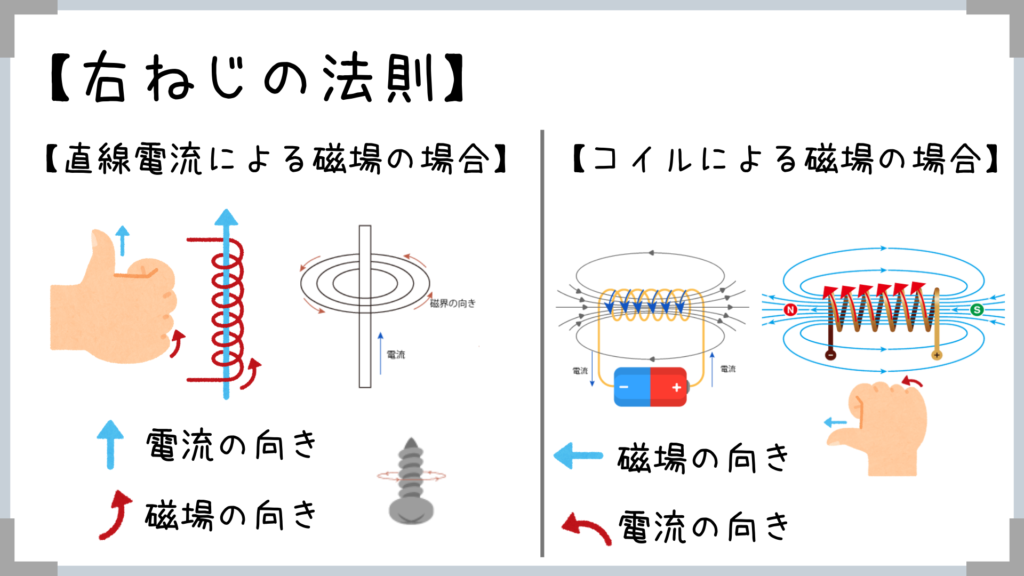
→基本的には直流電流のほうを基盤として覚えておけばOK!
→当然、普通にコイルの場合は磁場が親指って覚えてもOK!
電流の向きがわかっていたら右手の親指を電流の向きに合わせれば、
ねじの回転方向(ねじを時計回りに回転)が磁場の向きとなります。
【電流が磁場から受ける力(重要)】フレミング左手の法則も頻出!
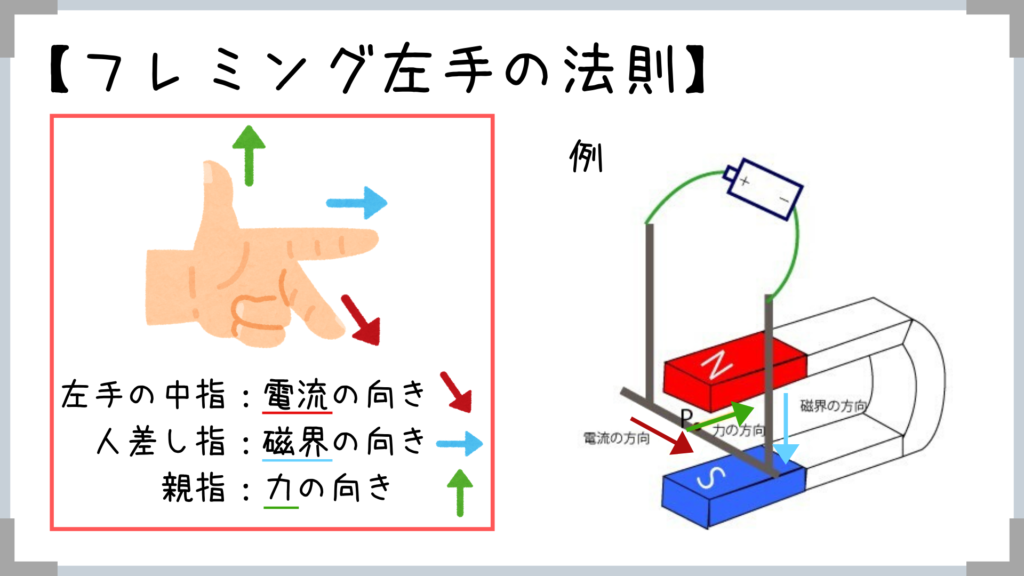 コレは超有名ですよね!
コレは超有名ですよね!
皆さんも聞いたことがあるのではないでしょうか。
多分、昔は理解していたと思うのですが、今どんなものか聞かれても思い出せませんよね(汗)
ココは公務員試験でも頻出なので、絶対に覚えておきましょう!
左手の中指を右下に
左手の人差し指を下にすると
親指は右奥側に向くので
親指の方向に力がかかっているんだなってすぐにわかっちゃいます!【電磁誘導】レンツの法則とファラデーの法則
でも難しいのは名前だけ!
→早く磁石を動かすと電気は大きくなり、磁石を静止させると電気は発生しない。
→磁界を変化させることによって電気を発生させている!
実はこれも同じメカニズムで電気を発生させています。【レンツの法則】N極は攻撃している!
(レンツの問題もそこそこ出題されてますが、根本を理解していなくても解ける問題ばかり)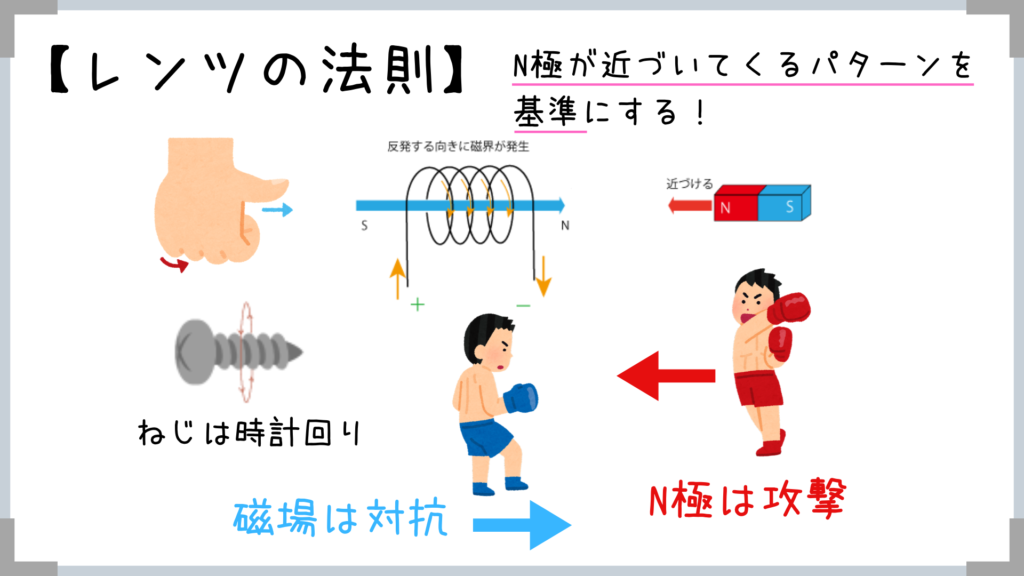
例のようにN極が近づいてきたら、磁場は反発する向き(右向き)にはたらきます。
ココで「右ねじの法則」を使えば、電流が+という表記の方から-という表記の方に向かって進んでいるのがすぐにわかると思います。
N極が遠ざかる
→磁場も遠ざかる(左)
S極が攻撃してくる
→磁場は遠ざかる(左)
S極が遠ざかる
→磁場は攻撃する(右)
語呂で覚えるような感じで覚えやすいように覚えていきましょう!【ファラデーの法則】単純な話です。
あとは出し入れする速度についてですが、例えば、手動で動かす懐中電灯ってありますよね!
早く動かせば動かすほど、ライトも強く光ると思います。 公務員試験においてはこの公式まで覚える必要はないと思うのですが、令和元年度の試験ではこのファラデーの公式を利用して解く誘導起電力の問題が実際にでました。
公務員試験においてはこの公式まで覚える必要はないと思うのですが、令和元年度の試験ではこのファラデーの公式を利用して解く誘導起電力の問題が実際にでました。
この公式をただ利用して解く超簡単な問題でしたけどね。【コイル】自己インダクタンス
そして、この誘導起電力がコイルの電圧となります。
→コイルには電流Iに比例する磁束Φ=LIが発生する!
→この比例定数Lのことを「自己インダクタンス」と言います。
知識として、
「コイルに蓄えられるエネルギー=1/2×LI2」
と覚えておけばOK!
「V=L×dI/dt」とあらわせます。
→dI/dtというのは単位時間あたりに流れる電流Iの変化量
→単位で表すと「I=dq/dt」
→とある時間に流れる電荷の量というの「q=Idt」とあらわせる。
(電力P=VIと同じ原理)
→積分して「W=1/2×LI2」
(まぁ技術職志望の方も結果だけ覚えておけばOK!)
![公務員のライト[試験情報データベース]](https://senseikoumuin.com/wp-content/uploads/2022/12/cropped-logo-color-2.png)
















今は公務員試験のせんせいとして、受験生の皆さんに物理が基礎となってる構造力学や水理学、土質力学なんかを教えています。
このページは『物理初心者の文系の方』に向けて書いたものです!
もちろん教養試験対策だけじゃなくて技術職の人の工学の基礎対策にもなると思います!
超頻出テーマなので、文系の方もココだけは頑張って勉強しておきましょう!