LINE公式にご登録頂くと、自動的に「裏技・テクニックまとめ」が送付されます。
[/box]目次
判断推理
一筆書き
例題
次の図形は一筆書きができるか。
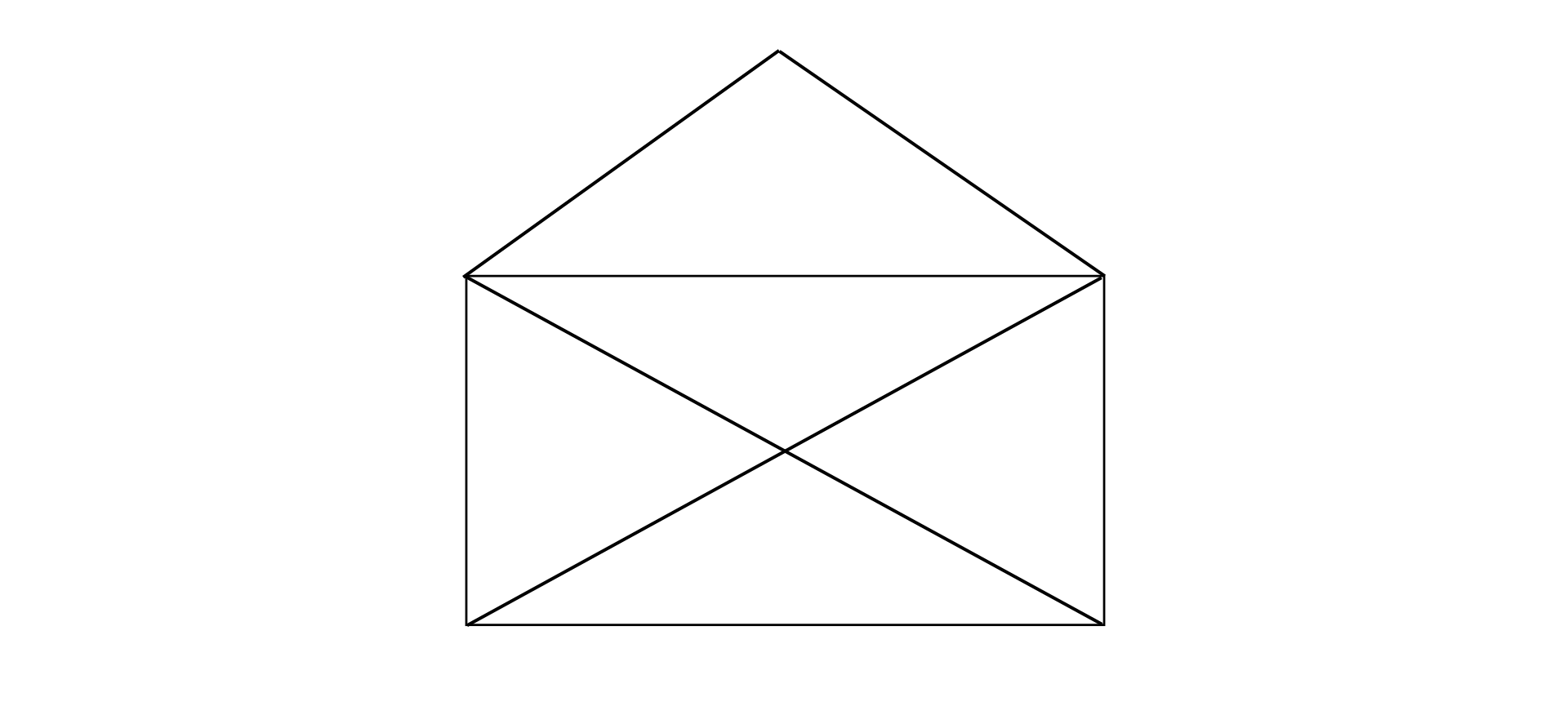
一筆書きできる図形の見つけ方
奇数の交差点とは、
〇のように線の数が奇数(3)か所の交差点のことを指します。
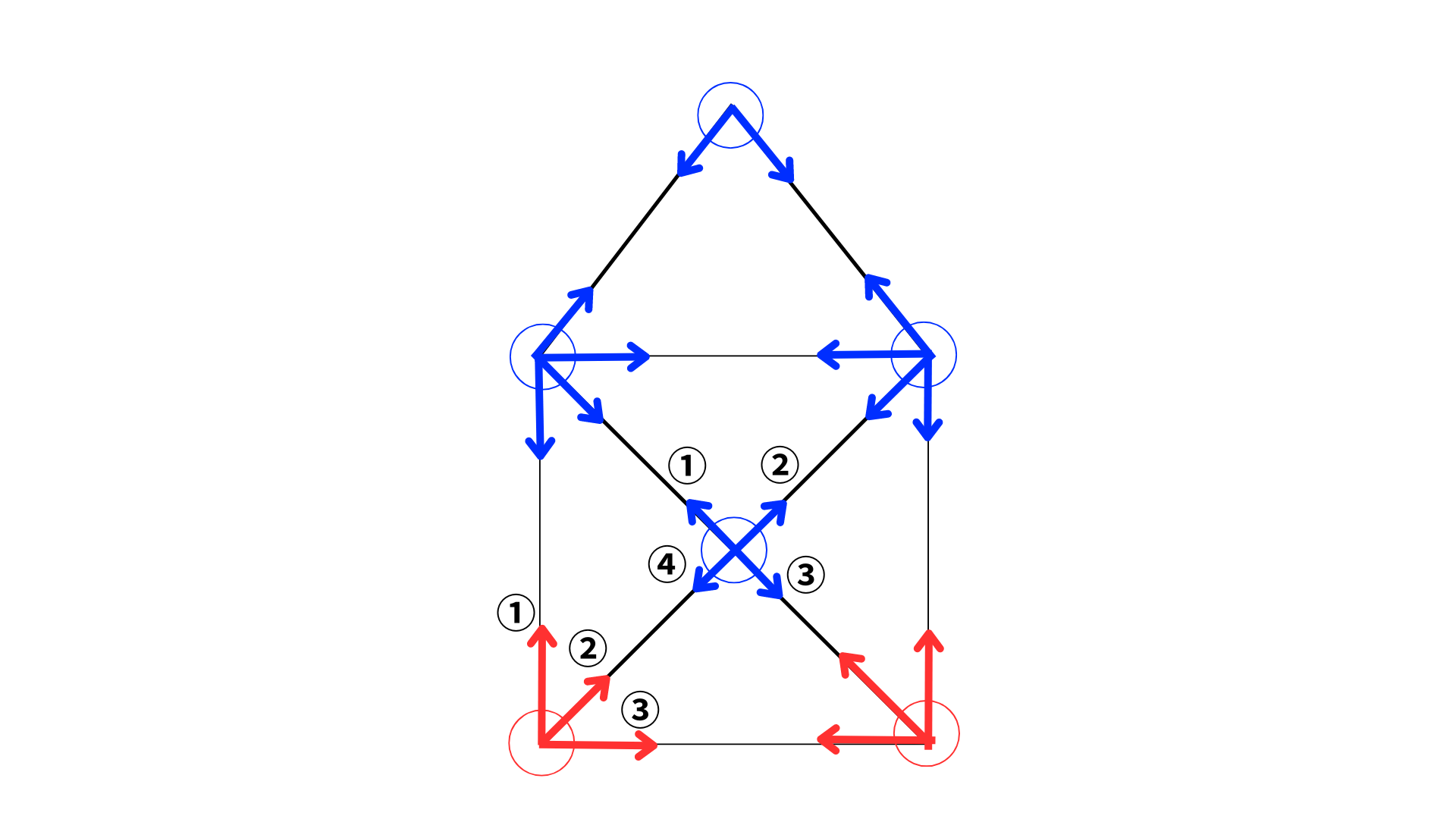
例題の解説・解答
例題は奇数の交差点が2か所あるので一筆書きができる図形です。
船渡り
例題1
子どもは2人同時に乗れるが大人は1人しか乗れない小舟を1そうだけ使って、同じ岸にいる大人3人と子ども4人が川を渡るとき、全員が反対側の川岸まで渡り終えるのに必要な移動の最小回数として、最も妥当なものはどれか。ただし、移動手段は小舟のみで、小舟に大人と子どもが同時に乗ることはできず、小舟による一方の川岸から反対側の川岸までの1度の移動を1回とする。また、小舟で移動するには、大人3人と子ども4人のうち、最低1人が小舟に乗らなければいけないものとする。
- 1. 15
- 2. 16
- 3. 17
- 4. 18
- 5. 19
本来の解き方
以下のようなプロセスを経て、全員が渡ることになる
| ① | 子ども2人渡る | ② | 子ども1人戻る |
| ③ | 大人1人渡る | ④ | 子ども1人戻る |
| ⑤ | 子ども2人渡る | ⑥ | 子ども1人戻る |
| ⑦ | 大人1人渡る | ⑧ | 子ども1人戻る |
| ⑨ | 子ども2人渡る | ⑩ | 子ども1人戻る |
| ⑪ | 大人1人渡る | ⑫ | 子ども1人戻る |
| ⑬ | 子ども2人渡る | ⑭ | 子ども1人戻る |
| ⑮ | 子ども2人渡る | ⑯ | 子ども1人戻る |
| ⑰ | 子ども2人渡る |
このように、2人で行って1人が戻ったり、大人が行って子どもが戻ったりを繰り返し、計17回で全員が渡ることができる。
船渡りの解き方
例題1の解説・解答
① 大人と子どもの人数を確認する。
今回の問題は大人3人、子ども4人
② 公式に当てはめて計算する。
3×4+4×2-3=12+5
=17(回)
例題2
川があり、大人6人、子ども3人が、スタート地点がある一方の岸から、ゴール地点がある対岸まで、1そうの足こぎボートを使って以下のルールに従い移動する。スタート地点からゴール地点までの移動、ゴール地点からスタート地点までの移動をそれぞれ1回と数えるとき、全員が対岸のゴール地点まで移動し終えるまでのボートの最小の移動回数として、最も妥当なものはどれか。
<ルール>
・ボートに大人は1人だけしか乗ることができない。
・ボートに子どもは最大2人までしか乗ることができない。
・ボートに大人と子どもが同時に乗ることはできない。
・ボートが無人で移動することはない。
- 1. 23回
- 2. 25回
- 3. 27回
- 4. 29回
- 5. 31回
例題2の解説・解答
①大人の人数と子どもの人数を確認する。
⇒大人6人、子ども3人
②公式に当てはめて計算する。
大人の人数×4+子どもの人数×2-3
6×4+3×2-3=24+6-3
=27(回)
よって、正解は3番の選択肢(27回)になります。
必勝法
例題1
太郎さんと花子さんがドングリを使って、次のようなルールでゲームを行う。
・ドングリは、50個ある。
・ドングリを最小で1個、最大で5個ずつ交互に取っていく。
・最後の50個目を取ることになった者が負けとする。
太郎さんが先攻のとき、太郎さんが花子さんに必ず勝つために、最初に取らなければならないドングリの個数として、最も妥当なものはどれか。
- 1. 1個
- 2. 2個
- 3. 3個
- 4. 4個
- 5. 5個
必勝法とは
必勝法とは、〇個の対象物(どんぐりやコインなど)を2人で交互に取っていき、最後の1つを取った者が負けor勝ちというゲームをします。1度に取れる個数は問題によって異なります。(1~5個までなど)
先攻の者が必ず勝つために、最初に取る対象物の個数を求める問題です。
本来の解き方
50個目を取った方が負けになるので、先攻である太郎さんは49個めを取り交代すれば勝つことになる。お互い1個~5個を取れるので、相手が何個取ろうと、2人が取る個数の合計を6個にすることができる(相手が4個取ったら自分は2個など)。ここから、49個目を必ず取るためには、43個目を取ればよい。同様に、43個目を取るためには、37個目を取ればよく、37個目を取るには31個目を取ればよい。このように考えると、先攻である太郎さんは初めに1個とれば、7個目、13個目、19個目、25個目、31個目、37個目、43個目、49個目を取ることができ、必ず勝つことができる。
必勝法の解き方
(個数-1)÷(最小+最大)の余り
この余りの数を先攻が取れば必ず勝てる!
例題1の解説・解答
今回は50個目のどんぐりを取ると負けてしまいます。そのため、
(50-1)÷(1+5)=49÷6
=8あまり1
先攻の太郎さんが最初に1個取れば勝ち!
よって選択肢1の1個が正解になります。
例題2
A、Bの2人で交互にコインを取り続け、最後のコインを取った人が負けとなるゲームをしている。コインは全部で39枚であり、1人が一度に1枚以上4枚以下のコインを取り、AもBも勝つための最善を尽くすとする。Bが先手のときに、確実にいえるのはどれか。
- 1. Bは最初に1枚とれば、必ず勝てる。
- 2. Bは最初に2枚とれば、必ず勝てる。
- 3. Bは最初に3枚とれば、必ず勝てる。
- 4. Bの取る枚数に関わらず、先手のBは必ず勝てる。
- 5. Bの取る枚数に関わらず、後手のAは必ず勝てる。
例題2の解説・解答
今回は39枚目のコインを取ると負けてしまい、1人が1度に取れるコインは、最小1枚、最大4枚です。
(個数-1)÷(最小+最大)の余り
この余りの数を先攻が取れば必ず勝てる!
この公式を使って、
(39-1)÷(1+4)=38÷5
=7あまり3
先攻のBが最初に3枚取れば勝ち!
よって選択肢3が正解となります。
油分け算
例題1
水が満たされている容量10Lの容器と、容量7L及び容量3Lの空の容器がそれぞれ1つずつある。3つの容器の間で水を順次移し替え、容量10Lの容器と容量7Lの容器とへ、水をちょうど5Lずつに分けた。各容器は容量分の水しか量れず、1つの容器から別の1つの容器へ水を移し替えることを1回と数えるとき、 水をちょうど5Lずつに分けるのに必要な移し替えの最小の回数として、正しいのはどれか。
- 1.8回
- 2.9回
- 3.10回
- 4.11回
- 5.12回
本来の解き方
① 大→中→小→大…と順番に移す
② 以前に同じ作業を行っている場合はその作業を飛ばす
| 大(10L) | 中(7L) | 小(3L) | |
|---|---|---|---|
| 最初 | 10 | 0 | 0 |
| ① | 3 | 7 | 0 |
| ② | 3 | 4 | 3 |
| ③ | 6 | 4 | 0 |
| ④ | 6 | 1 | 3 |
| ⑤ | 9 | 1 | 0 |
| ⑥ | 9 | 0 | 1 |
| ⑦ | 2 | 7 | 1 |
| ⑧ | 2 | 5 | 3 |
| ⑨ | 5 | 5 | 0 |
やり方を説明します。
1回目は大→中に移すため、大に入っていた10Lのうち7Lを中に移します。そうすると大は3L残ります。これを次は中→小と繰り返していきます。

ここで④に注目してください。
4回目は大→中ですが、大→中に移すと(大)3(中)7(小)0となってしまい、①と同じになってしまいます。そのため、大→中の作業を飛ばし、4回目は中→小の作業を行います。
その後は同様に繰り返していきます。
その結果、9回で5Lずつを作ることができるので、選択肢2が正解となります。
油分け算の解き方
② 「ずつ」があるかないかに注目
③ ある場合とない場合にわけて考える
・ずつが「ある」場合⇒「①の合計-1」が答え
・ずつが「ない」場合⇒「①の合計-2」が答え
【参考】
| 中 | 小 | 作る量 | 「ずつ」 | 回数 |
|---|---|---|---|---|
| 5 | 3 | 4 | × | 6回 |
| 5 | 3 | 4 | 〇 | 7回 |
| 7 | 3 | 5 | × | 8回 |
| 7 | 3 | 5 | 〇 | 9回 |
| 8 | 3 | 4 | × | 10回 |
| 7 | 5 | 6 | × | 10回 |
| 7 | 5 | 6 | 〇 | 11回 |
| 9 | 7 | 8 | × | 14回 |
| 9 | 7 | 8 | 〇 | 15回 |
| 11 | 7 | 9 | × | 16回 |
| 11 | 7 | 9 | 〇 | 17回 |
例題1の解説・解答
今回の問題では、(中)7L(小)3Lで、「ずつ」があるため、
7+3-1=9回ということになります。
例題2
7Lと9Lの空の容器と水の入った大きな水槽がある。これらの容器を使って水をくんだり移し替えたりする操作を繰り返し、9Lの容器に8Lの水を入れるためには、最低何回の操作が必要か。ただし、1回の操作とは、次のア~ウのうちいずれか一つだけであるものとする。
ア どちらか一方の容器で、大きな水槽から水をくむ。
イ どちらか一方の容器から、他方の容器に水を移し替える。
ウ どちらか一方の容器から、大きな水槽に水を移し替える。
- 1.14回
- 2.15回
- 3.16回
- 4.17回
- 5.18回
例題2の解説・解答
② 「ずつ」があるかないかに注目
③ ある場合とない場合にわけて考える
・ずつが「ある」場合⇒「①の合計-1」が答え
・ずつが「ない」場合⇒「①の合計-2」が答え
今回の問題では、(大)は水槽であるため、(中)が9L(小)7Lとなります。
また、「ずつ」はないので、
9+7-2=14回
よって選択肢1が正解になります。
天秤
例題1
見た目は全く同じコインが50枚ある。この中に1枚だけ他より軽いコインが混ざっていて、残りの49枚は同じ重さである。1台の天秤ばかりを使って、確実に軽いコインを見つけるための最少の回数として、最も妥当なものはどれか。ただし、偶然に見つけた回数は最少とはしないものとする。
- 1.3回
- 2.4回
- 3.5回
- 4.6回
- 5.7回
天秤の問題とは
見た目が全く同じもの(コインや重り)の中から天秤だけを使って、1つだけ重さが違うものを見つけるための天秤の最小使用回数を求める問題です。
天秤問題の解き方
1枚だけ他より軽い(重い)ものを見つける場合の天秤の使用回数は、
全部の枚数が
4~9枚⇒2回
10~27枚⇒3回
28~81枚⇒4回
82~243枚⇒5回
例題1の解説・解答
今回の問題はコインの枚数が50枚ですので4回
よって選択肢2が正解になります。
例題2
100枚の金貨があり、この中に1枚だけ本物より軽いニセ金貨が混じっている。ニセ金貨以外の99枚はすべて同じ重さであるとき、確実にニセ金貨を見つけるために天秤ばかりを使う採用の回数はどれか。ただし、偶然に見つけた回数は最少としない。
- 1.3回
- 2.4回
- 3.5回
- 4.6回
- 5.7回
例題2の解説・解答
今回、金貨の枚数は100枚です。
天秤の使用回数は、全部の枚数が
4~9枚⇒2回
10~27枚⇒3回
28~81枚⇒4回
82~243枚⇒5回
100枚は82~243枚の間ですので、天秤の使用回数は5回ということになります。
よって選択肢3が正解になります。
嘘つき①
例題1
A、B、C、D、Eの5人のグループがおり、この5人のうち誰がリーダーなのかを各人に尋ねたところ以下のように返答した。本当のことを言っている者は1人だけで残りの4人は嘘をついていることがわかっているとき、本当のことを言っているのは誰か。
A「CとEはリーダーではない」
B「AとDはリーダーではない」
C「DかEのどちらかだ」
D「BかCのどちらかだ」
E「AとBはリーダーではない」
- 1.A
- 2.B
- 3.C
- 4.D
- 5.E
嘘つき問題①の解き方
噓つき問題①は、表を使って嘘つきを見つける問題です。
② 〇(×)の数の合計を出す
③ 表をタテに見て選択肢を検討する
例題1の解説・解答
① 発言を表に整理します。
発言をタテ、リーダーをヨコとし、発言を整理します。
Aは、「CとEはリーダーではない」と発言している。この発言から、「リーダーは、AかBかDの誰かである」ということが読み取れます。
そのため、表のAの発言、A・B・Dの部分に〇を入れます。
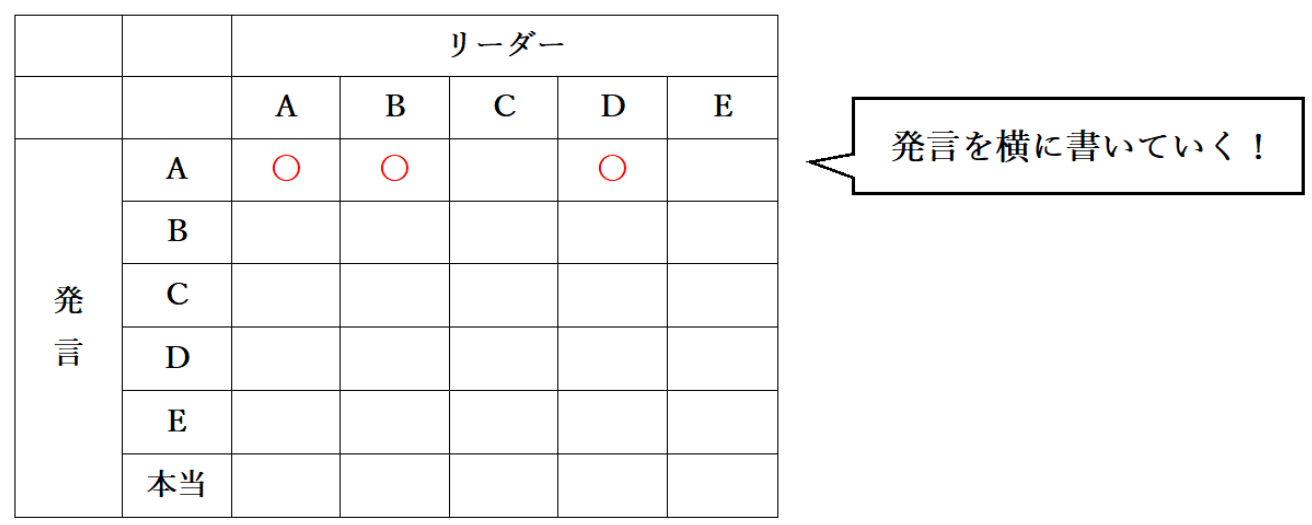
② B、C、D、Eの発言も同様に表に埋めていき、〇の数を数えます。
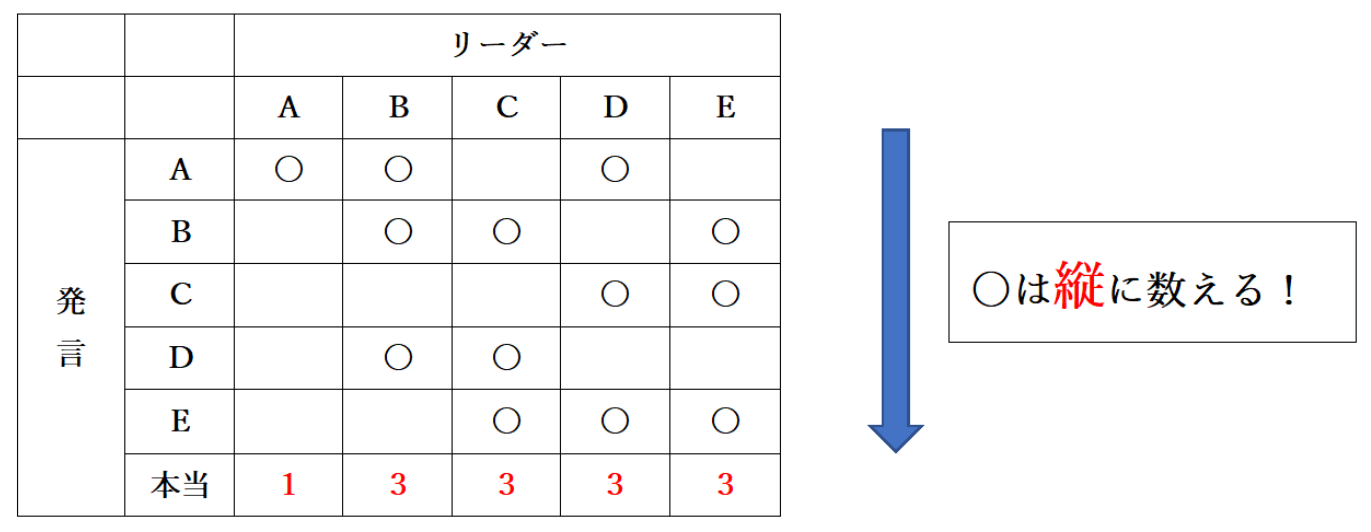
③ 表をタテに見て選択肢を検討していきます。
この表は人ごとに縦に見ます。
例えば、仮にリーダーがBのとき、本当のことを言っている者はA、B、Dの3人ということになります。
今回の問題では、本当のことを言っている者は1人なのでリーダーはAになります。
よって選択肢1が正解になります。
例題2
A~Eの5人がある検定試験を受け、このうちの1人が合格した。5人に試験の結果を聞いたところ、次のような返事が返ってきた。このとき、本当のことを言っているのが1人のみだとすると、確実に言えるものはどれか。
A「合格はDでも私でもない。」
B「合格はCかEのどちらかである。」
C「合格はAでもBでもない。」
D「合格はAか私のどちらかである。」
E「合格はBでも私でもない。」
- 1. Aは、本当のことを言っている。
- 2. Bは、本当のことを言っている。
- 3. Cは、本当のことを言っている。
- 4. Dは、本当のことを言っている。
- 5. Eは、本当のことを言っている。
例題2の解説・解答
① 発言を表に整理します。
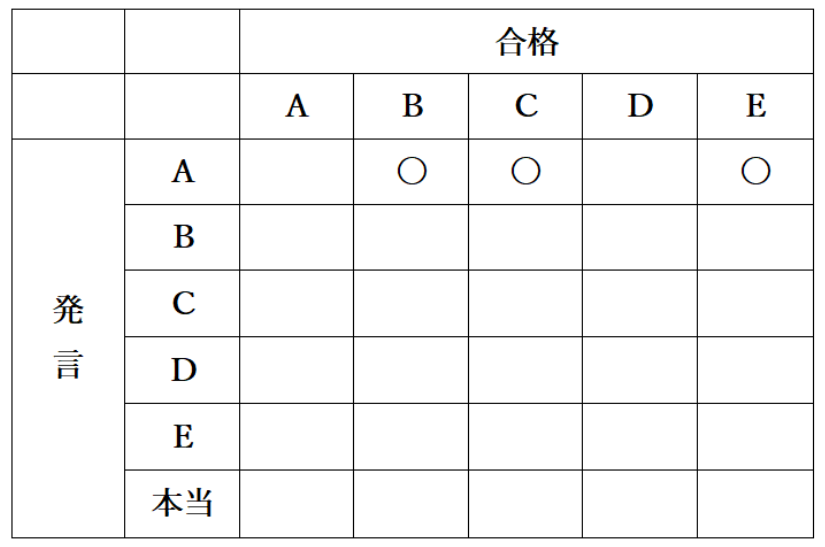
発言をタテ、合格をヨコとし、発言を整理します。
Aは、「合格はDでも私でもない」と発言しています。この発言から、「合格は、BかCかEの誰かである」ということが読み取れます。
そのため、表のAの発言、B・C・Eの部分に〇を入れます。
発言は横に書いていきます!
② B、C、D、Eの発言も同様に表に埋めていき、〇の数を数えます。
〇の数は縦に数えます!
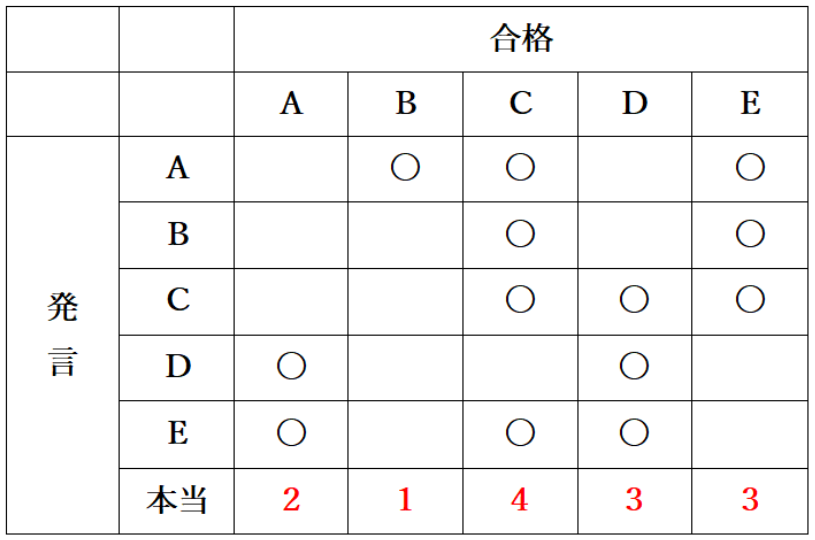
③ 表をタテに見て選択肢を検討していきます。
この表は人ごとに縦に見ます。
例えば、仮に合格者がAのとき、本当のことを言っている者はDとEの2人ということになります。
今回の問題では、本当のことを言っている者は1人なので合格者はBになります。よってBが合格だと言っているAが本当のことを言っている人ということになります。
よって選択肢1が正解になります。
噓つき②
例題1
A~Eの5人が次のように述べているとき、確実に言えるものはどれか。ただし、5人は正直者またはうそつきのいずれかであり、うそつきは発言中の下線部分が虚偽であるものとする。
A:「Bはうそつきである。」
B:「Cはうそつきである。」
C:「Dはうそつきである。」
D:「Eはうそつきである。」
E:「AとBは2人ともうそつきである。」
- 1. Aは正直者である。
- 2. Dは正直者である。
- 3. Eは正直者である。
- 4. うそつきは2人である。
嘘つき問題②の解き方
噓つき問題②では、グループに分けて考えます。
① A「Bはうそつき」⇒AとBは別グループ
② A「Bは正直者」⇒AとBは同じグループ
例題1の解説・解答
① A「Bはうそつき」⇒AとBは別グループ
② A「Bは正直者」⇒AとBは同じグループ
まずポイントに当てはめA~Dの発言について整理します。
Aの発言より、AとBは別グループ。
Bの発言より、BとCは別グループ。
Cの発言より、CとDは別グループ。
Dの発言より、DとEは別グループ。
ということが分かります。
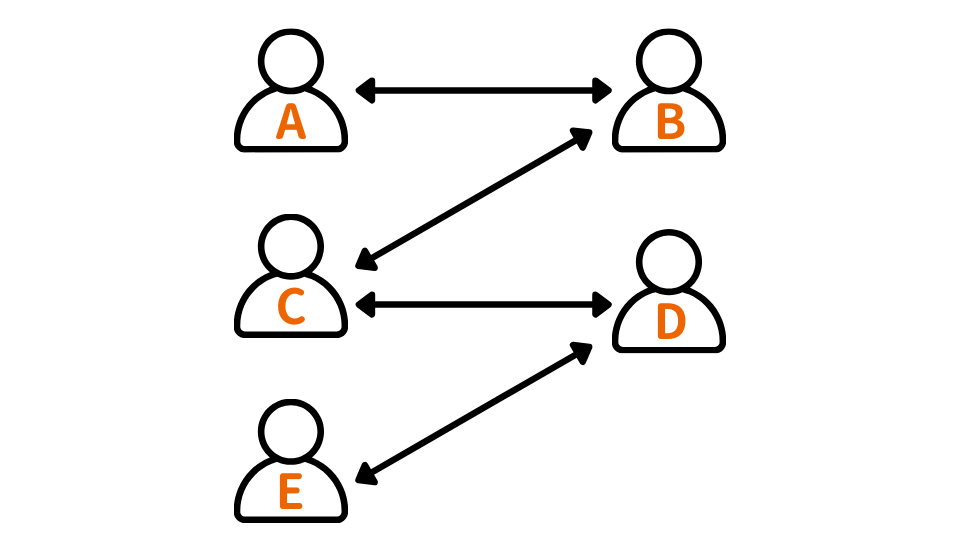
A~Dの発言より、
ACEのグループとBDのグループに分けられ、どちらかがうそつきのグループ、どちらかが正直者のグループということになります。
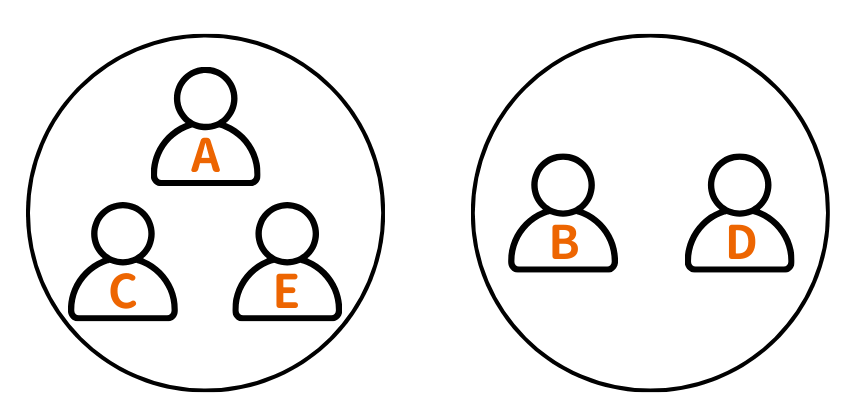
最後にEの発言を検討します。
Eは「AとBは2人ともうそつきである。」といっており、グループ分けの結果からあり得ないため、Eはうそつきということになります。
そのため、ACEがうそつきのグループ、DBが正直者のグループということになります。
よって選択肢2が正解になります。
例題2
A~Dが次のように言っている。この4人のうち、少なくとも2人が正しいことを言っているとき、正しいことを言っている者のみをすべて挙げているのはどれか。
A:「Bの言っていることは常に正しい。」
B:「Cの言っていることは常に正しくない。」
C:「Dの言っていることは常に正しくない。」
D:「Aの言っていることは常に正しい。」
- 1. A、B、C
- 2. A、B、D
- 3. A、D
- 4. B、C
- 5. C、D
例題2の解説・解答
まず、A~Dの発言を整理します。
Aは「Bの言っていることは常に正しい」と言っています。これはつまり「Bは正直者だ」と言い換えることが出来ます。Bの発言の同様に、「Cの言っていることは常に正しくない」を「Cはうそつきだ」と言い換えることが出来ます。
このことを踏まえて発言を整理すると、
Aの発言より、AとBは同じグループ。
Bの発言より、BとCは別グループ。
Cの発言より、CとDは別グループ。
Dの発言より、DとAは同じグループ。
ということが分かります。
発言をまとめると、ABDのグループとCのグループに分けられます。
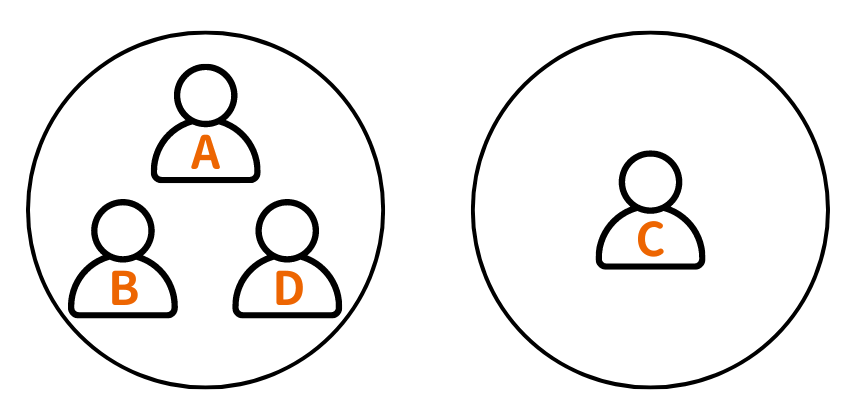
今回の問題では、少なくとも2人が正しいことを言っているため、ABDのグループが正直者のグループ、Cがうそつきのグループということになります。
よって選択肢2が正解になります。
集合の最少人数
例題1
ある会社の社員40人について、嫌いな野菜を調べたところ次のことが分かった。
A セロリが嫌いな社員は32人であった。
B ゴーヤが嫌いな社員は29人であった。
C ケールが嫌いな社員は26人であった。
以上から判断して、セロリ、ゴーヤ及びケール全てが嫌いな社員は少なくとも何人いるか。
- 1.6人
- 2.7人
- 3.8人
- 4.9人
- 5.10人
集合の最少人数とは
集合の最少人数とは、ある団体の中で~な人は少なくとも何人いるのかを求める問題です。
本来の解き方
社員40人のうち、セロリが嫌いな社員が32人います。ここから、40人中残り8人はセロリが嫌いではいことがわかります。この8人全員が、ゴーヤが嫌いだったと仮定して考えます。
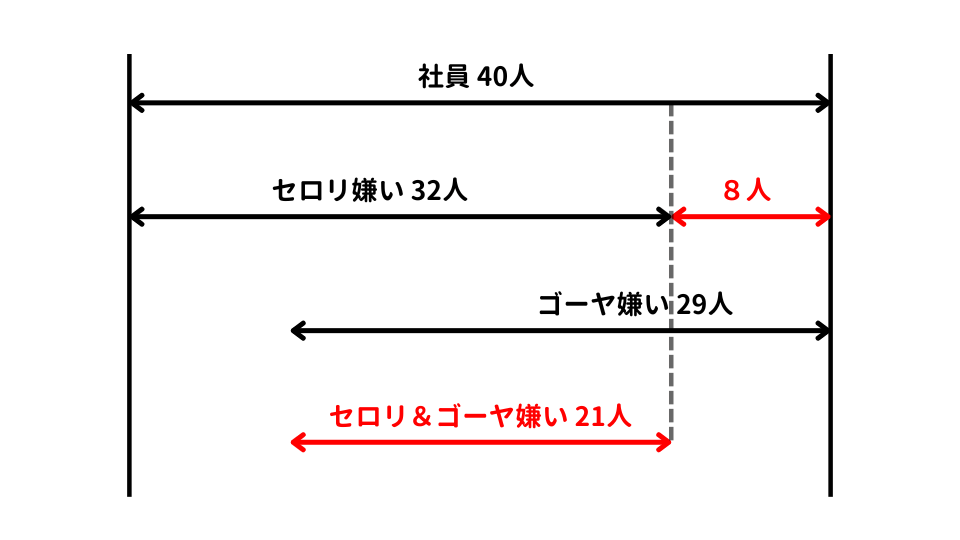
どれだけ少なく見ても、セロリとゴーヤの両方が嫌いな社員は29-8=21人いることになります。
同様に、40人中、セロリとゴーヤの両方が嫌いな社員が21人おり、そうではない社員が19人いることがわかります。この19人全員が、ケールが嫌いだったと仮定して考えます。
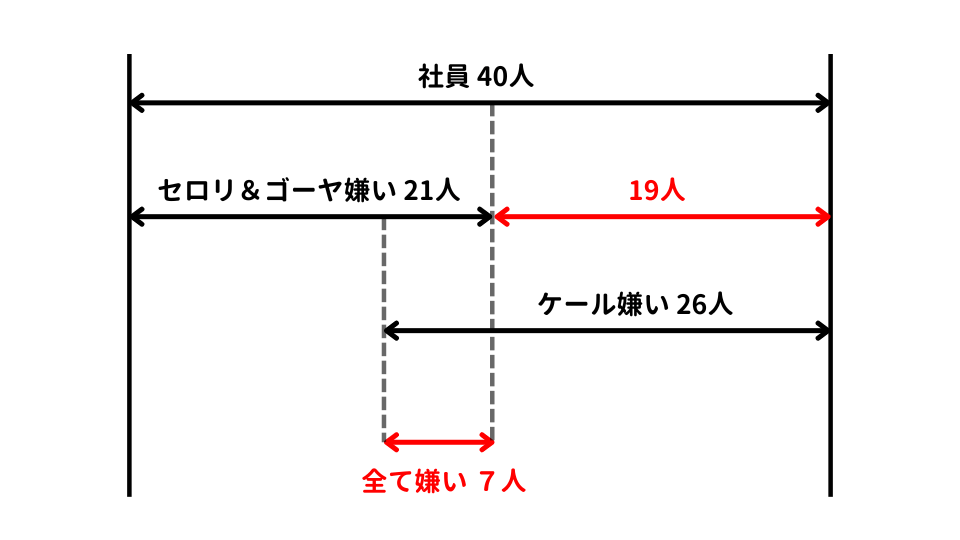
どれだけ少なく見ても、3つの野菜全てが嫌いな社員は26-19=7人ということになります。
したがって、選択肢2が正解となります。
集合の最少人数の求め方
例題1の解説・解答
この公式の意味を解説すると、「それぞれの人数の合計」=「セロリ」「ゴーヤ」「ケール」が嫌いな社員の合計ということになります。また、全体の人数は社員の人数=40人、質問の個数はA~Cの3つであるため、(質問の個数-1)=(3-1)=2ということになります。
よって以下の公式に当てはめると、
それぞれの(嫌いな)人数の合計-全体の人数×2
32+29+26-40×2=87-80
=7(人)
例題2
40人のクラスメイトに好きな科目のアンケートを実施したところ、英語が好きな者が36人、数学が好きな者が34人、国語が好きな者が30人いることがわかった。このとき、英語と数学と国語の3科目とも好きな者の最少人数として、最も妥当なのはどれか。ただし、すべての科目が好きではない者はいなかったものとする。
- 1.12人
- 2.15人
- 3.20人
- 4.24人
- 5.28人
例題2の解説・解答
今回の問題では、
それぞれの人数の合計=英語と数学と国語が好きな人数の合計なので、
英語が好きな36人
+数学が好きな34人
+国語が好きな30人
=100
全体の人数=40人
質問の個数-1=3(英語、数学、国語)-1=2
したがって、36+34+30-40×2=100-80
=20(人)
よって選択肢3が正解になります。
例題3
一人暮らしの大学生50人を対象に、家具・家電製品の所持状況に関する調査を実施したところ、以下のことが分かっているとき、ベッド、コタツ、アイロン、パソコン全てを所持している学生の最少人数として、最も妥当なものはどれか。
・ベッドを所持している者:37人
・コタツを所持している者:32人
・アイロンを所持している者:41人
・パソコンを所持している者:45人
- 1.5人
- 2.6人
- 3.7人
- 4.8人
- 5.9人
例題3の解説・解答
今回の問題も以下の公式を利用することが出来ます。
それぞれの人数の合計-全体の人数×(質問の個数-1)
それぞれの(所持)人数の合計=ベッド、コタツ、アイロン、パソコンを所持している学生の人数の合計
全体の人数=50人
質問の個数-1=4(ベッド、コタツ、アイロン、パソコン)-1=3
以上を公式に当てはめると、
37+32+41+45-50×3=155-150
=5(人)
よって選択肢1が正解になります。
ハノイの塔
例題1
A~Cの3本の棒が板の上に立てられており、Aの棒には中央に穴の開いた大きさの異なる3枚の円盤が下から大きい順に積み重ねられている。次のア、イのルールに従って、この3枚の円盤を全てCの棒に移すには、最低何回の移動が必要か。
ア 円盤は1回に1枚だけ他の2本の棒のいずれかに移し替えることとする。
イ 小さい円盤の上に大きい円盤を重ねることはできない。
- 1.5回
- 2.6回
- 3.7回
- 4.8回
- 5.11回
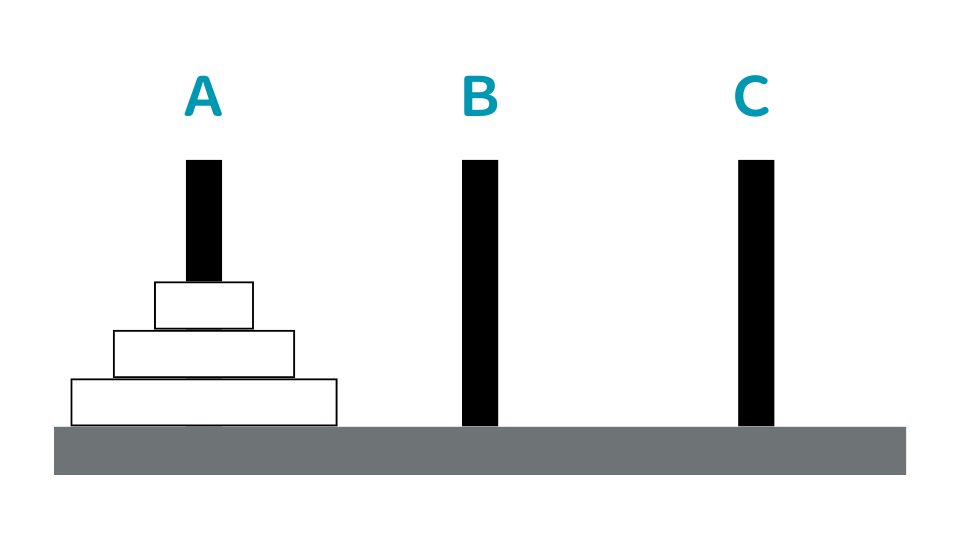
本来の解き方
① AからCに小を移動させます。
② AからBに中を移動させます。
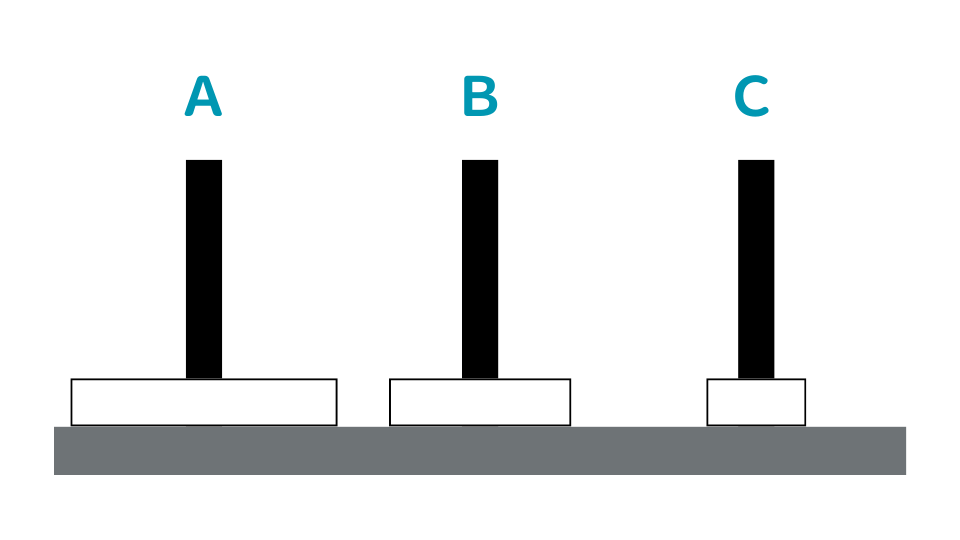
③ イの条件より、CからBに小を移動させます。
④ AからCに大を移動させます。
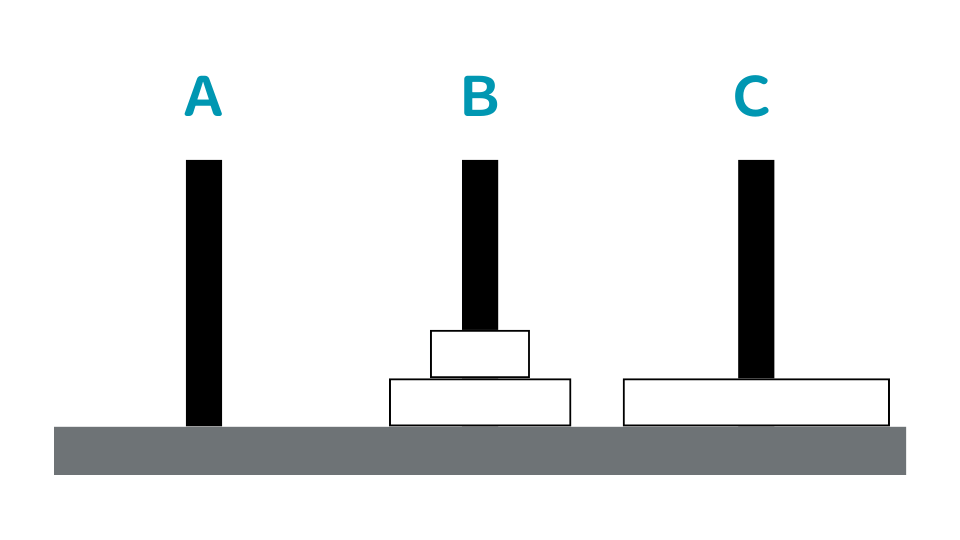
⑤ BからAに小を移動させます。
⑥ BからCに中を移動させます。
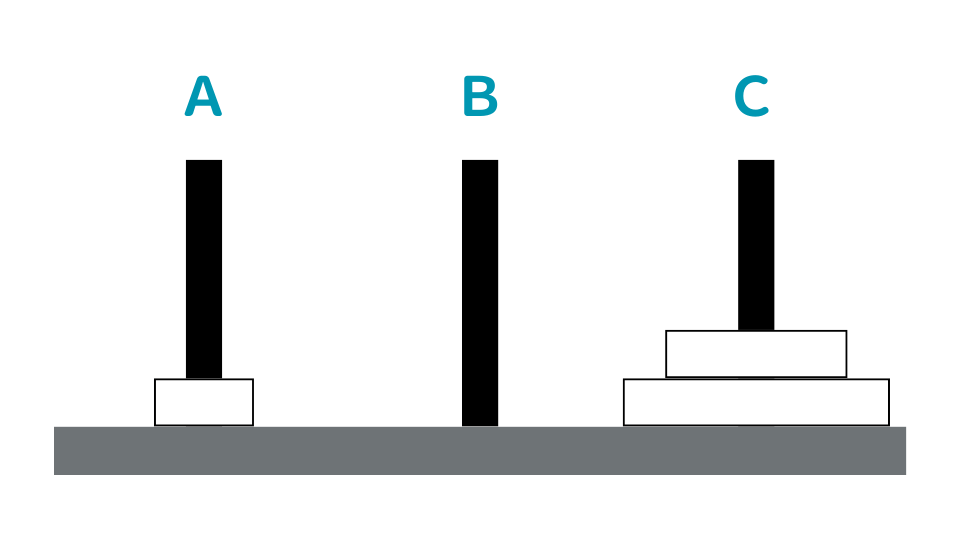
⑦ AからCに小を移動させます。
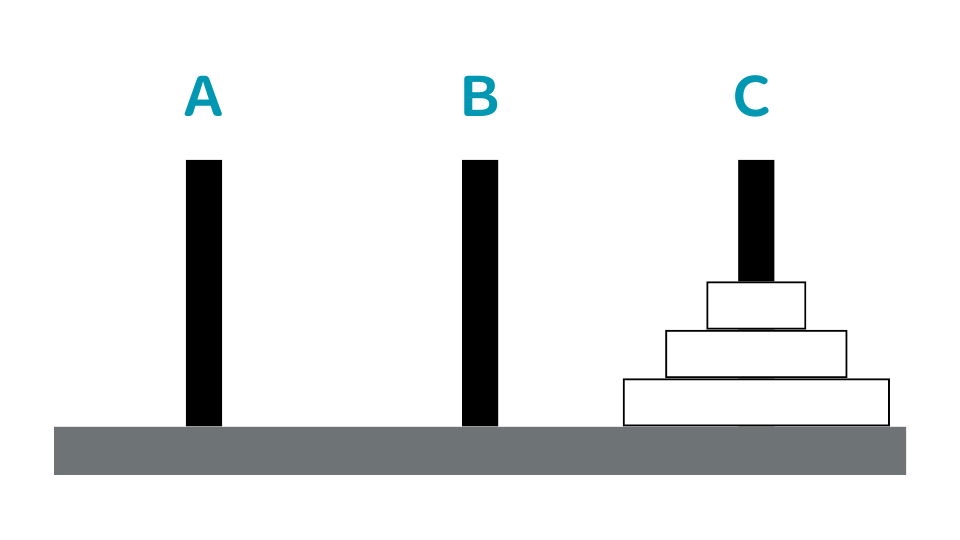
7回移動させると3枚の円盤を全てCの棒に移すことができます。
よって選択肢3が正解になります
ハノイの塔の解き方
2ⁿ―1
例題1の解説・解答
今回の問題では、3枚の円盤を移動させるので、
2³-1=8-1
=7(回)
例題2
次の図のように、A~Cの3本の容器がある。Aの容器には、Ⅰ~Ⅳの数字が書かれた4個のボールが下から数字の大きい順に入っており、BとCの容器は空である。Aの容器の4個のボールをCの容器に図のように移すには、最低何回の移動が必要か。ただし、ボールは1個の移動につき1個ずつ他の容器に動かし、小さい数字の上に大きい数字のボールをのせないものとする。
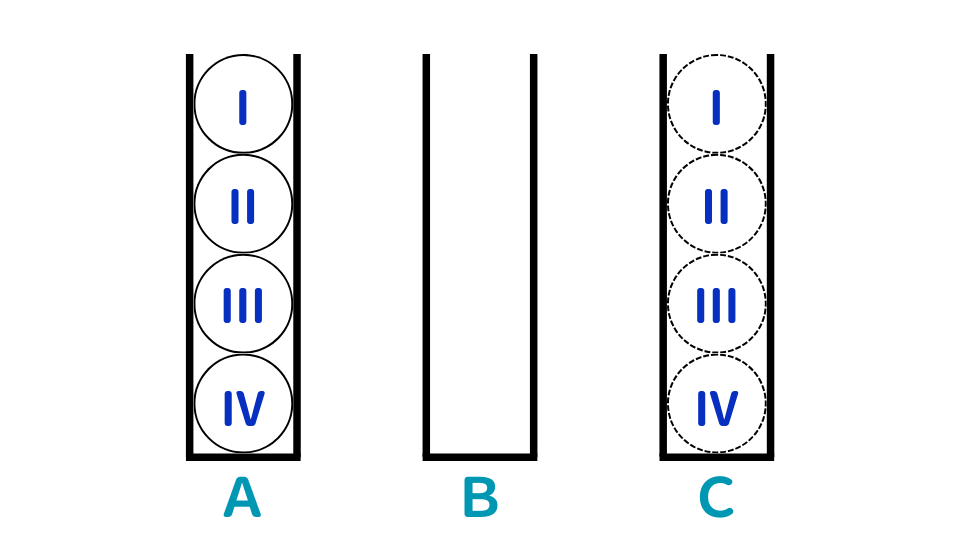
- 1.7回
- 2.9回
- 3.11回
- 4.13回
- 5.15回
例題2の解説・解答
今回の問題も数字の大きさが異なるボールを1個ずつ移動させるため、ハノイの塔の問題と考えることが出来ます。
2ⁿ―1
上記の公式を使い、今回は4つのボールを移動させるため、
2⁴ -1=16-1
=15(回)
よって選択肢5が正解になります。
正八面体の展開図
例題1
下の展開図を組み立てて正八面体を作ったとき、面Aと平行になる面として、最も妥当なものはどれか。
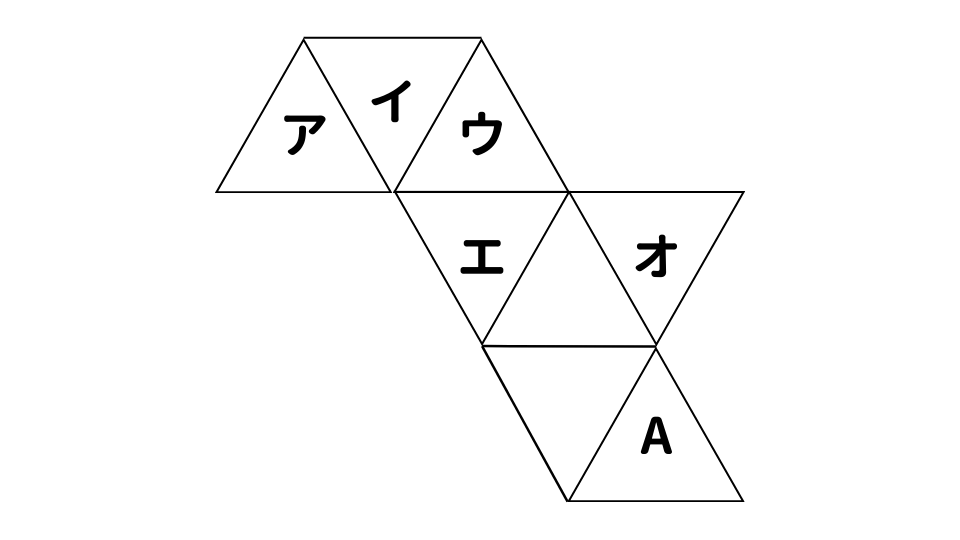
- 1.ア
- 2.イ
- 3.ウ
- 4.エ
- 5.オ
正八面体の展開図とは
正八面体の展開図とは組み立てたときに、ある面と平行になる面はどれかを求める問題です。
まず、正八面体とはどのような立体なのか見てみましょう。
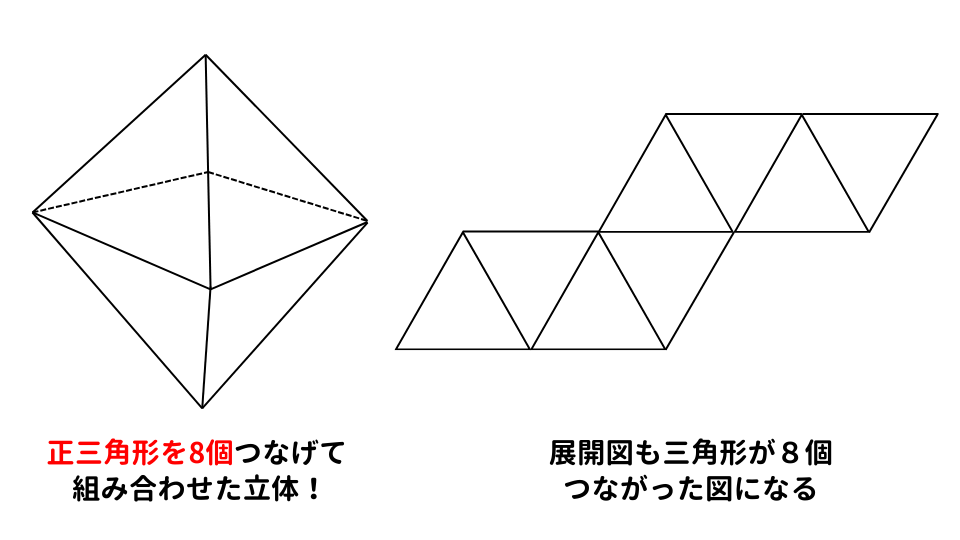
正八面体の展開図の解き方
直線で3つとなり(2個とばし)が平行となる。
例題1の解説・解答
今回の問題では、面Aと平行の面を求めるため、
面Aから直線で2個とばしの面エが向かい合う面ということになります。
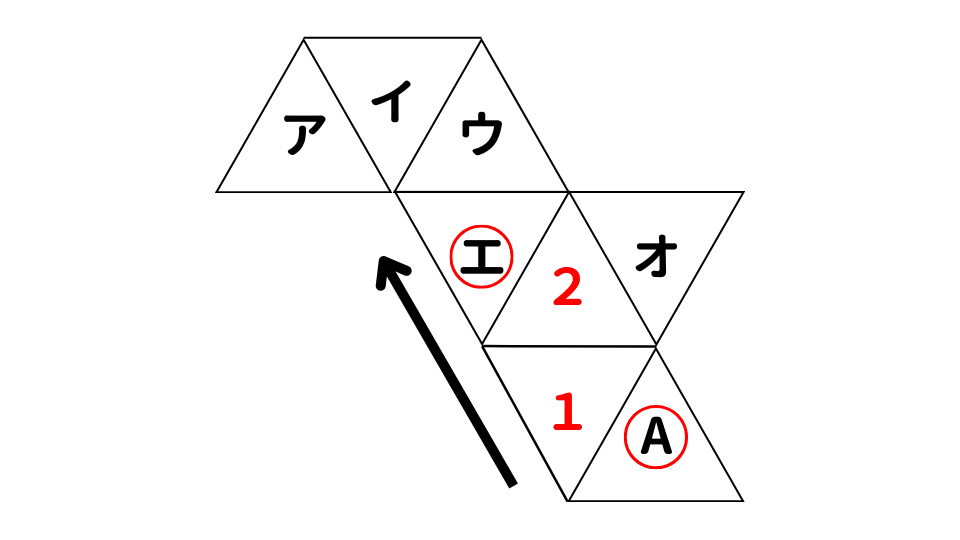
直線で2個とばしであるため、面オではなく面エとなります。
よって選択肢4が正解となります。
例題2
図は各面に書かれた正八面体の展開図である。これを組み立てた正八面体について、平行に向かい合う面の数字が合計して10になる面の組み合わせは何組あるか。
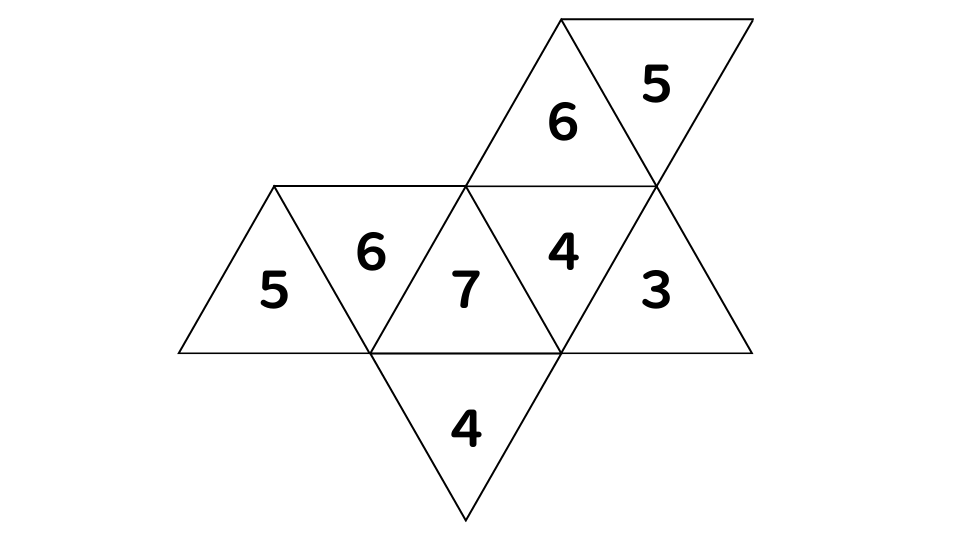
- 1.0組
- 2.1組
- 3.2組
- 4.3組
- 5.4組
例題2の解説・解答
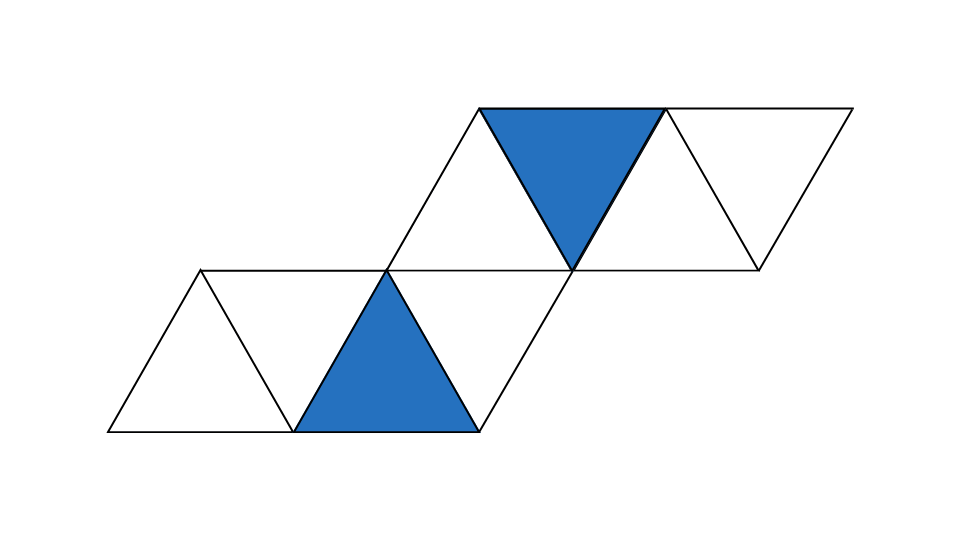
まず、平行に向かい合う面はどことどこなのかを確認していきます。
正八面体の展開図を組み立てたとき、平行になる面は、ある面の3つとなり(2個とばし)となります。
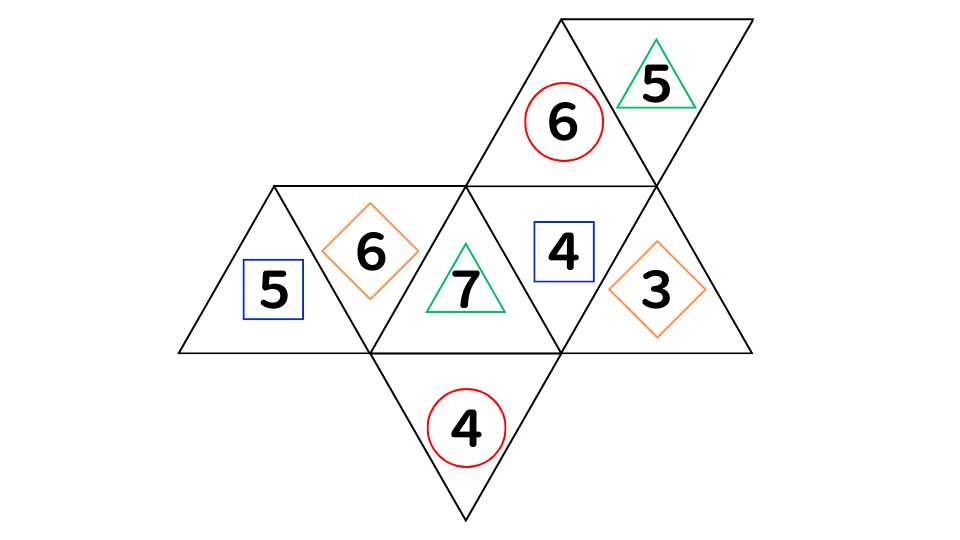
※マークが同じ面が平行になります!
平行になる面を確認すると、合計して10になるのは〇の1組だけということが分かります。
よって選択肢2が正解となります。
円の分割
例題1
下図は円内の平面に3本の直線を引き、円内の平面を分割したところを表している。この円内に5本の直線を書き加えることによって分割される平面の最大の数として、最も妥当なものはどれか。
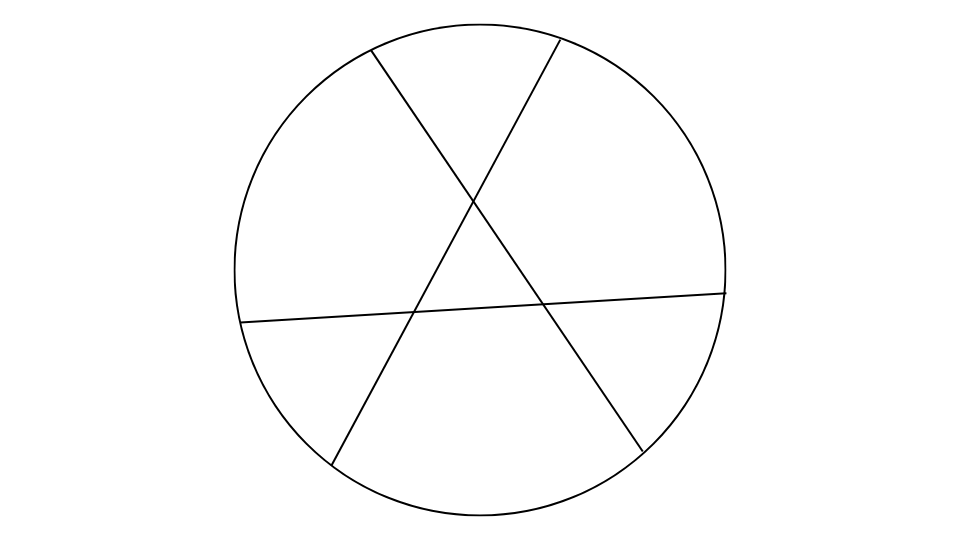
- 1. 34
- 2. 35
- 3. 36
- 4. 37
- 5. 38
円の分割とは
円の分割とは、〇本の線で円を分割したら最大いくつの平面ができるか?という問題です。
円の分割の解き方
例題1の場合、赤線を3本足すと円は18個に分割されます。
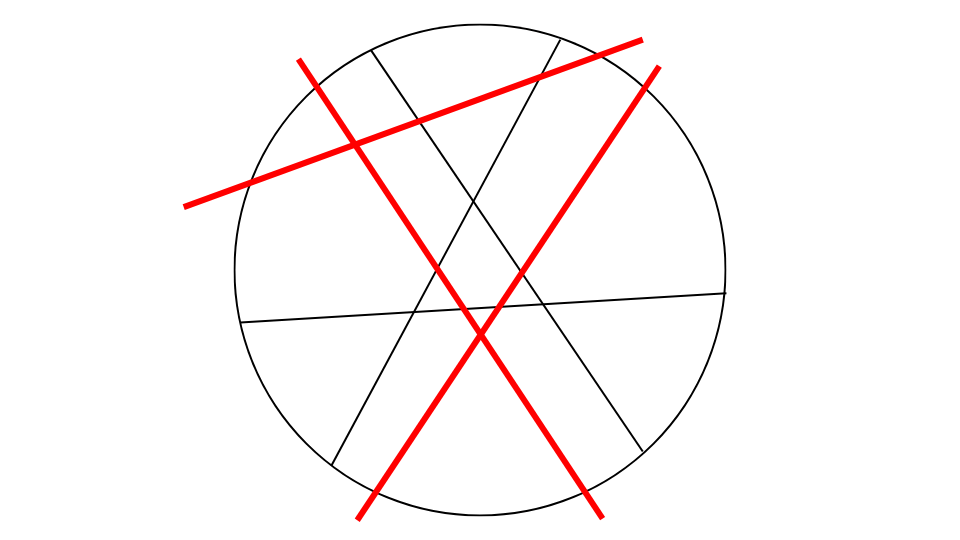
しかし、1本でも線を引き間違えてしまうと分割される数が異なってしまいます。
そのため、線を引いて解くのは不可能!
そこで解き方のポイント!
⇒1~〇本の合計+1
例題1の解説・解答
現在、3本の線が引いてあり、円は7か所に分かれています。
ここから更に5本の線を引いて最大何個に分けることができるのかを求めます。
今回は、合計8本の線を引くので、
1 + 2 + 3 + 4 +5+ 6 + 7 + 8 +1=37
よって正解の選択肢は4になります。
例題2
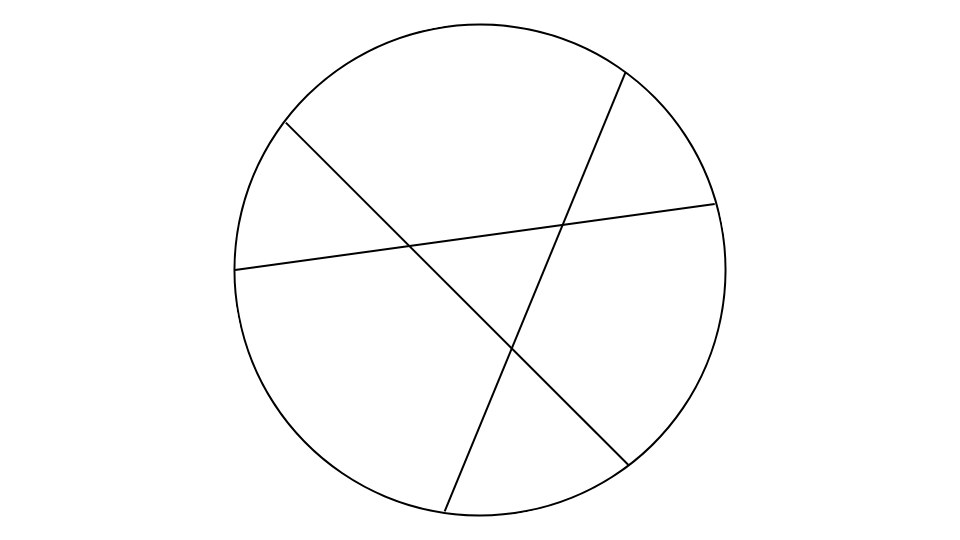
次の図のように3本の直線によって分割された円がある。
今、7本の直線を加えてこの円を分割したとき、分割されてできた平面の最大数はどれか。
- 1. 56
- 2. 57
- 3. 58
- 4. 59
- 5. 60
例題2の解説・解答
今回はすでに3本の線が引いてあり、ここに7本の線を加えるため、
3+7=10で合計10本の線を引きます。
⇒1~〇本の合計+1
先ほどの公式に当てはめると、
1 + 2 + 3 + 4 +5+ 6 + 7 + 8 +9+ 10 +1=56
よって正解の選択肢は1になります。
LINE公式にご登録頂くと、自動的に「裏技・テクニックまとめ」が送付されます。
[/box]
数的推理
時計算
例題1
アナログ時計が6時ちょうどを示した後、長針と短針が最初に重なるのは何分後か。
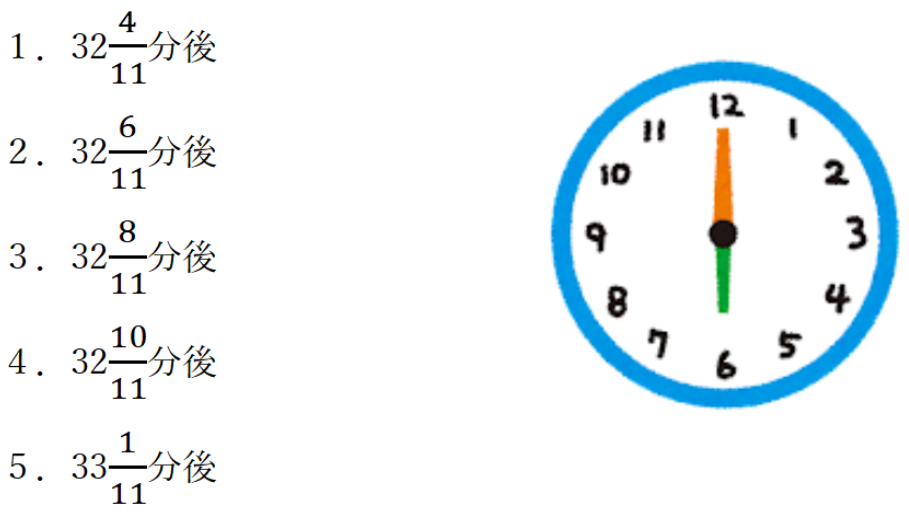
時計算とは
時計算とは、〇時になった後に長針と短針が重なるのは何分後かを求める問題です。
本来の解き方
〇時の長針と短針の間:〇×30度
例えば、3時だったら長針と短針の間は3×30度=90度となります。

時計の長針:1時間(60分)で1周(360度)動く⇒1分で6度動く
時計の短針:12時間(720分)で1周(360度)動く⇒1分で0.5度動く
よって長針と短針の間⇒1分で5.5度縮まります。
今回の問題は6時であるため、長針と短針の間は6×30=180°開いています。
また、長針と短針の間は1分間で5.5度縮まるため、
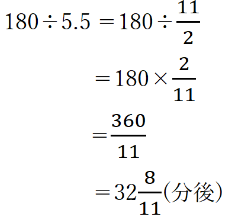
よって選択肢3が正解になります。
時計算の解き方
② 足して一の位が0になるものが答え
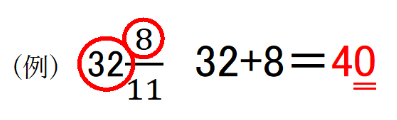
例題1の解説・解答
① 選択肢を見て、帯分数の整数と分子の数を足し算します。
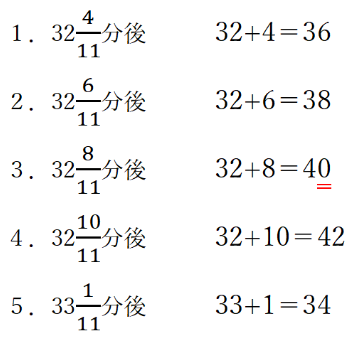
② 一の位が0になっている 選択肢3が正解になります。
例題2
下の図のような時計があり、7時30分を指している。この時計で7時30分から8時のあいだに、長針と短針がちょうど重なる時刻として、最も妥当なのはどれか。ただし、長針と短針はそれぞれ一定の速さで動いているものとする。
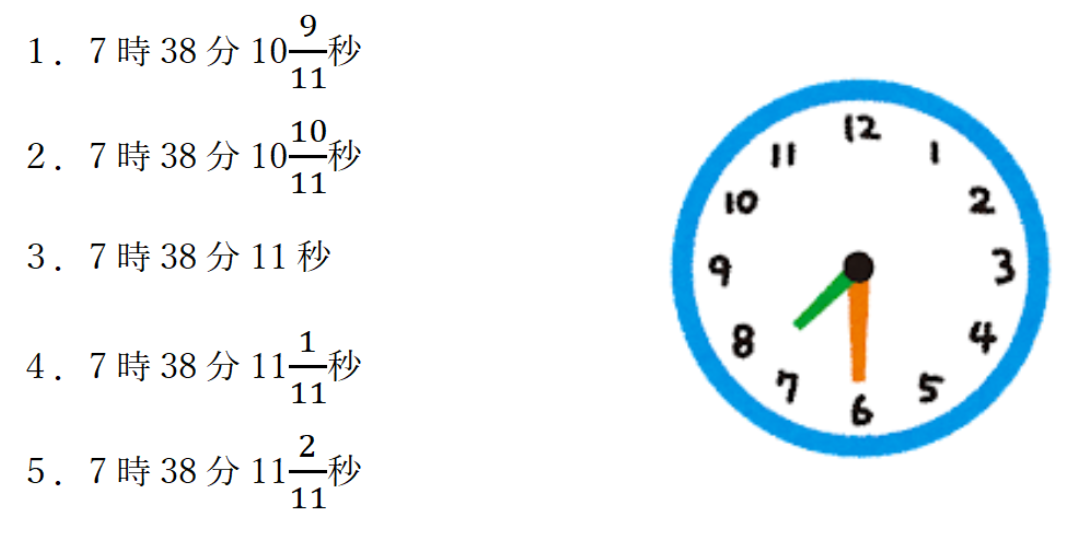
例題2の解説・解答
② 足して一の位が0になるものが答え
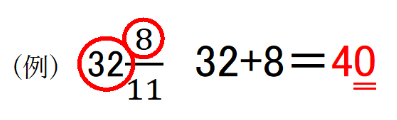
今回の問題では、
1. 10+9=19 ×
2. 10+10=20 〇
3. 11 ×
4. 11+1=12 ×
5. 11+2=12 ×
よって選択肢2が正解となります。
例題3
アナログ時計では、3時00分に長針と短針のなす角が90°になる。次に時計の長針と短針のなす角が90°になるのは何分後か。
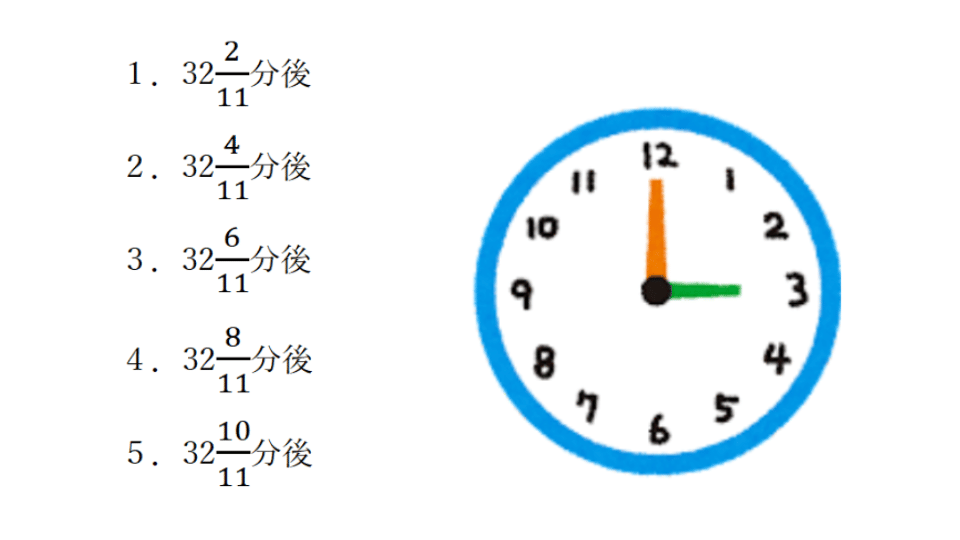
例題3の解説・解答
今回の問題は、長針と短針が重なる問題ではありませんが、公式を使って一瞬で解くことが出来ます。
1. 32+2=34 ×
2. 32+4=36 ×
3. 32+6=38 ×
4. 32+8=40 〇
5. 32+10=42 ×
よって選択肢4が正解となります。
道順
例題1
A地点からB地点まで行くが次の図のようになっているとき、A地点からB地点まで行く道順は何通りか?ただし、最短経路で行くものとする。
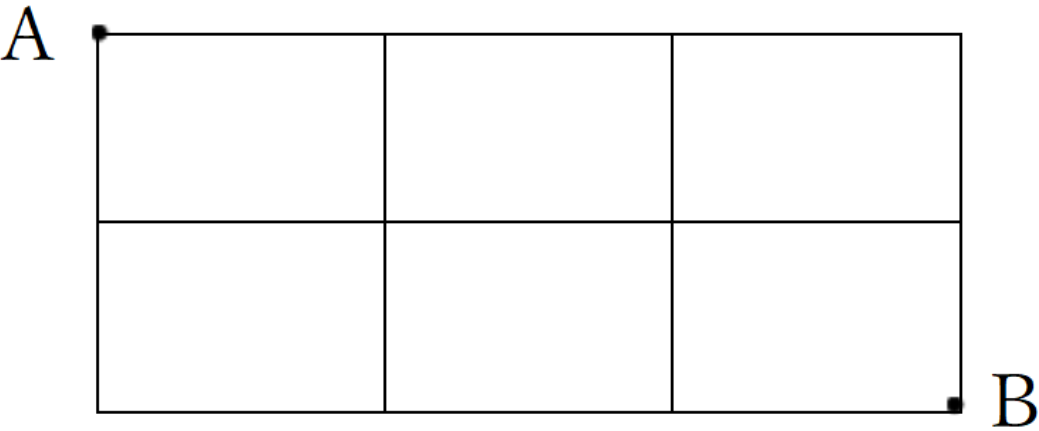
道順の解き方
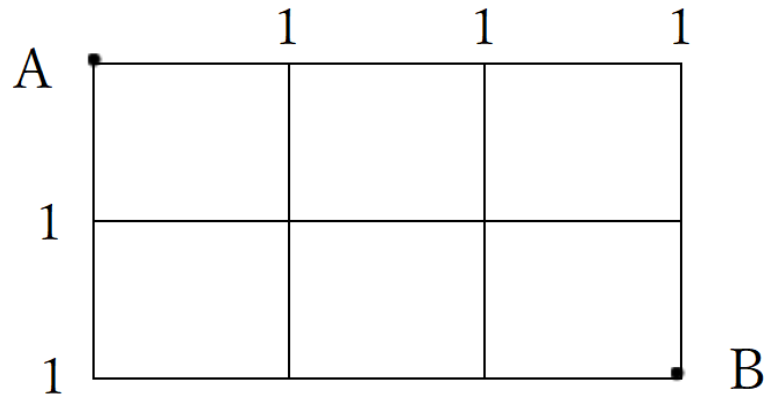
② 残りの交差点は上と右の数字をたすだけ!
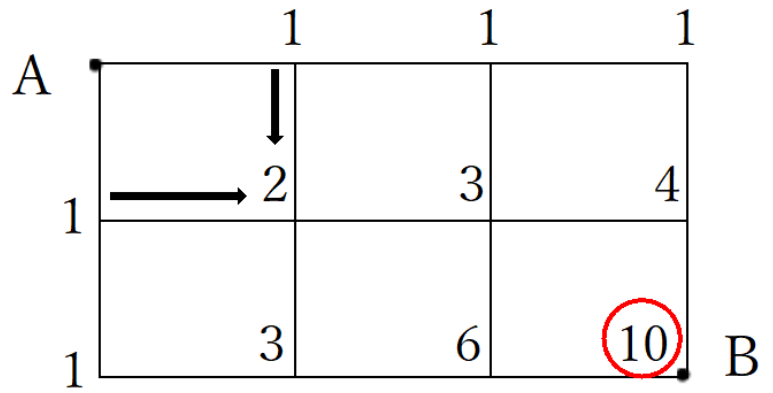
よってBまでは10通りになります。
例題2
A地点からB地点まで行くが次の図のようになっているとき、A地点からB地点まで行く道順は何通りか?ただし、最短経路で行くものとする。
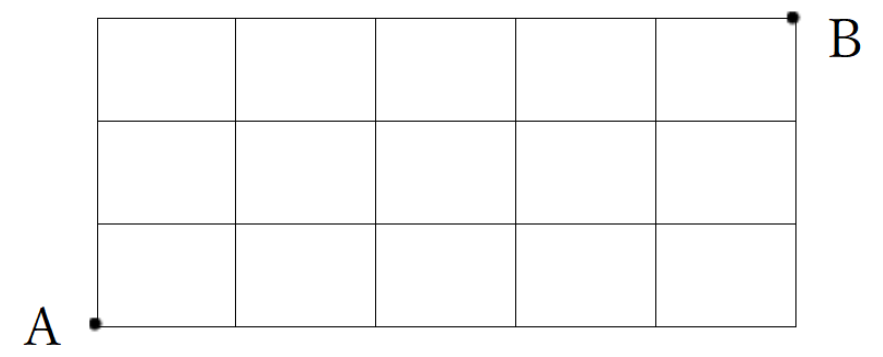
例題2の解説・解答
① スタート(A)の上と右の交差点に1と書く
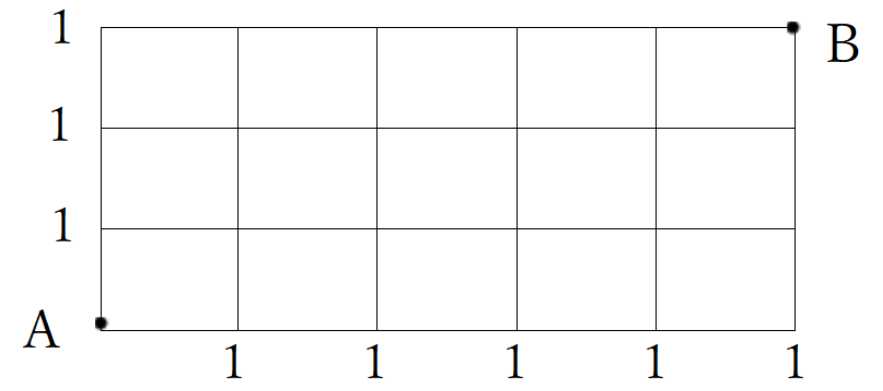
② 残りの交差点は下と左の数字をたすだけ!
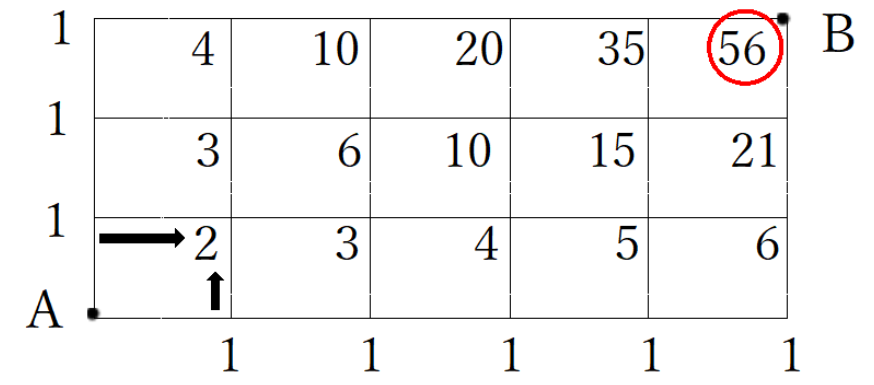
よってBまでは56通りになります。
例題3
下の図のような碁盤目状の街路網において、AからBを通ってCまで最短経路行く道順は何通りか?
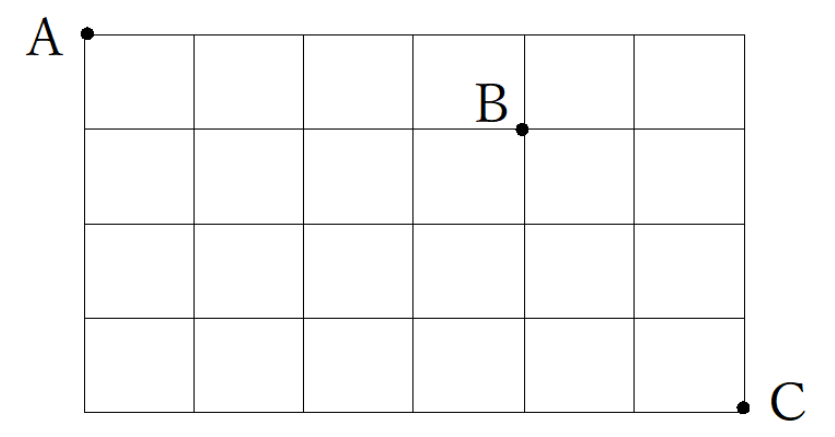
例題3の解説・解答
例題3のように、必ず通らなければならない場所がある場合は次のように求めます。
① Bまで何通りか求める
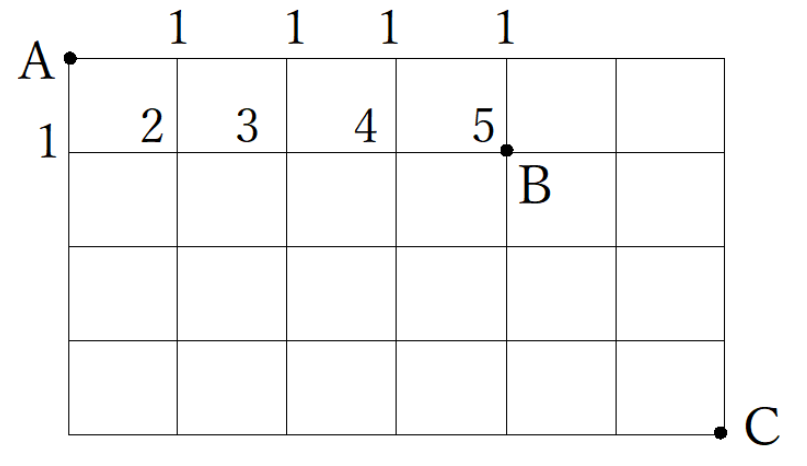
② Bまでが5通りなので、Bから下と右の交差点に5と書く
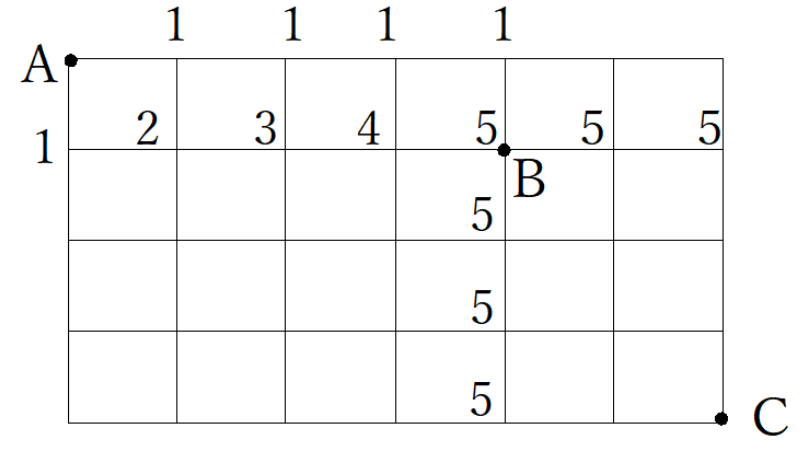
③ 残りの交差点は上と左の数字をたす
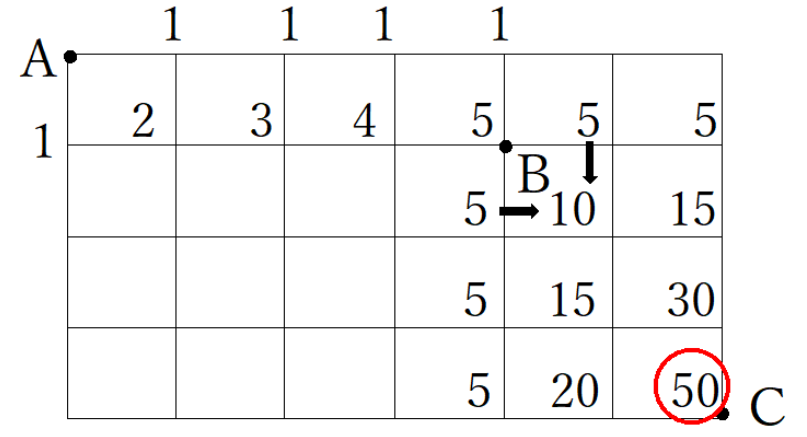
よってCまでは50通りになります。
例題4
下の図において、線上をたどってA点からB点へ行くときの最短経路は何通りか?
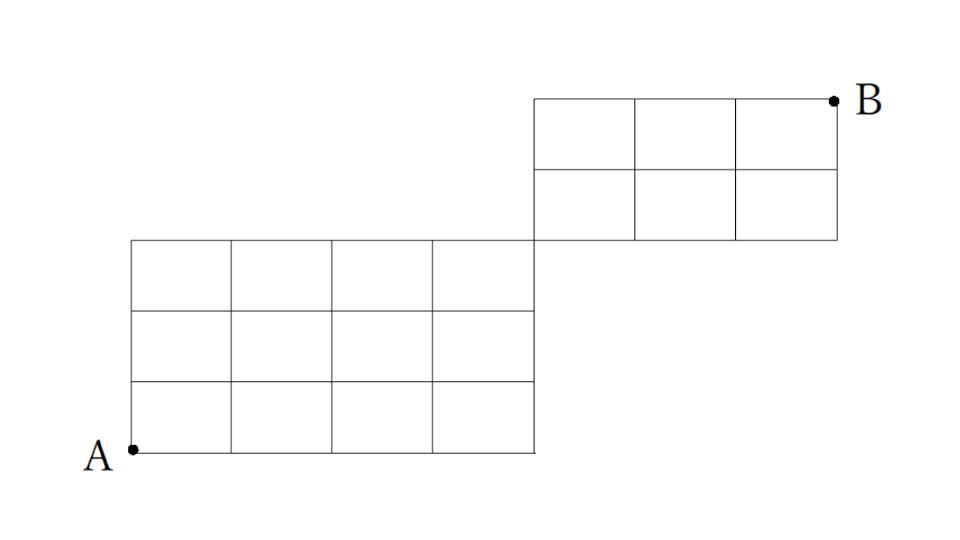
例題4の解説・解答
① 中間地点をC点とし、C点まで何通りあるかを求める。
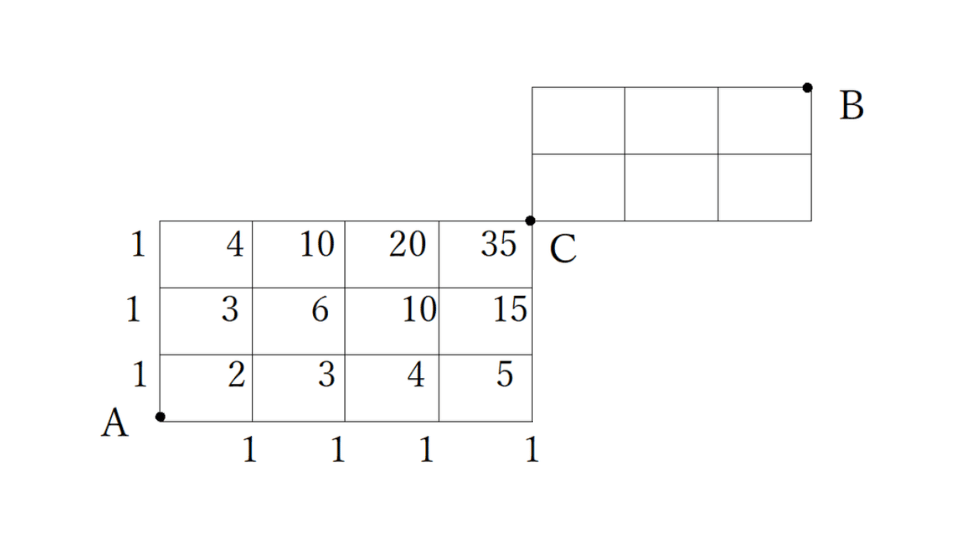
② Cまでが35通りなので、Cから上と右の交差点に35と書く
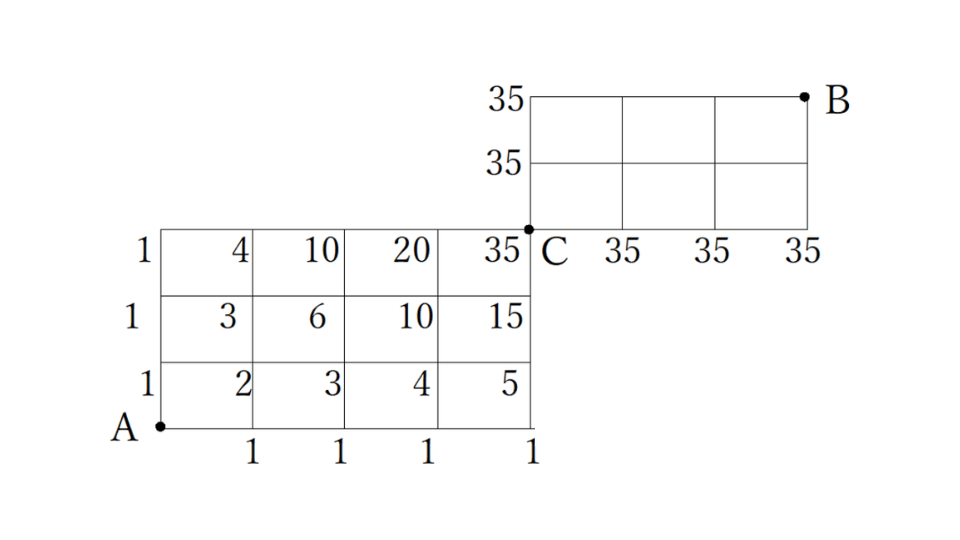
③ 残りの交差点は下と左の数字をたす
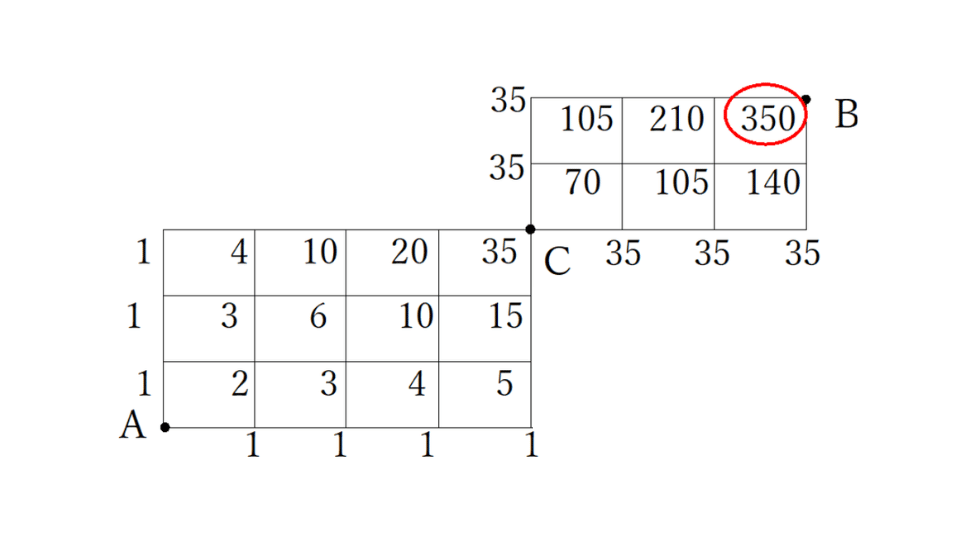
よってBまでは350通りになります。
例題5
下図のような街路において、A点及びB点を最短距離で結ぶ経路は全部で何通りなるか。

- 1. 50通り
- 2. 51通り
- 3. 52通り
- 4. 53通り
- 5. 54通り
例題5の解説・解答
例題5のように道がない部分がある場合、次のようにして解く。
①線を加える
道がない部分に線を加え、そこに0と書く。
そして、Aの上と右の交差点部分に1と書く。
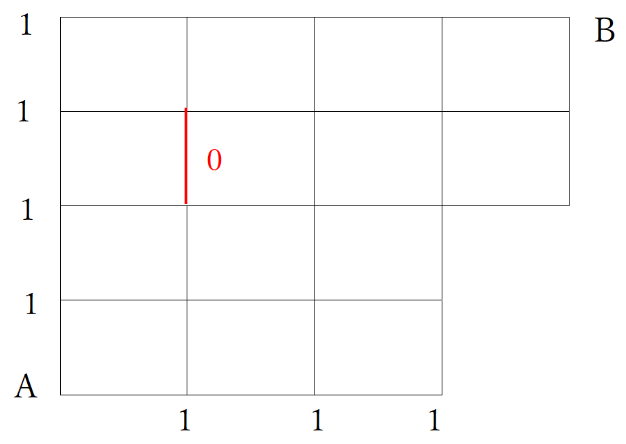
② 左とすぐ下の数字の合計を交差点に書く。
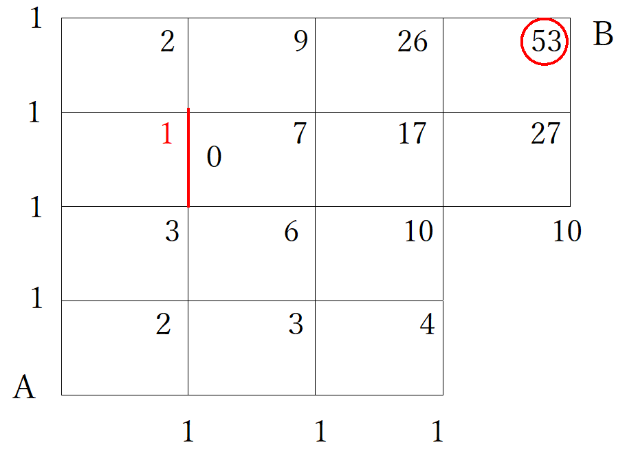
Iの部分
ここは左の1と下の0をたして1+0=1となります。
このとき、Bで53となるため、53通りとなります。
よって選択肢4が正解となります。
LINE公式にご登録頂くと、自動的に「裏技・テクニックまとめ」が送付されます。
[/box]
図形・空間把握
切断面の面積
例題1
次の図のような、1辺の長さが10㎝の立方体がある。辺ABの中点をP、辺DEの中点をQとして、この立方体を点C、P、Qを通る平面で切断したとき、その断面の面積はどれか。
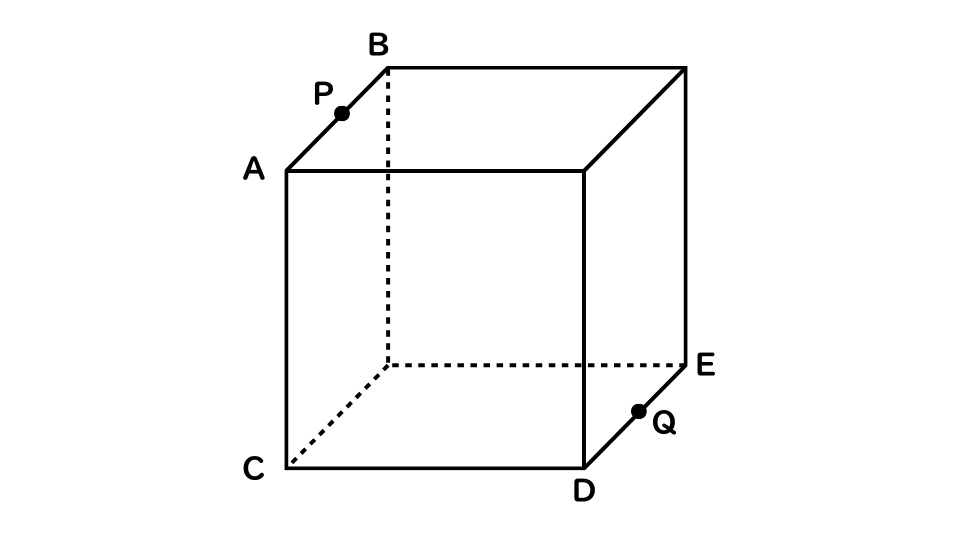
- 1.25√2㎠
- 2.25√6㎠
- 3.50√2㎠
- 4.50√6㎠
- 5.125㎠
切断面の面積とは
切断面の面積とは、立体を切断したときの切断面の面積を求める問題です。
本来の解き方
① 切断面を書く。
切断面は「ひし形」になる
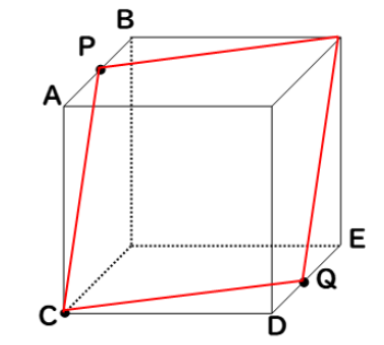
② 対角線の長さを求める
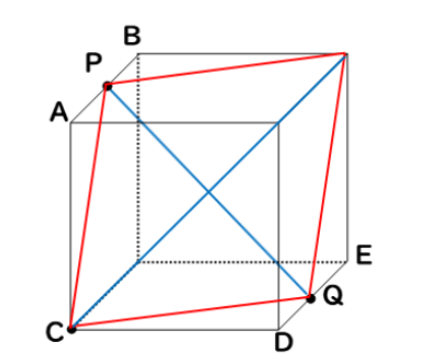
ひし形の面積=対角線×対角線÷2
切断面の面積の求め方
本来の解き方のように、「断面図を書いて、対角線の長さを求めて...」 と考えるのは時間もかかるし大変。 そこで解き方のポイント!
1辺×1辺×√6÷2
例題1の解説・解答
1辺×1辺×√6÷2
この問題の1辺の長さは10㎝であるので、
10×10×√6÷2
=100√6÷2
=50√6
よって選択肢4が正解になります。
例題2
次の図のような、1辺4㎝の立方体がある。この立方体を点A、B、Cを通る平面で切断したとき、その断面の面積はどれか。
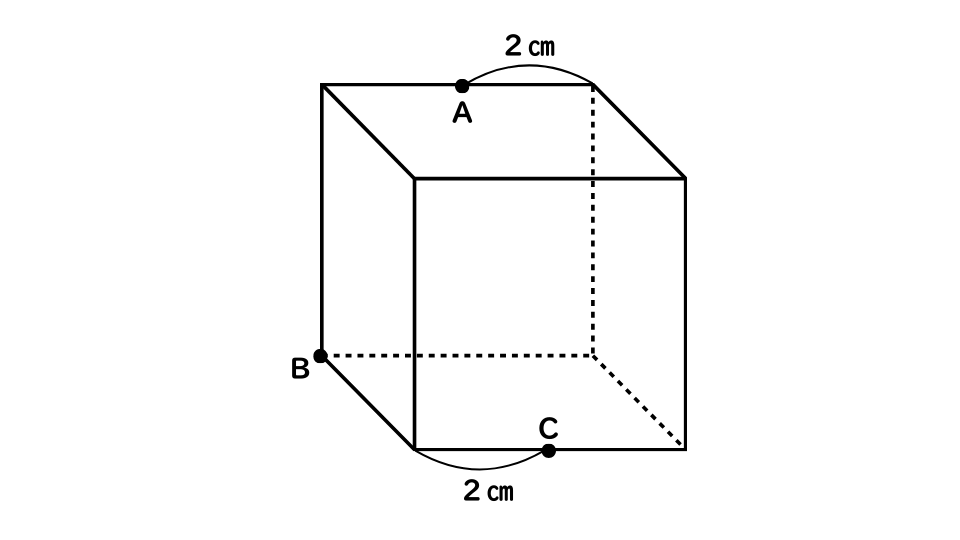
- 1.4√6㎠
- 2.4√15㎠
- 3.8√5㎠
- 4.8√6㎠
- 5.20㎠
例題2の解説・解答
AとCが中点でBが角となっているため、公式を使うことが出来ます。
1辺×1辺×√6÷2
今回の問題では、1辺の長さが4cmであるため、
4×4×√6÷2
=16√6÷2
=8√6
よって選択肢4が正解になります。
角度の総和
例題1
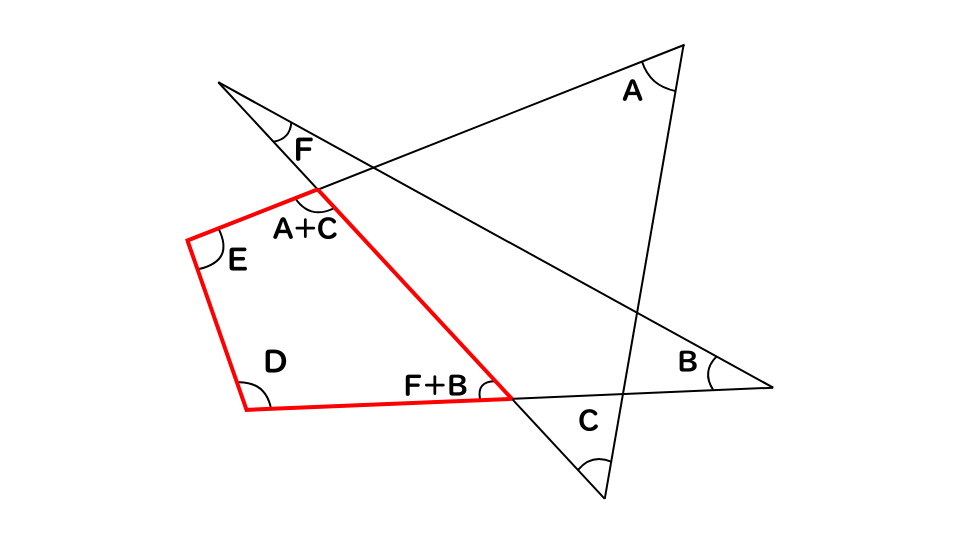
次の図において、角度A~Fの和はどれか。
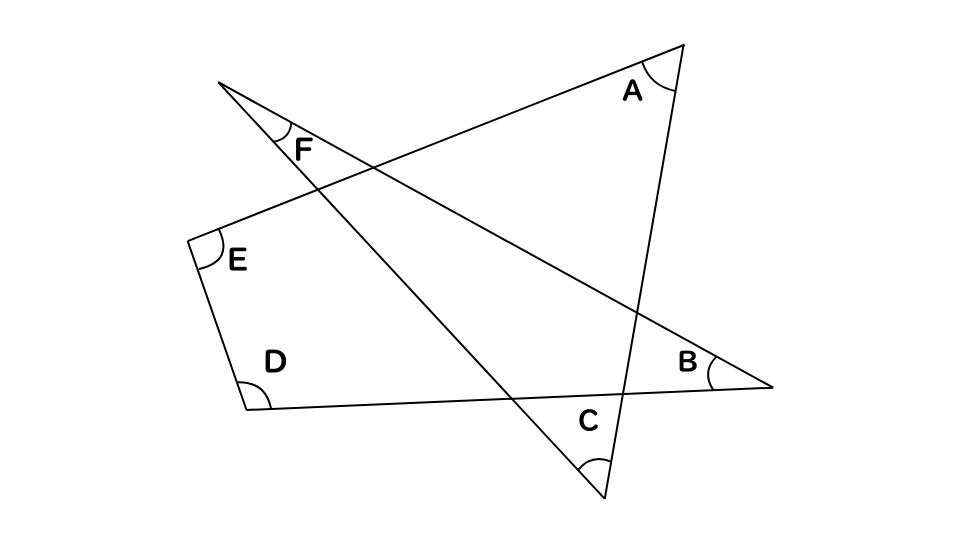
- 1.300°
- 2.360°
- 3.420°
- 4.480°
- 5.540°
角度の総和とは
角度の総和とは、多角形の角度の総和を求める問題です。
本来の解き方
本来は三角形の外角を利用して解きます。
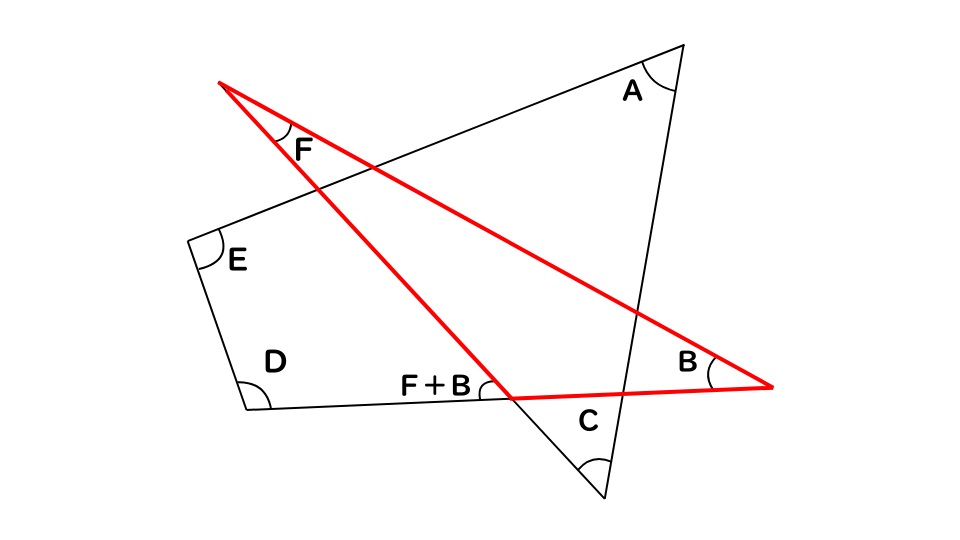
三角形の2つの角の合計(F+B)は残り1つの角の外角と等しい!
同様に、A+Cの値も出すことが出来ます。
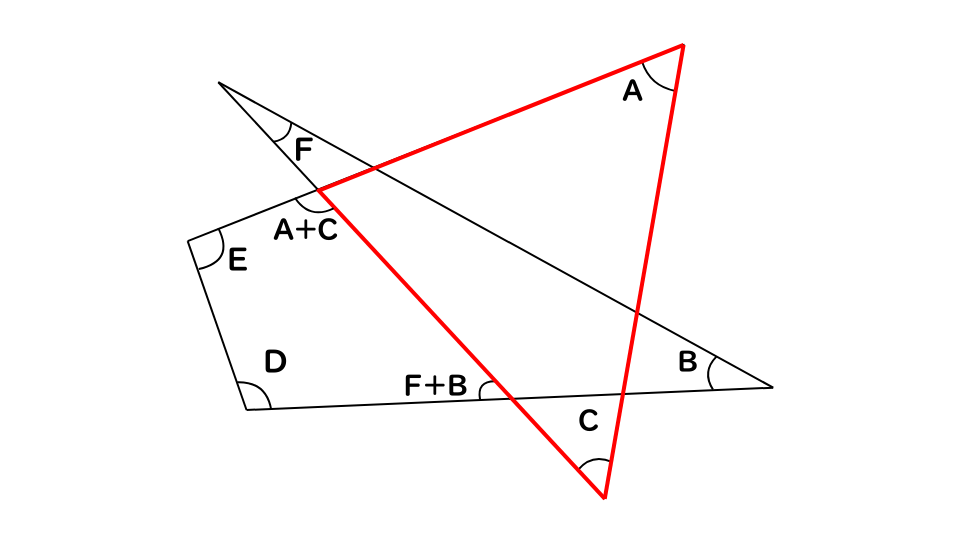
すると、1つの四角形にA~Fの角が集まり、四角形の内角の和は360°なので、角の和は360°となります。
角度の総和の求め方
例題1の解説・解答
今回の問題では、角が6個なので、
(6-4)×180°
=2×180°
=360°
よって選択肢2が正解となります。
例題2
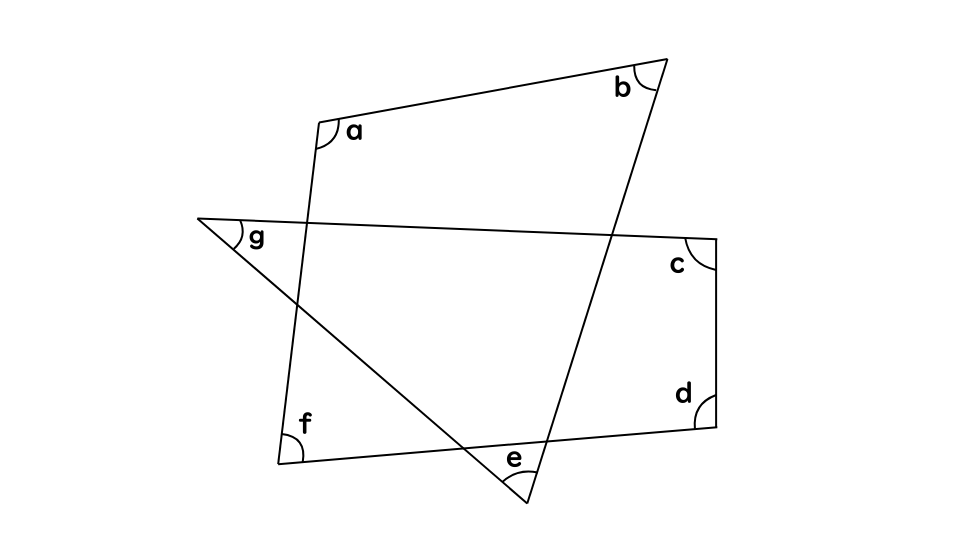
次の図において、角a~gの角度の和として、正しいのはどれか。
- 1.510°
- 2.540°
- 3.570°
- 4.600°
- 5.630°
例題2の解説・解答
今回の問題では、角が7個であるため、
(7-4)×180°
=3×180°
=540°
よって選択肢2が正解となります。
直角三角形の内接円
例題1
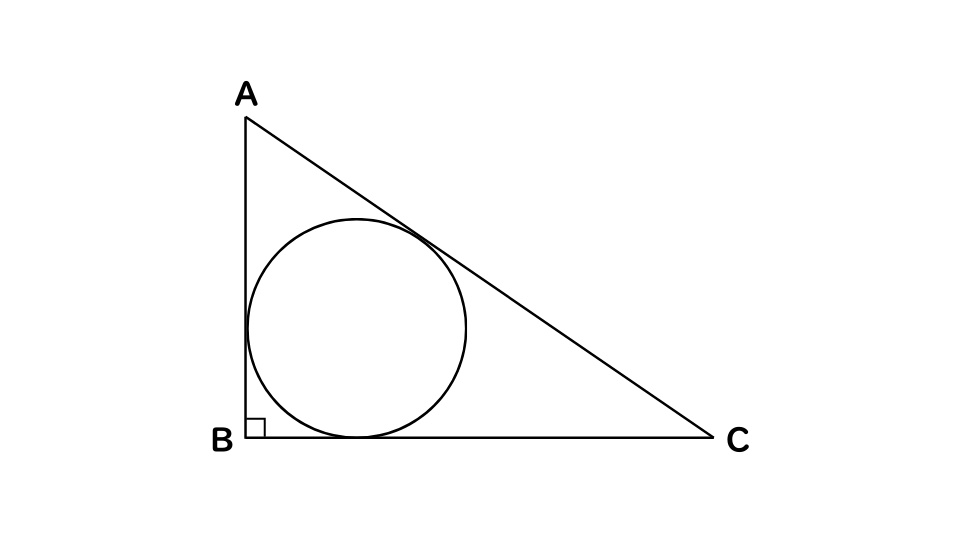
AB=3㎝、BC=4㎝、B=90°の直角三角形ABCに内接する内接円の半径は?
直角三角形の内接円とは
直角三角形の内接円とは、直角三角形に内接する円の半径や面積を求める問題です。
本来の解き方
① 三平方の定理の定理より、三角形の斜辺の長さを出す。
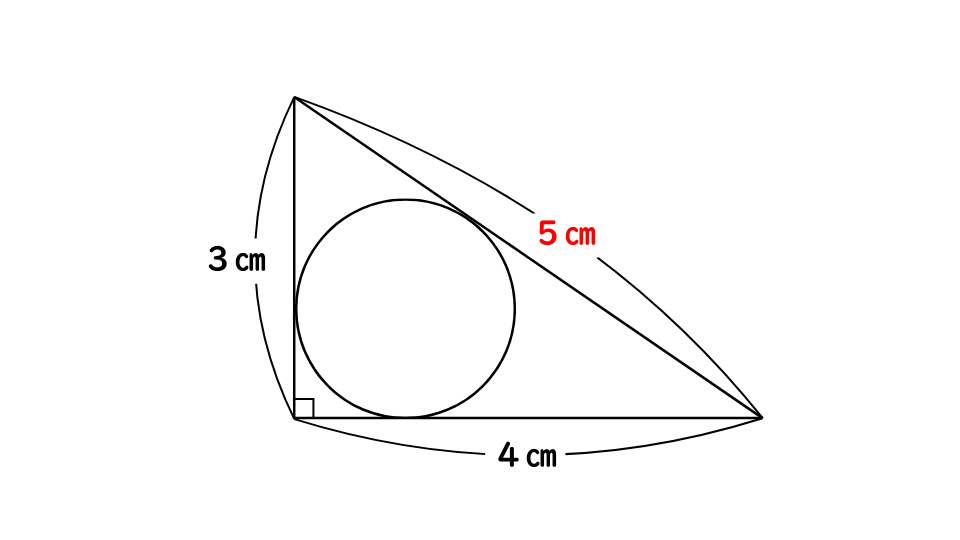
② 補助線を引いて、3つの三角形の合計の面積を出す。
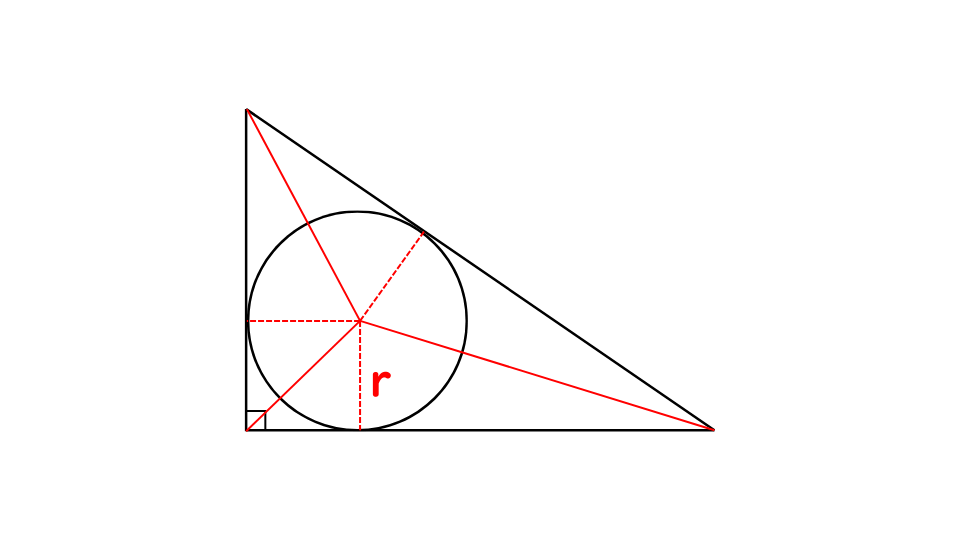
3×r×1/2+4×r×1/2+5×r×1/2=6r
③ 直角三角形の面積から半径rを求める。
3つの三角形の面積の合計と直角三角形の面積は等しい!
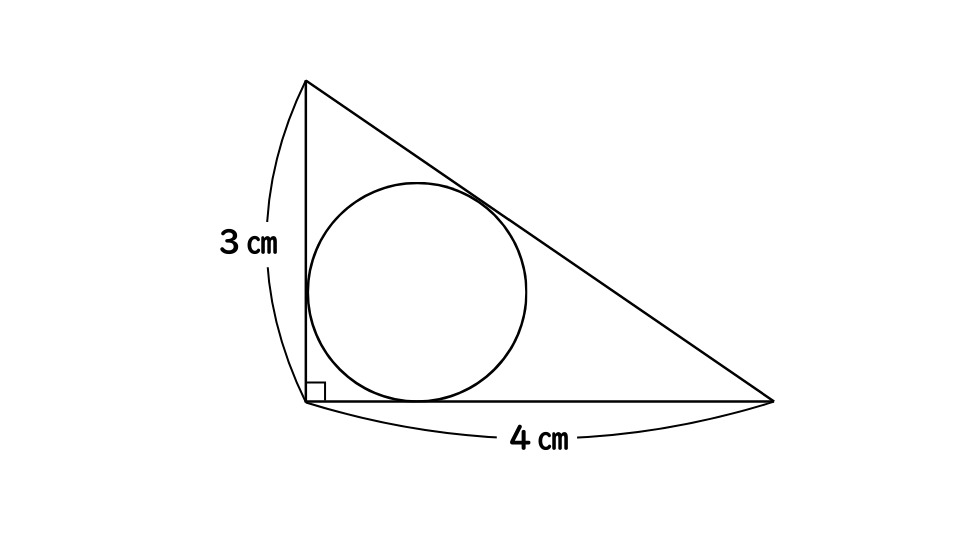
3×4×1/2=6r
6r=6
r=1
よって半径は1㎝
直角三角形の内接円の解き方
3:4:5:1
→直角三角形の辺の比が3:4:5のとき、 内接円の半径は1となる。
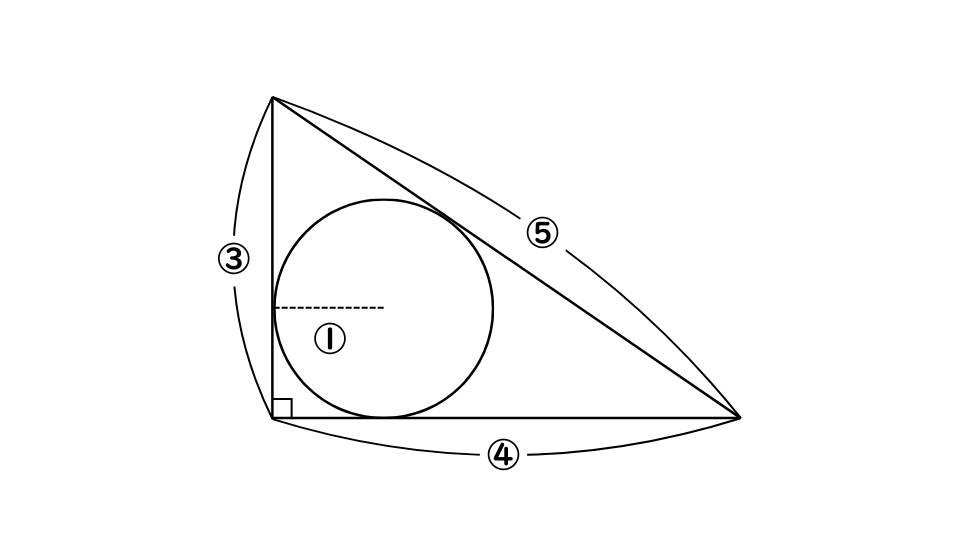
例題1の解説・解答
AB=3㎝、BC=4㎝なので、内接円の半径は1㎝となります。
例題2
次の図のように、辺ABが20㎝の直角三角形ABCに半径4㎝の円Oが内接しているとき、直角三角形ABCの面積はどれか。
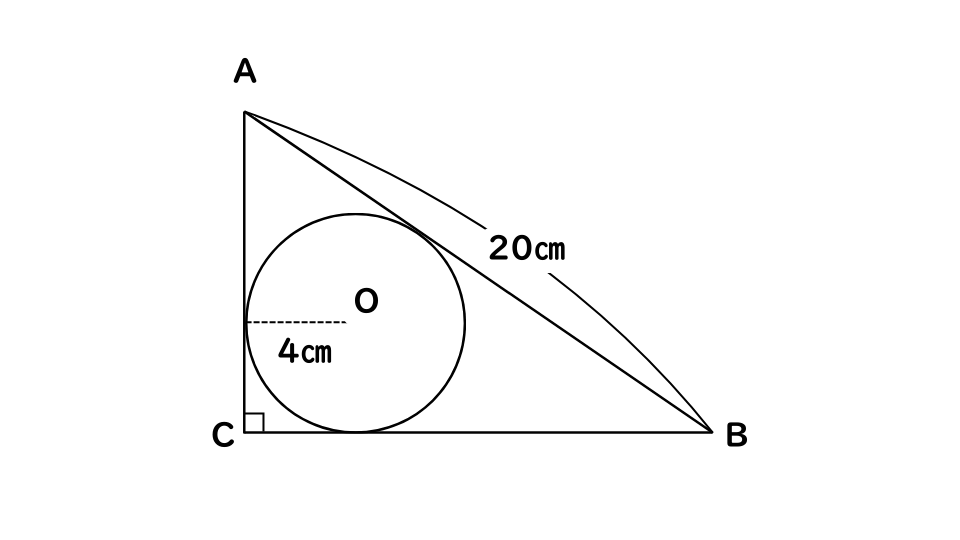
- 1.95㎠
- 2.96㎠
- 3.97㎠
- 4.98㎠
- 5.99㎠
例題2の解説・解答
3:4:5:1
→直角三角形の辺の比が3:4:5のとき、 内接円の半径は1となる。

今回の問題では、ABが20㎝、半径が4㎝より、斜辺の長さと半径の比が5:1なので、3:4:5:1より、
AC=③×4=12㎝
BC=④×4=16㎝
※今回の問題では、半径4㎝、斜辺20㎝など 比を4倍したものが長さになっている!
よってAC=12㎝、BC=16㎝であるため、
△ABCの面積は、12×16÷2=96㎠ となります。
そのため、選択肢2が正解となります。
なお、5:12:13の直角三角形の 内接円の半径は、2となります。
5:12:13:2と覚えておきましょう!
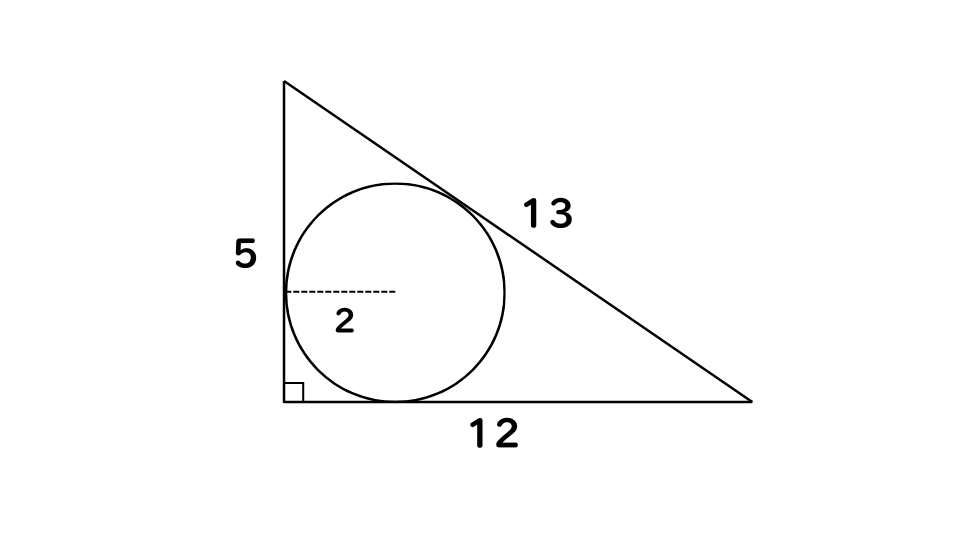
正三角形の内接円
例題1
1辺が2㎝の正三角形に内接する内接円の面積は?
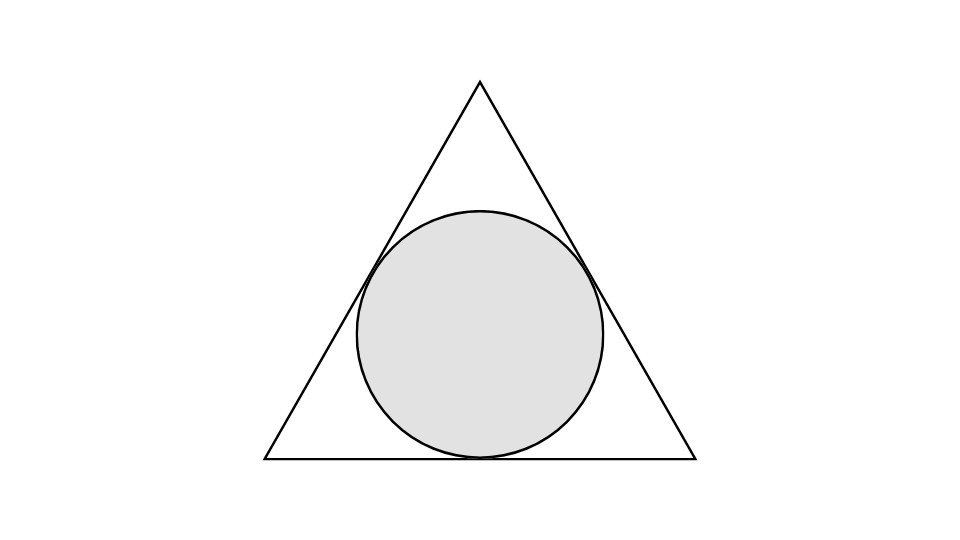
正三角形の内接円とは
正三角形の内接円とは、正三角形に内接する円の半径や面積を求める問題です。
本来の解き方
① 補助線を引く
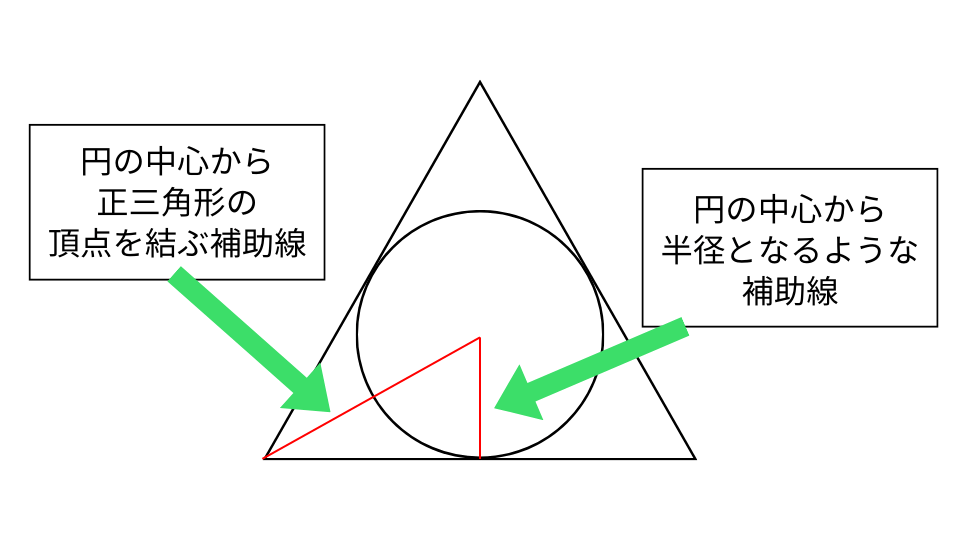
② 三平方の定理から半径を求める
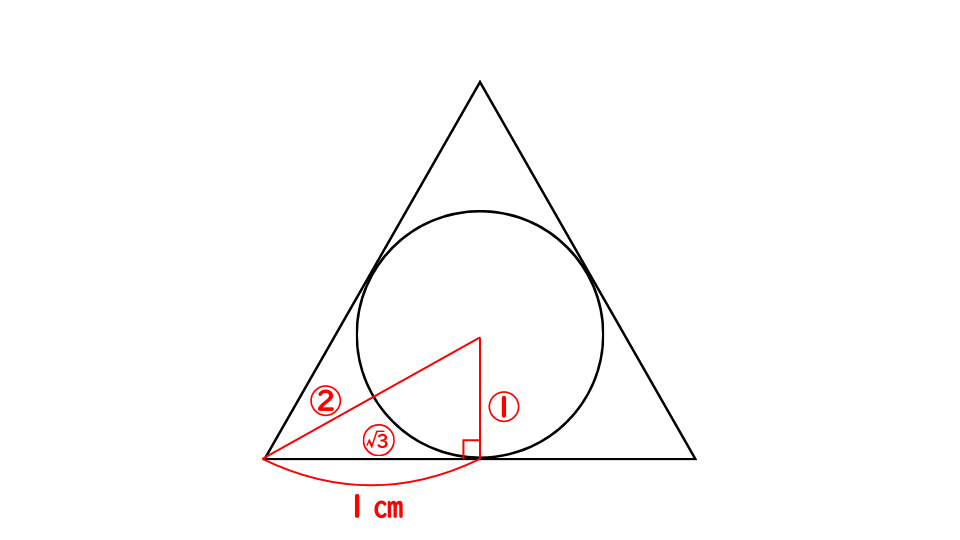
補助線を引いてできた三角形は 30度、60度、90度の直角三角形 ⇒三平方の定理が使える!
1:√3=r:1
√3r=1
r=√3/3
③ 円の面積を求める
半径×半径×πより、
√3/3×√3/3×π=1/3π㎠
正三角形の内接円の解き方
1辺×1辺×1/12π
例題1の解説・解答
今回は正三角形の1辺の長さが2㎝なので、
2×2×1/12π=1/3π㎠
例題2
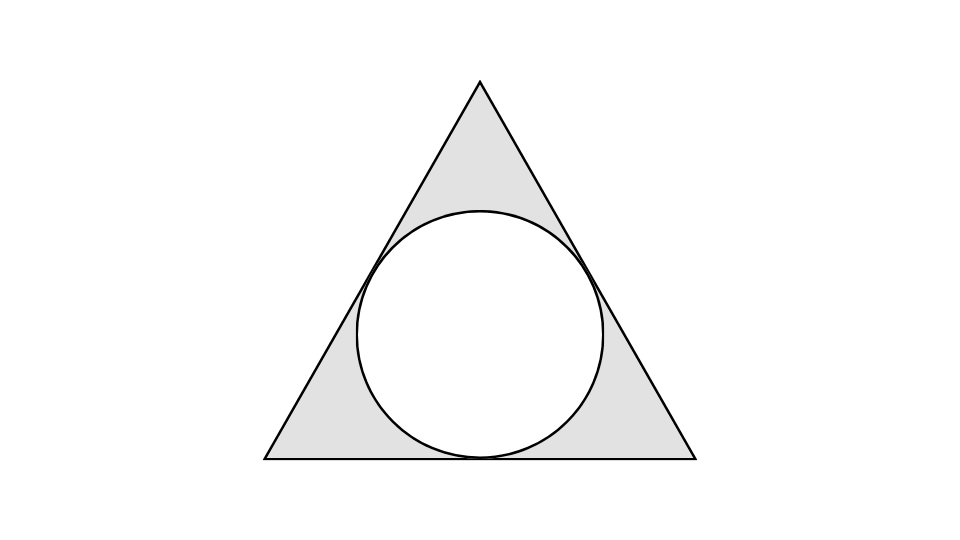
次のような一辺の長さが4aの正三角形とその内接する円で構成された灰色部の面積はどれか。
- 1.(4√3-1/3π)a²
- 2.(4√3-2/3π)a²
- 3.(4√3-π)a²
- 4.(4√3-4/3π)a²
- 5.(4√3-5/3π)a²
例題2の解説・解答
1辺×1辺×1/12π
灰色の部分は、正三角形の面積-円の面積で求めることが出来ます。
今回の問題では1辺が4aであるため、
円の面積:
1辺×1辺×1/12π
4a×4a×1/12π
=4/3πa²
灰色の面積は正三角形の面積から円の面積を引いていたものであるため、
4/3πを引いている選択肢4が正解となります。
正三角形の面積を求めなくても選択肢から正解を見つけることが出来ます。
例題3
次のような一辺の長さが2aの正三角形とその内接する円で構成された灰色部の面積はどれか。

- 1.(√3-1/3π)a²
- 2.(√3-2/3π)a²
- 3.(√3-π)a²
- 4.(√3-4/3π)a²
- 5.(√3-5/3π)a²
例題3の解説・解答
この問題も正三角形から円の面積を引いて灰色の面積を求める問題ですが、円の面積を求めるだけで、選択肢から正解を見つけることが出来ます。
今回の問題では、1辺が2aであるため、
円の面積:
1辺×1辺×1/12π
2a×2a×1/12π
=1/3πa²
よって選択肢1が正解となります。
正三角形の外接円
例題1
1辺が2㎝の正三角形に外接する外接円の面積は?
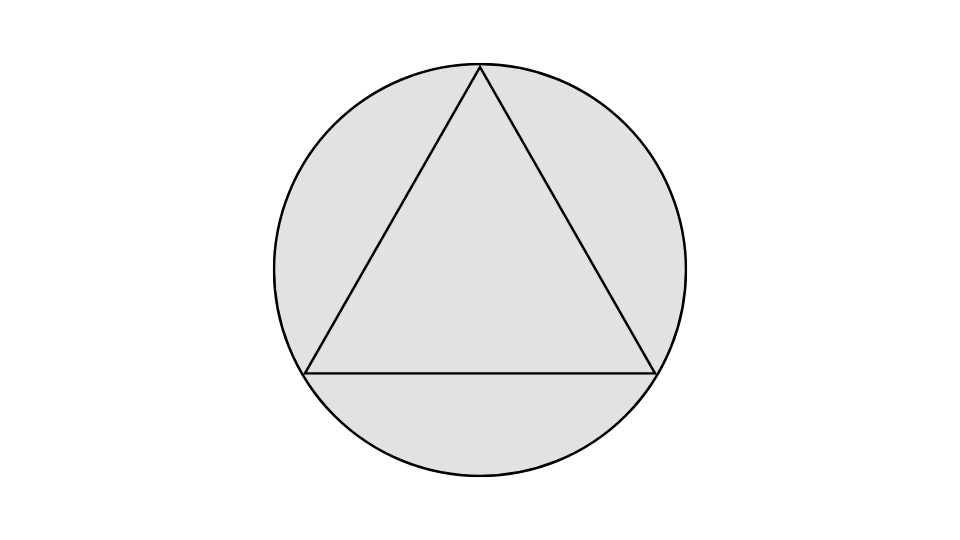
正三角形の外接円とは
正三角形の外接円とは、正三角形に外接する円の半径や面積を求める問題です。
本来の解き方
① 補助線を引く

② 三平方の定理より、半径を求める
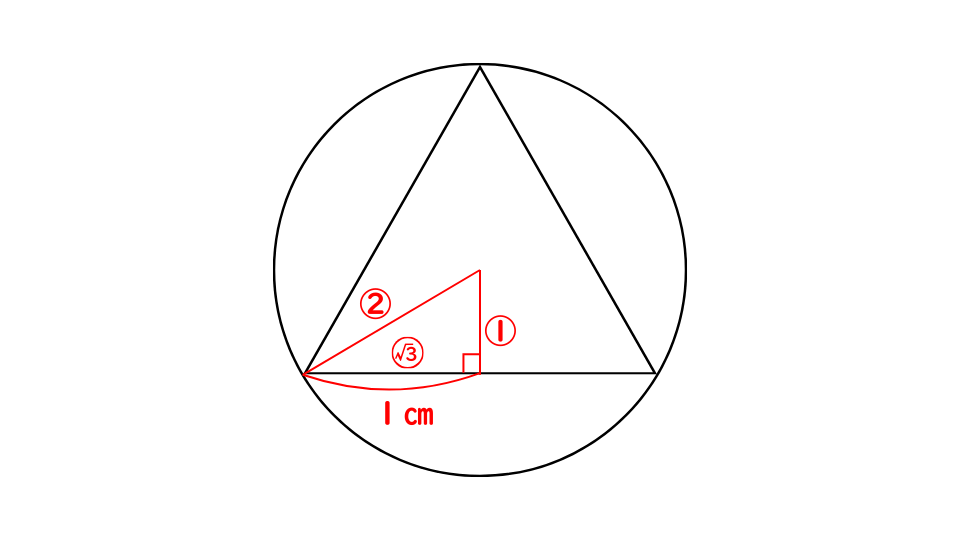
2:√3=r:1
√3r=1
r=2√3/3
③ 円の面積を求める
円の面積=半径×半径×πより、
2√3/3×2√3/3×π=4/3π㎠
正三角形の外接円の解き方
1辺×1辺×1/3π
例題1の解説・解答
今回は正三角形の1辺の長さが2㎝なので、
2×2×1/3π=4/3π㎠
例題2
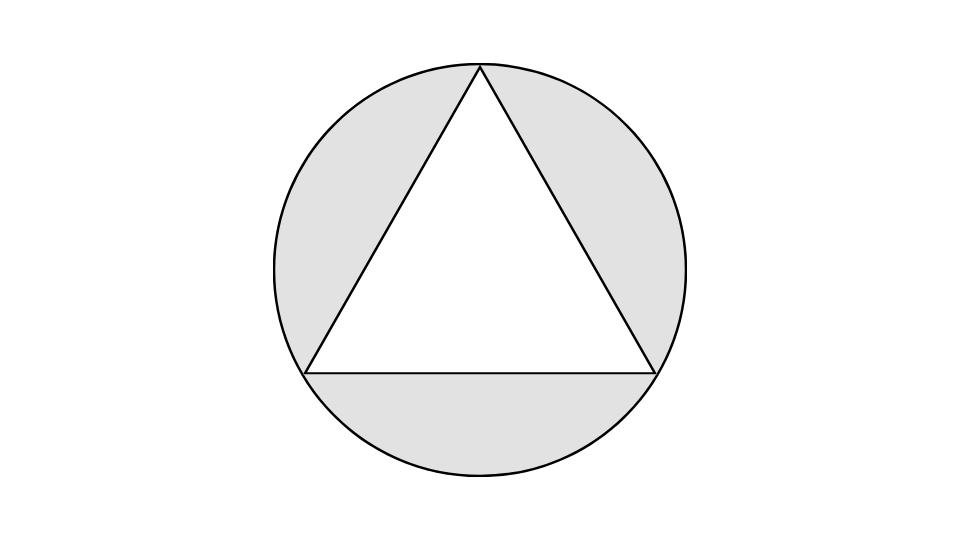
下図のような一辺の長さaの正三角形とそれに外接する円で囲まれた灰色部分の面積として、正しいのはどれか。
- 1.(π/2-√3/8)a²
- 2.(π/2-√3/4)a²
- 3.(π/3-√3/8)a²
- 4.(π/3-√3/4)a²
- 5.(π/4-√3/8)a²
例題2の解説・解答
1辺×1辺×1/3π
灰色の部分は、外接円-正三角形で求めることが出来ます。
今回の問題では1辺がaであるため、
外接円の面積:
1辺×1辺×1/3π
a×a×1/3π=π/3a²
正三角形の面積:
1辺×1辺×√3/4π
a×a×√3/4π=√3/4a²
よってπ/3a²(外接円の面積)から√3/4a²(正三角形の面積)を引いている選択肢4が正解となります。
面積まとめ
正三角形の面積:
1辺×1辺×√3/4
正三角形の内接円の面積:
1辺×1辺×1/12π
正三角形の外接円の面積:
1辺×1辺×1/3π
内12外3 なかいにがいさん で覚えましょう!
角の二等分線
例題1
下の図のように、三角形ABCがあり、この三角形と辺BCが共通で∠BDC=123°の三角形DBCがある。∠ABD=∠CBD、かつ、∠ACD=∠BCDであるとき、∠BACの角度として、正しいのはどれか。
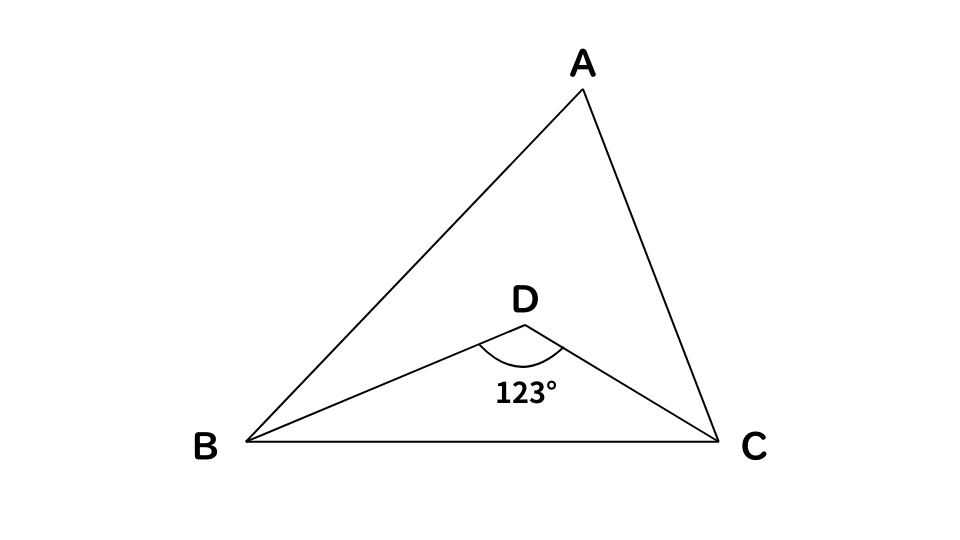
- 1.66°
- 2.69°
- 3.72°
- 4.75°
- 5.78°
本来の解き方
∠DBC=a°、∠DCB=b°、∠BAC=X°とすると、
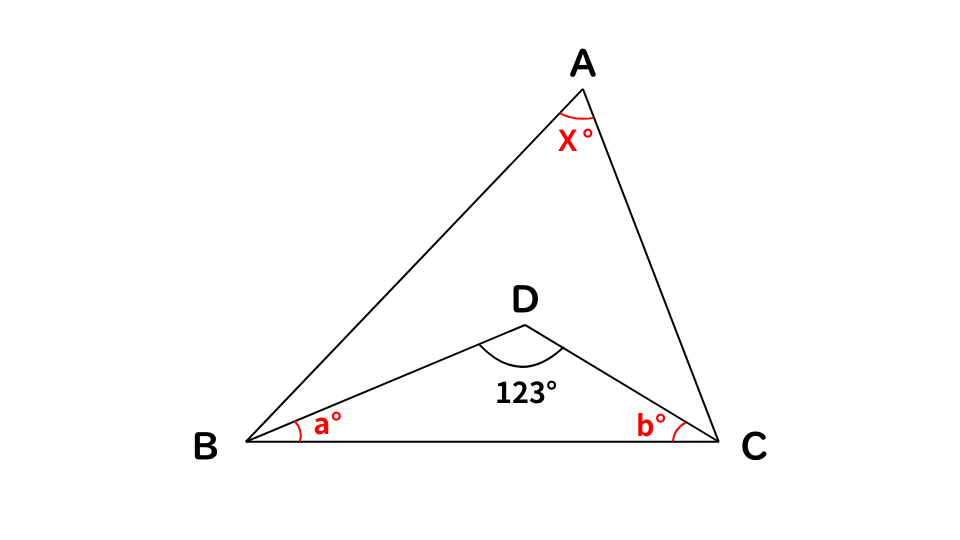
△DBCについて、三角形の内角の和は180°なので、
a+b+123°=180°
a+b=57°
問題文より、∠ABD=∠CBDであり、∠ACD=∠BCDであるため、
∠ABC=2a、∠ACB=2b
と表すことができます。
また△ABCについて、三角形の内角の和は180°なので、
2a+2b+x=180
2(a+b)+x=180
a+b=57°より、
2×77+x=180
114+x=180
x=66°
よって選択肢1が正解になります。
角の二等分線の解き方
(〇-90)×2=□
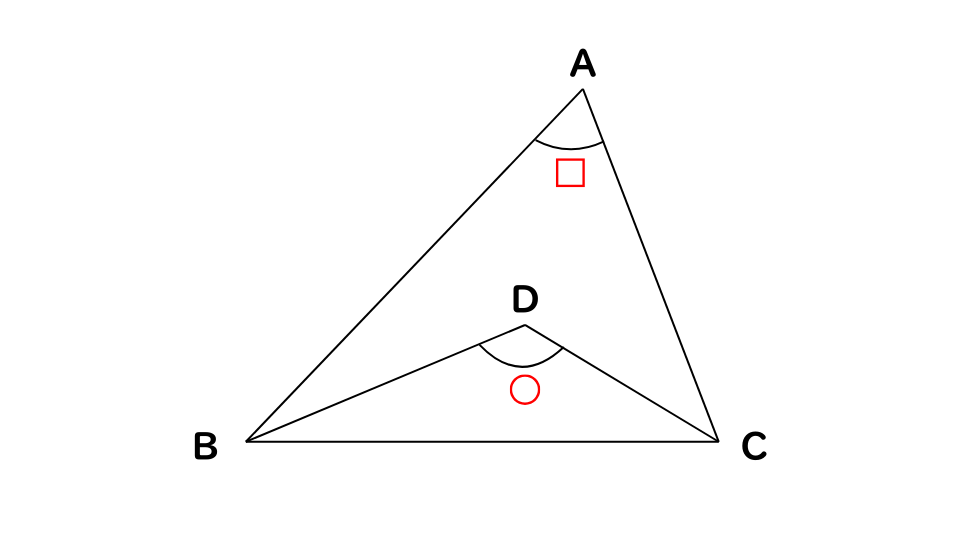
例題1の解説・解答
今回の問題では、〇=123°であるため
(123-90)×2=33×2
=66°
よって□=66°
例題2
下図のように、三角形ABCと、辺BCが共通で∠BDC=118°の三角形DBCがあり、∠ABD=∠CBD、かつ、∠ACD=∠BCDであるとき、∠BACの角度として、正しいのはどれか。
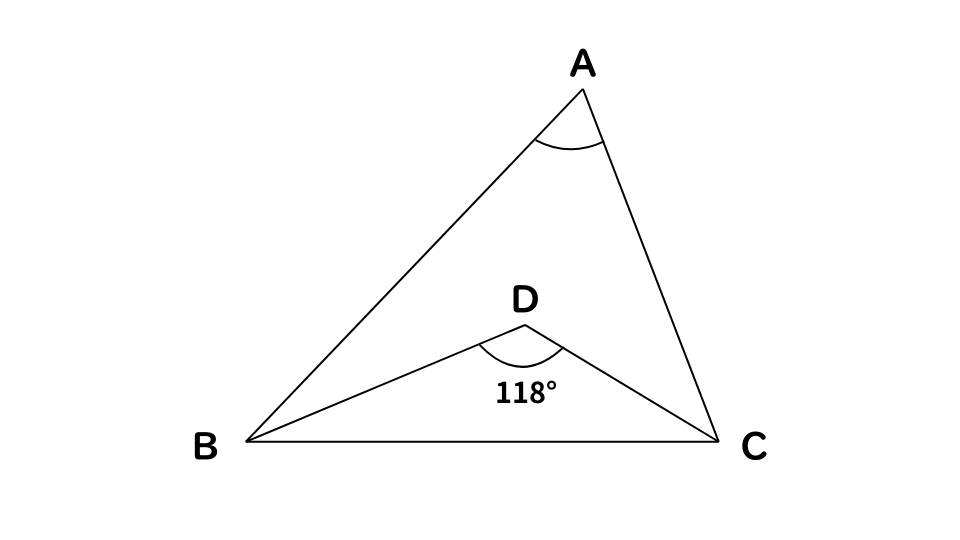
- 1.53°
- 2.56°
- 3.59°
- 4.62°
- 5.65°
例題2の解説・解答
(〇-90)×2=□

今回の問題では、〇=118°であるため
(118-90)×2=28×2
=56°
よって□=56°
したがって選択肢2が正解となります。
LINE公式にご登録頂くと、自動的に「裏技・テクニックまとめ」が送付されます。
[/box]
資料解釈
資料解釈は、選択肢を検討するうえで計算が必要となります。複雑な計算や、時間のかかる計算などがありますが、パターンとテクニックで簡略化かつ時短ができます!
計算のテクニック「文言に注目」
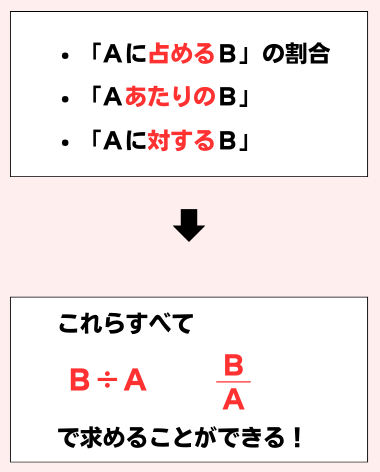
【例】

計算のテクニック「分数の大小」
分数の大小は、「分母」と「分子」に注目することで、直接計算することなく、どちらが大きいか判断することができます。分数の大小を判断するパターンは下記3つ!
(2)分子が同じで分母が異なるとき、分母が小さい方が分数自体は大きい
![]()
(3)2つの分数の分母が小さく、分子が大きい方が、分数自体は大きい
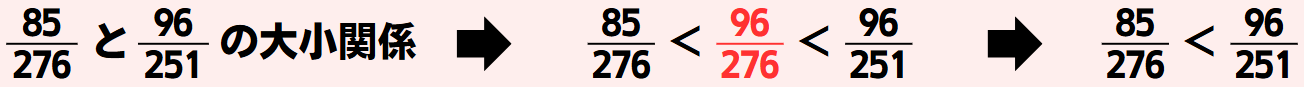
計算のテクニック かけ算の工夫
かけ算の工夫として、「%の活用」や「概算」があります。これらのテクニックを知り、短い時間の中で選択肢を検証できるようにしましょう!
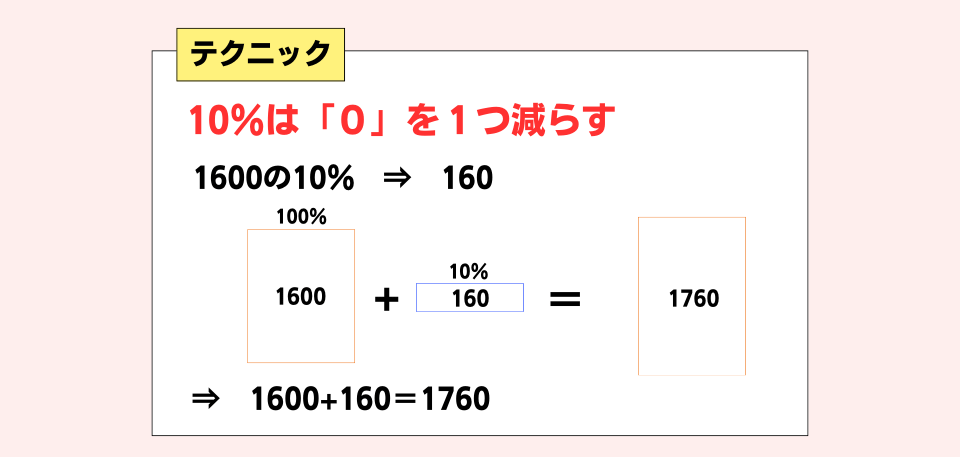
① %の活用
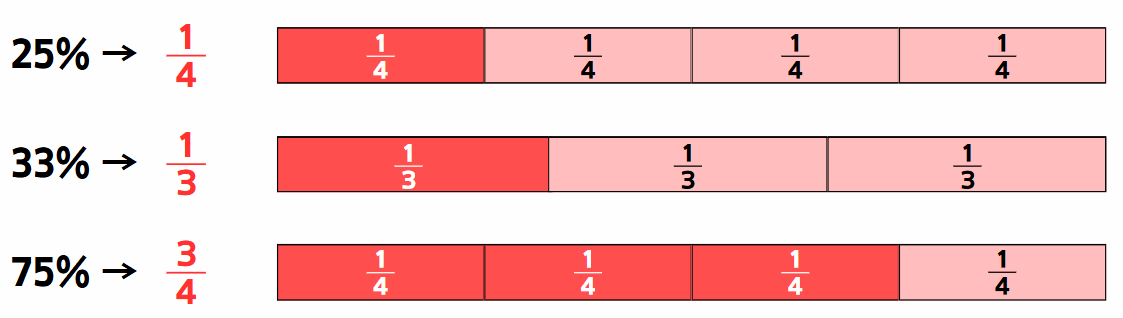
・「10%」は、「0」を1つ減らすことですぐに出すことができる。これを活用することで「20%」は「10%」×2で計算でき、「5%」は「10%」÷2で計算できる!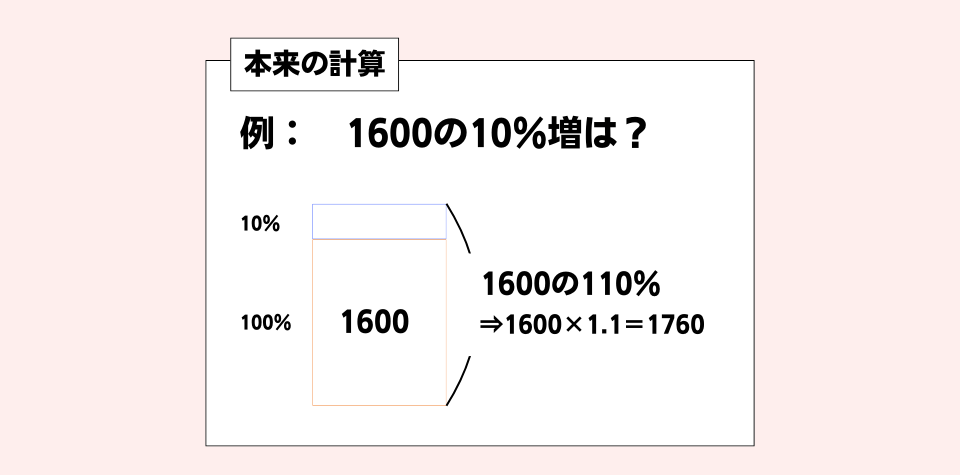
② 概算
概算とは、ざっくりとした数値で計算すること。資料解釈は、正確な数値で計算する必要はありません。ざっくりとした数値で計算することで、計算を簡略化でき、時短に繋げることができます!
・7861 ⇒ 7800
・1297 ⇒ 1300
7800÷1300=6倍
※7861÷1297≒6.06倍なので、ざっくりとした数値で計算しても答えはほとんど変わらない!
計算のテクニック 対前年増加率
① 計算のポイント
対前年増加率は、細かな計算をするとかなり複雑で時間もかかります。大きい数値がない限り(目安20%未満)、 「増減率の足し算・引き算の概数」で計算をしても、本来の計算結果とほぼ同じ数字になります!
【例】
2019年の生産量が100トンのとき、2023年の生産量は?
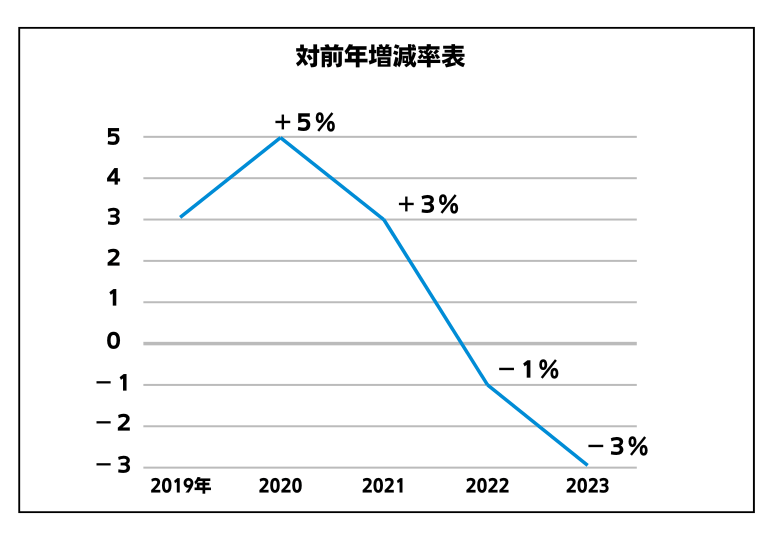
⇒100+5+3-1-3=104
(本来の計算結果とほぼ同じ数字)
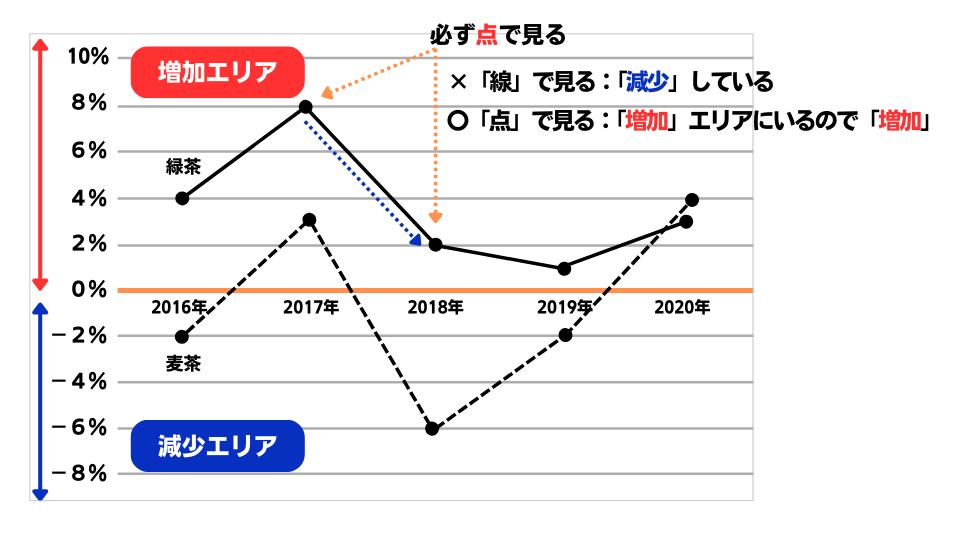
② 対前年増加率を見るときのポイント
対前年増加率の問題は、必ず「点」でグラフを見ることです。グラフにおいて、「0%」より上の点は、前年より「増加」、下の点は、前年より「減少」していることを表します。「増減率の足し算・引き算の概数」も駆使して解きましょう!
② 「0%」より上の点は「増加」、下の点は「減少」
計算のテクニック 三角グラフ
三角グラフは、見方を知ることで最も簡単に解くことができる問題です!ポイントは「見る方向に対してゆるく(鈍角)に曲がること」です。三角グラフの見方は下記の通りです。
見る方向に対してゆるく(鈍角)に曲がる
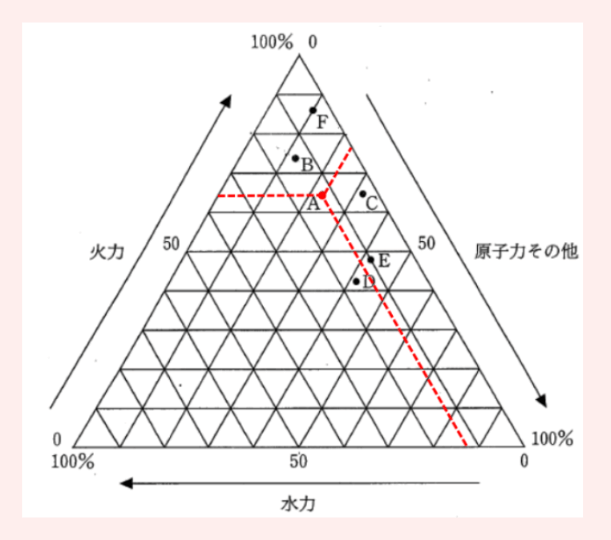
例)Aの場合
・水力:13%
・火力:65%
・原子力:22%
※各構成比を足すと必ず「100%」になる!
【例】
上記三角グラフから読み取れる構成比
| 水力 | 火力 | 原子力その他 | |
| A国 | 13% | 65% | 22% |
| B国 | 14% | 75% | 11% |
| C国 | 3% | 66% | 31% |
| D国 | 17% | 42% | 41% |
| E国 | 10% | 48% | 42% |
| F国 | 3% | 87% | 10% |
1. 火力が最も多いのは、A国である
上記の表より、火力が最も多いのは、F国であるため、誤り。
2. A国の火力発電量と、B国の水力発電量では、A国の火力発電量の方が多い。
各国の発電量はこのグラフから読み取れないため誤り。
3. 原子力その他が20%を超えているのは、4つの国である
原子力その他が20%を超えているのは、A国、C国、D国、E国の4つであるため正解
例題1
次の表から確実にいえるのはどれか。
輸送機関別国内貨物輸送量の対前年度増加率の推移
(単位 %)
| 区分 | 平成24年度 | 25 | 26 | 27 | 28 |
| 鉄道 | 6.2 | 4.2 | △1.5 | △0.5 | 2.0 |
| 自動車 | △2.9 | △0.5 | △0.7 | △0.6 | 2.1 |
| 内航海運 | 1.4 | 3.4 | △2.4 | △1.0 | △0.3 |
| 航空 | 1.8 | 5.7 | 2.4 | △1.0 | △2.2 |
(注) △は、マイナスを示す。
- 1.平成28年度の自動車の国内貨物輸送量は、平成24年度のそれの1.1倍を上回っている。
- 2.平成24年度の航空の国内貨物輸送量を100としたときの平成27年度のそれの指数は、110を下回っている。
- 3.表中の各年度のうち、鉄道の国内貨物輸送量が最も多いのは、平成24年度である。
- 4.平成26年度において、自動車の国内貨物輸送量の対前年度減少量は、内航海運の国内貨物輸送量のそれを下回っている。
- 5.鉄道の国内貨物輸送量の平成25年度に対する平成27年度の減少率は、内航海運の国内貨物輸送量のそれより大きい。
本来の解き方
例えば、各年の鉄道の輸送量を求める際には、以下のように計算します。
平成23年度の輸送量を100とすると、
平成24年度:
6.2%増加しているので、
100×1.062=106.2
平成25年度:
106.2×1.042=110.6604
平成26年度:
110.6604×0.985=109.000494
平成27年度:
109.000494×0.995=……
このように、計算がとても複雑になってしまって大変…
そこで解き方のポイント!
輸送量の求め方
例えば、鉄道であれば、
平成23年度の輸送量を100とすると、
平成24年:
100+6.2=106.2(100+24年度増加率)
平成25年:
106.2+4.2=110.4(106.2+25年度増加率)
平成26年:
110.4-1.5=108.9(26年度はマイナスなので引き算をします!)
平成27年:
108.9-0.5=108.4
平成28年:
108.4+2=110.4
本来の解き方のような複雑な掛け算をしなくとも、簡単に輸送量を求めることができます。
例題1の解説・解答
1.平成24年度の自動車の国内貨物輸送量を100とすると、1.1倍は110となります。
平成28年度は、
100-0.5-0.7-0.6+2.1=100.3
よって、1.1倍を上回っていないため、誤り。
2.平成24年度の航空の国内貨物輸送量を100とすると、
平成27年度は、
100+5.7+2.4-1.0=107.1
よって、110を下回っており、妥当。
3.平成23年度の鉄道の国内貨物輸送量を100とすると、
平成24年度は、
100+6.2=106.2
平成25年度は、
100+6.2+4.2=110.4
よって、平成25年度の方が多く、平成24年度が最も多いとは言えないため、誤り。
4.表中からは、自動車及び内航海運の輸送量は分からず、平成26年度における減少量を比較することができないため、誤り。
5.それぞれの平成25年度に対する平成27年度の減少率は、
鉄道:
-1.5-0.5=-2
内航海運:
-2.4-1.0=-3.4
よって、減少率は内航海運の方が大きく、鉄道の方が大きいとは言えないため、誤り。
よって選択肢2が正解となります。
例題2
次の図から正しくいえるものはどれか。
わが国における水産物の缶詰4種の生産量の対前年増加率の推移
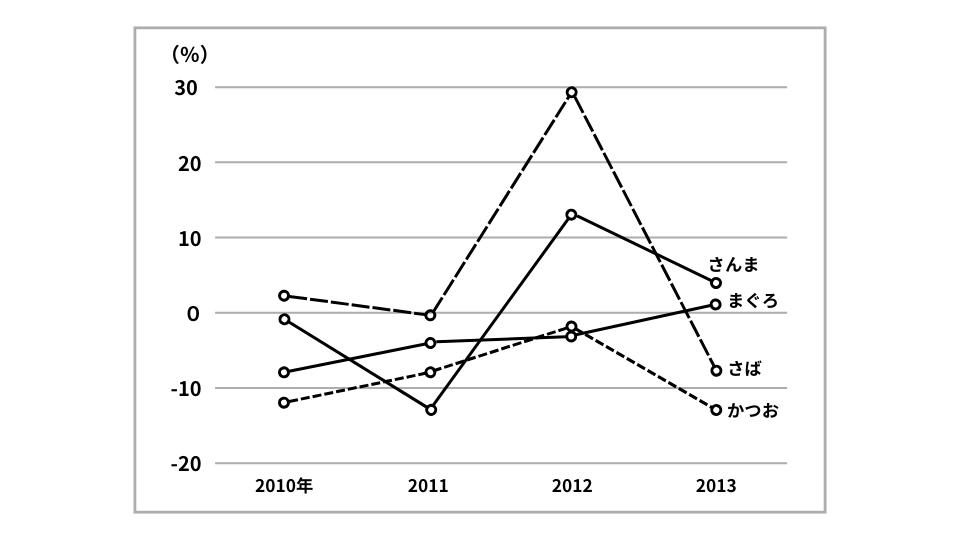
- 1.2010年から2012年までのうち、まぐろの缶詰の生産量が最も多いのは2012年であり、最も少ないのは2010年である。
- 2.2011年についてみると、4種の缶詰のうち、生産量が前年に比べて減少したのはさばの缶詰とさんまの缶詰だけである。
- 3.かつおの缶詰の生産量についてみると、2010年を100としたとき、2012年の指数は80を下回っている。
- 4.さばの缶詰の生産量についてみると、2011年から2013年までの3か年の1年あたりの平均の生産量は2010年の生産量を上回っている。
- 5.さんまの缶詰の生産量の対前年増加量についてみると、2013年は2012年を上回っている。
例題2の解説・解答
資料から対前年増加率を読み取ると、おおよそ以下の通りとなります。
| 2010 | 2011 | 2012 | 2013 | |
| さんま | -0.8 | -13 | 13 | 4 |
| まぐろ | -8 | -4 | -3 | 1 |
| さば | 2 | -0.5 | 29 | -8 |
| かつお | -12 | -8 | -2 | -13 |
対前年増加率の概数は、大きい数値がない限り(目安20%未満)、足し算・引き算で考えることができます。
今回の問題では、さばの2012年が29と20%を超えているが、2010、2011での増減に幅があまりないため、大きな誤差は出ず、足し算・引き算で求めことができます。
1.2009年のまぐろの缶詰の生産量を100とすると、それぞれの生産量は、
2010年:
100-8=92
2011年:
92-4=88
よって、2010年より2011年の方が少なく、2010年が最も少ないとは言えないため、誤り。
2.2011年において、4種すべて前年比マイナスとなっています。
よって、さばとさんまだけとはいえず、誤り。
3.2010年のかつおの缶詰の生産量を100とすると、2012年は、
100-8-2=90
よって、80を下回っておらず、誤り。
4.3か年における生産量の1年あたりの平均は、3か年の生産量の合計÷3で求めることができます。
2010年を100とすると、
2011年:
100-0.5=99.5
2012年:
99.5+29=128.5
2013年:
128.5-8=120.5
(99.5+128.5+120.5)÷3≒116.167
よって、2010年の生産量を上回っているため、妥当。
5.対前年増加量は、そのまま対前年増加率の比較で検討することができます。
2012年:13
2013年:4
よって、2013年は2012年を上回っておらず、誤り。
よって選択肢4が正解となります。
総まとめ
公式LINEにご登録頂くと、自動的に「裏技・テクニックまとめ」が送付されます。
YouTube
動画による解説はこちらをチェックしてください↓
数的処理フルパック

- 数的をゼロからしっかり学びたい
- 数的が苦手でもう一度基礎から学びたい
- 応用問題が解けるようになりたい
- 実際の過去問で実戦力を身に付けたい
こんな方にオススメしています。
![公務員のライト[試験情報データベース]](https://senseikoumuin.com/wp-content/uploads/2022/12/cropped-logo-color-2.png)









-6-485x273.jpg)




② 何本の線が交わっているかを数える
③ 「②の本数が奇数」の交差点が2か所または0か所のときに一筆書きができる